Het probleem van verhinderde vervorming is dat dit (trek)span- ningen veroorzaakt. Zodra deze span- ningen groter zijn dan de treksterkte van het beton, k an dat leiden tot scheurvorming. Vervormingen kunnen worden veroor - zaakt door krimp ( ?cs) of temperatuurveran- dering ( ?cT). Krimp van beton geeft een opge- legde vervorming van alleen het beton. Bij een opg elegde temperatuurdaling willen zo - wel het beton als het wapeningsstaal verkor- ten. Navolgend wordt de vraag betantwoord of dat een essentieel verschil in de uitkom - sten voor de scheurwijdteberekening geeft. Beide v ormen van opgelegde vervorming worden in dit artikel afzonderlijk besproken. Randvoorwaarden In betonverhardingen treedt axiale vervor- ming op die wordt verhinderd door de wrij- ving met de ondergrond. Ter vereenvoudi- ging is er in dit artikel voor gekozen uit te gaan van verhindering van de vervorming aan de uiteinden van de verharding. Daarnaast treden niet-lineaire vervor- mingen op over de dikte van de betonver- harding als gevolg van variaties in de tempe- ratuur en relatieve vochtigheid aan het betonoppervlak. Ter vereenvoudiging zijn de niet-lineaire rekgradiënten buiten beschou- wing gelaten. Bovengenoemde randvoorwaarden kunnen als volgt worden samengevat: de verharding is aan de beide uiteinden axiaal oneindig stijf gefixeerd, waardoor de opgelegde vervormingen geheel worden ver- hinderd (fig. 1); uitsluitend gelijkmatige opgelegde rekken, geen gradiënten. Een veel toegepaste methode is om de mate van verhindering uit te drukken in een DR.IR. GUSTAAF BOUQUETauteur Scheurvorming onder invloed van afkoeling en krimp Betonconstructies kunnen worden blootgesteld aan de opgelegde vervormingen. Vaak worden die vervormingen verhinderd. Dat geldt onder meer voor voegloze (elastisch ondersteunde) bedrijfsvloeren en betonverhardingen (betonwegen) in doorgaand-gewapend beton (DGB). Welke krachten en (staal)spannigen treden er op in een dergelijke verharding? Verschil in uitkomsten scheurwijdteberekening bij verhinderde opgelegde vervorming voor een doorgaand-gewapende betonverharding door afkoeling en door krimp 46? CEMENT 5 20 21 Figuur 3 Optredende spanning in beton ( c\f0) en het betonstaa\b ( s\f0) in de ongescheurde fase ( c < cr) onder inv\boed van krimp in het beton. L0 A
? ? N c < N max betonspanning: 0 c < cr staalspanning: s = 0 0 N c < N max opgelegde rek beton: 0 ? ??? ? ??? R R graad van verhindering. Met deze graad van verhindering wordt de relatie gelegd tussen de opgelegde vervorming en de rek die de (trek)spanning tot gevolg heeft: ?c? = - ?R?cX (1) w aarin: ?cX = opg elegde vervorming (krimp: ?cs; temperatuur: ?cT) [m/m] ?R = gr aad van verhindering [-], 0 ? ?R ? 1 ?c? = spanningg evende rek [m/m], ?c? ? 0 bij krimp en afkoeling Bij een betonverharding in doorgaand-ge- wapend beton ontstaat er bij een zekere afstand van de uiteinden een situatie waar- bij vervormingen door de grondwrijving volledig worden verhinderd ( ?R = 1). Vervormingen door krimp Voor de analyse van het gedrag van gewapend beton onder invloed van krimp beschouwen we een verharding met lengte L 0 die aan beide uiteinden is ingeklemd (fig. 1). Ongescheurde fase? Het beton blijft onge- scheurd zolang de spanninggevende rek ( ?c ?) kleiner is dan de scheurrek van op trek belast beton ( ?cr). De trekspanning in het beton is dan kleiner dan het beton met scheurspan - ning ?cr. Omdat de verharding onvervorm - baar is ingeklemd, blijft het betonstaal in de ong escheurde fase spanningsloos. Dit terwijl de betonspanning de scheurrek nadert. De trekkracht N c in het beton bereikt juist voor het moment van scheuren een maximale waarde: N cs,max = ?cr Ac (2) w aarin: ?cr = scheur spanning beton [N/mm²] A c = door snede beton [mm²], (beton- door snede exclusief doorsnede betonstaal) Eerste scheur? Bij verdere toename van de krimp zal er ergens in het element de eerste scheur ontstaan. Ter plaatse van de scheur wordt de scheurkracht van het beton ( ?cr Ac) door het betonstaal overgenomen, met als gevolg staaltrekspanningen die de grootste waarde ( ?s2) ter plaatse van de scheur berei- ken. Om nu aan de randvoorwaarde te kun- nen voldoen dat de gesommeerde rekken in het staal over de hele lengte van het element nul moeten zijn, moet de staaltrekspanning ter plaatse van de scheur worden gecompen - seerd door een, constant veronderstelde, staaldrukspanning ( ?s1) in de ongescheurde zones 1 (fig. 2). Aan weerszijden van de scheur neemt de betontrekspanning over de overdrachts- lengte (l t) weer toe tot een betontrekspan- ning ( ?s1). De over de storingszone (lengte: 2l t) optredende verlenging van het beton en de wijdte van de scheur (w) in het beton, wor- den gecombineerd tot een fictieve zone waarover de betonspanning 0 is veronder- steld (fig. 2). De lengte van die zone is: 2(1/2l t) + w ? l t (3) w aarin: w = scheurwijdte [ mm] l t = o verdrachtslengte [mm] 1 Optredende spanning in beton (? c,0) en het betonstaal (? s,0) in de ongescheurde fase (? cs < ? cr) onder invloed van krimp in het beton GEDEELTELIJKE VERHINDERING In dit artikel is de verhindering van de opgelegde vervormingen geschemati- seerd door inklemmingen aan beide uiteinden van de gewapend betonnen verharding. Dit is in feite een bijzonder geval met volledige verhindering van de optredende vervormingen (trans- latie en rotatie). Voor het meer alge- mene geval waarbij de optredende vervormingen gedeeltelijk worden verhinderd, wordt verwezen naar de studie van Falkner [1], waarbij de verhindering van de temperatuurver- vormingen zijn geschematiseerd met rotatie- en translatieveren aan de uiteinden van het betonelement. 1 CEMENT 5 2021 ?47 Toelichting: N cs,max = maximale normaal\fracht in ongescheurde situatie [\b] N cr,1 = normaal\fracht na het ontstaan van de eerste scheur [\b]     \b
      \b
      \b
  l t = overdrachtslengte [mm] F iguur 4 Aan de uiteinden inge\flemde betonverharding onder invloed van een opgelegde verhinderde \frimp. Situatie na ontstaan van de eerste scheur L0 A
? Nc s,max Ncs,max N

?U? N

?U?
?
}
v
 ?
?
}
v
 ?
?
}
v
 ? l
? w lt c1 s1 s2 s2 s1 betonspanningen staalspanningen geschematiseerde st aalspanningen opgelegde rek beton: c = cr lt Deze aanpak voor de berekening van de op- tredende krachten en spanningen in gewa- pend beton onder invloed van de krimp, is qua randvoorwaarden en schematisering gebaseerd op de methode zoals omschreven in [2]. Opvolgende scheuren? De eerste scheur is ontstaan toen de spanninggevende rek ( ?c ?) gelijk was aan de rek bij scheuren van het beton ( ?cr). Daarbij is de maximale trek - kracht N cs,max bereikt. Direct na het optre- den van scheurvorming neemt de axiale rekstijfheid van de betonverharding af. Omdat de grootte van de opgelegde vervor- ming niet verandert, valt de trekkracht terug naar een lagere waarde (N cr,1). Bij een verdere toename van de spanninggevende rek ontstaat de tweede scheur als de maximale trekkracht (N cs,max ) weer wordt bereikt. Zo ontstaan er bij een steeds groter wordende spanninggevende rek steeds meer scheuren. In figuur 3 is de gescheurde situatie ten gevolge van krimp, met de staal- en betonspanningen, schematisch weergegeven bij meerdere scheuren. Verondersteld is dat de afstanden tussen de scheuren groter zijn dan tweemaal de overdrachtslengte. 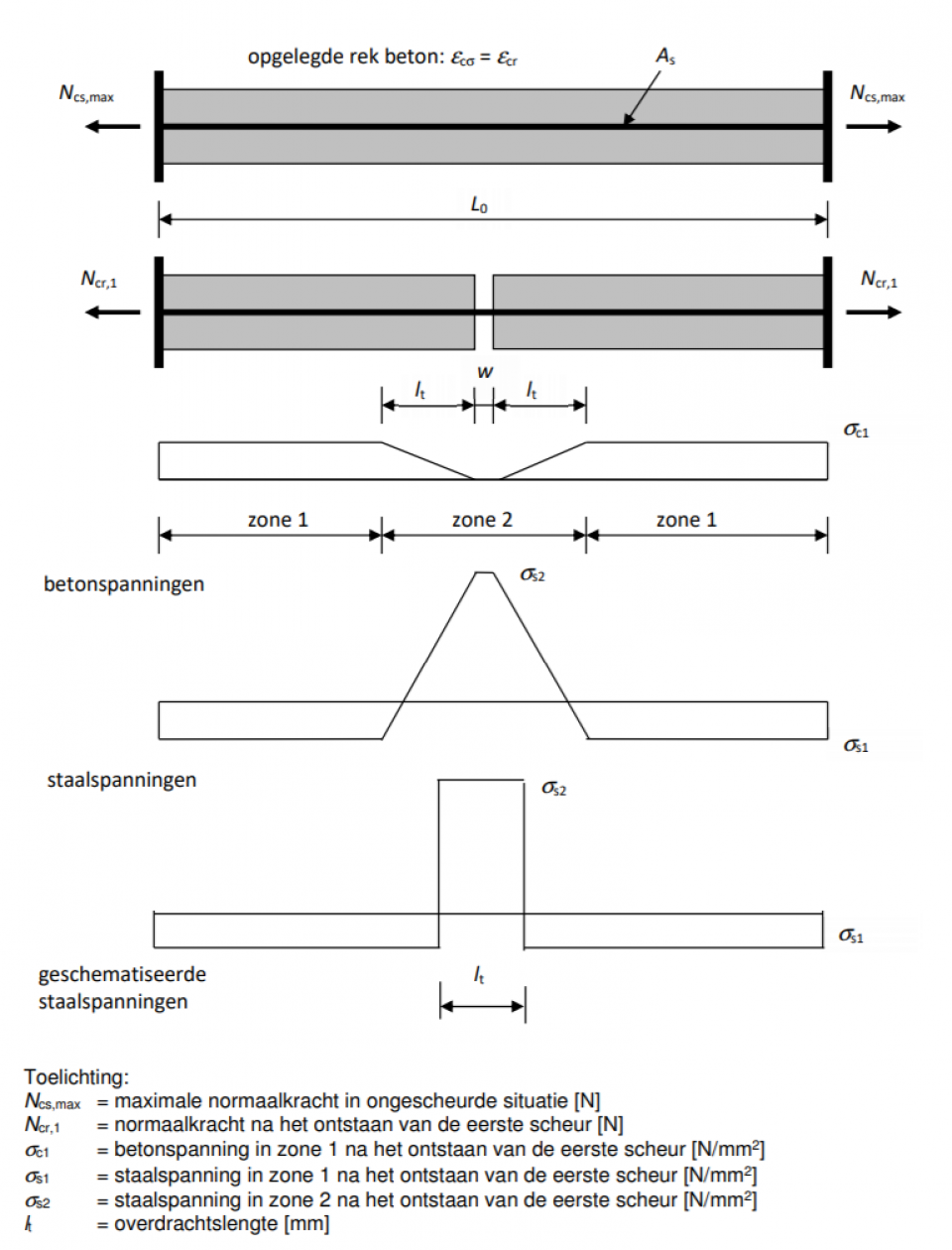Vervormingen door krimp Voor de opgelegde rek ten gevolge van een temperatuurverandering geldt: ?cT = ?cT (T - T 0) (4) 2 Aan de uiteinden ingeklemde betonverharding onder invloed van een opgelegde verhinderde krimp. Situatie na ontstaan van de eerste scheur Ter plaatse van de eerste scheur wordt de scheur- kracht van het beton door het betonstaal over- genomen met als gevolg staal- trekspanningen 2 48? CEMENT 5 20 21 Figuur 5 Geschematiseerde verdeling van de \feton- en staalspanningen in de ongescheurde \bones ( c1 en s1) en de staalspanning in de scheuren ( s2) F iguur 6a Optredende krachten tijdens de krimp. Zonder relaxatie. L 0 = 25 m, N cs,max = 495,8 kN, \fij c = 3,40 10 -6 m/m is N cr = 359,6 kN 340 3 60 380 400 420 440 460 480 500 0,0E+00 5,0E-05 1,0E-04 1,5E-04 2,0E-04 2,5E-04 3,0E-04 3,5E-04 4,0E-04 kracht [kN ] rek [m/m] krimp L= 25 m zonder relaxatie s/2 s1 s2 s2 s2 sl? s s lt l
? c1 + + + + + + - - - - L? N N + + + - s2 s lt 3 waarin: ?cT = opg elegde rek als gevolg van de temper atuurverandering (T - T 0) [m/m] ?cT = lineair e uitzettingscoëfficiënt beton [ m/mK]; ?cT = 10 · 10 -6 m/mK T = actuele betontemper atuur [K] T 0 = r eferentietemperatuur waarbij het beton spanningsloos is [K] Bij toename van de spanninggevende rek ( ?c?, zie vgl. 1), als gevolg van de opgelegde rek door temperatuurdaling ( ?cT, zie vgl. 4), neemt de trekkracht toe tot de maximale waarde: N T,max = ?cr Ac (1 + ?e ?) (5) waarin: N T,max = ma ximale kracht voor ontstaan v an een scheur [N]; ?cr = scheur spanning beton [N/mm²] A c = door snede beton [mm²], (beton door snede exclusief doorsnede betonstaal) ?e = verhouding elasticiteitsmoduli staal/ beton [MPa/MPa], ?e = E s/Ec ? = w apeningsfractie [mm²/mm²], ? = A s/Ac Het essentiële verschil tussen de maximale trekkracht als gevolg van krimp (N cs,max in vgl. 2) en de maximale trekkracht bij verla- ging van temperatuur (N T,max in vgl. 5) is dat er bij krimp geen rek in het betonstaal optreedt, terwijl bij verlaging van de tempe- ratuur zowel het beton als het betonstaal onderhevig zijn aan een opgelegde rek. Scheurwijdte bij verhinderde vervorming In het geval van opgelegde vervormingen ontstaat vrijwel altijd een onvoltooid scheu- renpatroon. De gemiddelde scheurwijdte kan in dat geval worden berekend met het 'TU Delft trekstaafmodel' [3] met het alge- mene toetsingscriterium voor de scheur- wijdte bij een onvoltooid scheurenpatroon: w toets = w mo ?s ?? ? w eis ( 6) waarin: w toets = toets waarde van de scheurwijdte [mm] w mo = g emiddelde scheurwijdte bij een on voltooid scheurenpatroon [mm] w eis = het g eldende vereiste scheur- wijdtecriterium bij een bepaalde milieuklasse [ mm] ?s = f actor voor optredende spreiding [-], on voltooid scheurenpatroon: ?s = 1,3 ?? = f actor voor langeduur/wisselbelas- ting b ij ?s,cr ? 295 N/mm² [-]: ?? = 1,3 Hierbij geldt voor de gemiddelde scheurwijdte bij een onvoltooid scheurenpatroon [3]: 3 Geschematiseerde verdeling van de beton- en staalspanningen in de ongescheurde zones (? c1 en ? s1) en de staalspanning in de scheuren (? s2) CEMENT 5 2021 ?49 () (), ck,cube 5 s 0 ,8 mo s cr s,cr e cr Ø0 , 4 2 8 w E f ? ??? = ? ??? ? ? +? ???? ? (7) w aarin: w mo = g emiddelde scheurwijdte bij een on voltooid scheurenpatroon [mm] Ø = diameter betonstaal [mm] f ck,cube = k arakeristieke kubusdruksterkte [N/mm²] E s = elasticiteitsmodulus betonstaal, Es = 200000 N/mm² ?s,cr = staalspanning in de scheur [N /mm²], (zie vgl. 12 en 13) ?cr = scheur spanning beton [N/mm²] ?e = verhouding elasticiteitsmoduli staal/ beton [MPa/MPa], ?e = E s / E c Relaxatie Het effect van relaxatie op het scheurgedrag als gevolg van krimp en temperatuurverla- ging wordt in rekening gebracht door mid- del van het een gereduceerde 'effectieve' elasticiteitsmodulus van beton: E c? = ? Ecm (8) met de r elaxatie coëfficiënt [4]: () () , ck,cube 5 s 0 ,8 mo s cr s,cr e cr Ø0 , 4 2 8 w E f ? ??? = ? ??? ? ? +? ???? ? 1 1 0, 8 = + cr s,cr = ()cr s,cr e1 =+ (9) w aarin: ? = r elaxatiecoëfficiënt [-] ? = kruipcoëfficiënt [-] E c? = eff ectieve elasticiteitsmodulus beton [N /mm²] E cm = secant elasticiteitsmodulus beton [N/mm²] Rekenvoorbeeld Een en ander wordt toegelicht met een reken - voorbeeld. Hierbij is uitgegaan van een beton - verharding in doorgaand-gewapend beton met een dikte van 250 mm en een wapenings- percentage van 0,75%. De invloed van de lengte van de beton- verharding is onderzocht met twee lengten, te weten 25 m en 100 m. De uitgangspunten Het verschil tus- sen de maximale trekkracht als gevolg van krimp en temperatuur- verlaging is dat er bij krimp geen rek in het beton - staal optreedt Tabel 2?Berekende grootheden en parameters omschrijving symbool grootte kruipcoëfficiënt ?1,91 relaxatiecoëfficient ?0,4 secant elasticiteitsmodulus beton (zonder/met relaxatie) E cm 34077 / 13480 N/mm² opgelegde vervorming door krimp ? cs - 400 × 10 -6 m /m opgelegde vervorming door 20 °C afkoeling ? cT - 200 × 10 -6 m /m gem. 28-daagse korteduur treksterkte beton f ctm,0 3,33 N/mm² scheurspanning beton ? cr 2,0 N/mm² scheurrek beton (zonder/met relaxatie) ? cr 58,6 × 10 -6 / 148,2×10 -6 m /m doorsnede betonstaal per m' A s 1870 mm²/m' wapeningsfractie (? = A s / A c) ?7,54 × 10 -2 (r0 = 0,75 %) elasticiteitsratio staal/beton (? e = E s/Ec) (zonder/met rel.) ? e 5,87 / 14,84 overdrachtslengte (l t = ? / 8? ; resp. ? / 6,4? ) l t 332 / 415 mm Tabel 1?Uitgangspunten berekening omschrijving symbool grootte sterkteklasse beton C35/45 (f ck,cube = 45 MPa) hydratatiesnelheid cement klasse N dikte beton h250 mm lengte L 0 25 m & 100 m gemiddelde relatieve vochtigheid RV50% ouderdom beton bij belasten t 0 28 dagen secant elasticiteitsmodulus beton E cm 34077 N/mm² elasticiteitsmodulus betonstaal E s 200.000 N/mm² diameter betonstaal (horizontale wapening) ?20 mm staafafstand (per zijde beton) b s 168 mm 50? CEMENT 5 20 21 Figuur 6b Optredende krachten tijden\f de krimp. Met re\baxatie. L 0 = 25 m, N c\f,max = 495,8 kN, bij c = 3,76 10 -6 m/m i\f N cr = 379,6 kN F iguur 7a Optredende krachten tijden\f de krimp. Zonder re\baxatie. L 0 = 100 m, N c\f,max = 495,8 kN, bij c = 3,67 10 -6 m/m i\f N cr = 422,6 kN 370 3 90 410 430 450 470 490 510 0,0E+00 5,0E-05 1,0E-04 1,5E-04 2,0E-04 2,5E-04 3,0E-04 3,5E-04 4,0E-04 kracht [kN ] rek [m/m] krimp L= 25 m met relaxatie 410 4 20 430 440 450 460 470 480 490 500 510 0,0E+00 5,0E-05 1,0E-04 1,5E-04 2,0E-04 2,5E-04 3,0E-04 3,5E-04 4,0E-04 kracht [kN ] rek [m/m] krimp L= 100 m zonder relaxatie Figuur 6b Optredende krachten tijden\f de krimp. Met re\baxatie. L 0 = 25 m, N c\f,max = 495,8 kN, bij c = 3,76 10 -6 m/m i\f N cr = 379,6 kN F iguur 7a Optredende krachten tijden\f de krimp. Zonder re\baxatie. L 0 = 100 m, N c\f,max = 495,8 kN, bij c = 3,67 10 -6 m/m i\f N cr = 422,6 kN 370 3 90 410 430 450 470 490 510 0,0E+00 5,0E-05 1,0E-04 1,5E-04 2,0E-04 2,5E-04 3,0E-04 3,5E-04 4,0E-04 kracht [kN ] rek [m/m] krimp L= 25 m met relaxatie 410 4 20 430 440 450 460 470 480 490 500 510 0,0E+00 5,0E-05 1,0E-04 1,5E-04 2,0E-04 2,5E-04 3,0E-04 3,5E-04 4,0E-04 kracht [kN ] rek [m/m] krimp L= 100 m zonder relaxatie Figuur 5 Geschematiseerde verdeling van de \feton- en staalspanningen in de ongescheurde \bones ( c1 en s1) en de staalspanning in de scheuren ( s2) F iguur 6a Optredende krachten tijdens de krimp. Zonder relaxatie. L 0 = 25 m, N cs,max = 495,8 kN, \fij c = 3,40 10 -6 m/m is N cr = 359,6 kN 340 3 60 380 400 420 440 460 480 500 0,0E+00 5,0E-05 1,0E-04 1,5E-04 2,0E-04 2,5E-04 3,0E-04 3,5E-04 4,0E-04 kracht [kN ] rek [m/m] krimp L= 25 m zonder relaxatie s/2 s1 s2 s2 s2 sl? s s lt l
? c1 + + + + + + - - - - L? N N + + + - s2 s lt Figuur 7b Optredende krachten tijden\f de krimp. Met re\baxatie. L 0 = 100 m, N c\f,max = 495,8 kN, bij c = 3,54 10 -6 m/m i\f N cr = 437,7 kN F iguur 8a Optredende krachten tijden\f de 20 ºC afkoe\bing. Zonder re\baxatie. L 0 = 25 m, N T,max = 517,7 kN, na ont\ftaan eer\fte \fcheur: N cr = 398,2 kN 430 4 40 450 460 470 480 490 500 510 0,0E+00 5,0E-05 1,0E-04 1,5E-04 2,0E-04 2,5E-04 3,0E-04 3,5E-04 4,0E-04 kracht [kN ] rek [m/m] krimp L= 100 m met relaxatie 390 4 10 430 450 470 490 510 530 0,0E+00 2,5E-05 5,0E-05 7,5E-05 1,0E-04 1,3E-04 1,5E-04 1,8E-04 2,0E-04 kracht [kN] rek [m/m] temperatuur L= 25 m zonder relaxatie Tabel 3?Resultaten krimpberekeningen relaxatie relaxatiecoëfficiënt ?lengte L 0 [m]afstand tussen scheuren [m] staalspanning ? s,cr [N/mm²] scheurwijdte [mm] zonder 1251,75265,10,27 met 0,4252,71265,10,25 zonder 11003,84265,10,27 met 0,41006,25265,10,25 4b 5b 4a 5a voor de berekeningen zijn samengevat in de tabellen 1 en 2. Voor de spanning bij scheuren van het beton ( ?cr) is uitgegaan van 60% van de gemiddelde 28-daagse (axiale) korteduur treksterkte van beton f ctm,0 [5]: ?cr = 0,6 f ctm,0 (10) met de g emiddelde korteduur treksterkte [6]: f ctm,0 = 0,9 [1,05 + 0,05(f ck,cube + 8)] ( 11)waarin: f ctm,0 = g emiddelde 28-daagse korteduur tr eksterkte van beton [N/mm²] f ck,cube = karakteristieke kubusdruksterkte v an beton [N/mm²] Om de invloed van relaxatie op de scheur- vorming te onderzoeken zijn berekeningen g emaakt zonder en met relaxatie. In de situ - atie zonder relaxatie is voor de berekening v an de overdrachtslengte ter plaatse van de scheur uitgegaan van een aanhechtspanning die tweemaal zo groot is als de gemiddelde betontreksterkte [7], waaruit volgt l t = Ø / 8 ?. 4a Optredende krachten tijdens de krimp. Zonder relaxatie. L 0 = 25 m, N cs,max = 495,8 kN, bij ? cs = 3,40 × 10 -6 m/m is N cr = 359,6 kN 4b Optredende krachten tijdens de krimp. Met relaxatie. L 0 = 25 m, N cs,max = 495,8 kN, bij ? cs = 3,76 × 10 -6 m/m is N cr = 379,6 kN 5a Optredende krachten tijdens de krimp. Zonder relaxatie. L 0 = 100 m, N cs,max = 495,8 kN, bij ? cs = 3,67 × 10 -6 m/m is N cr = 422,6 kN 5b Optredende krachten tijdens de krimp. Met relaxatie. L 0 = 100 m, N cs,max = 495,8 kN, bij ? cs = 3,54 × 10 -6 m/m is N cr = 437,7 kN CEMENT 5 2021 ?51 Figuur 7b Optredende krachten tijden\f de krimp. Met re\baxatie. L 0 = 100 m, N c\f,max = 495,8 kN, bij c = 3,54 10 -6 m/m i\f N cr = 437,7 kN F iguur 8a Optredende krachten tijden\f de 20 ºC afkoe\bing. Zonder re\baxatie. L 0 = 25 m, N T,max = 517,7 kN, na ont\ftaan eer\fte \fcheur: N cr = 398,2 kN 430 4 40 450 460 470 480 490 500 510 0,0E+00 5,0E-05 1,0E-04 1,5E-04 2,0E-04 2,5E-04 3,0E-04 3,5E-04 4,0E-04 kracht [kN ] rek [m/m] krimp L= 100 m met relaxatie 390 4 10 430 450 470 490 510 530 0,0E+00 2,5E-05 5,0E-05 7,5E-05 1,0E-04 1,3E-04 1,5E-04 1,8E-04 2,0E-04 kracht [kN] rek [m/m] temperatuur L = 25 m zonder relaxatie Figuur 8b Optredende krachten tijden\f de 20 º\b afkoeling. Met relaxatie. L 0 = 25 m, N T,max = 551,2 kN, na ont\ftaan eer\fte \fcheur: N cr = 480,0 kN F iguur 9a Optredende krachten tijden\f de 20 º\b afkoeling. Zonder relaxatie. L 0 = 100 m, N T,max = 517,7 kN, na ont\ftaan eer\fte \fcheur: N cr = 481,6 kN 470 4 80 490 500 510 520 530 540 550 560 0,0E+00 2,5E-05 5,0E-05 7,5E-05 1,0E-04 1,3E-04 1,5E-04 1,8E-04 2,0E-04 kracht [kN] rek [m/m] temperatuur L = 25 m met relaxatie 480 4 90 500 510 520 0,0E+00 2,5E-05 5,0E-05 7,5E-05 1,0E-04 1,3E-04 1,5E-04 1,8E-04 2,0E-04 kracht [kN] rek [m/m] temperatuur L = 100 m zonder relaxatie Figuur 8b Optredende krachten tijden\f de 20 º\b afkoeling. Met relaxatie. L 0 = 25 m, N T,max = 551,2 kN, na ont\ftaan eer\fte \fcheur: N cr = 480,0 kN F iguur 9a Optredende krachten tijden\f de 20 º\b afkoeling. Zonder relaxatie. L 0 = 100 m, N T,max = 517,7 kN, na ont\ftaan eer\fte \fcheur: N cr = 481,6 kN 470 4 80 490 500 510 520 530 540 550 560 0,0E+00 2,5E-05 5,0E-05 7,5E-05 1,0E-04 1,3E-04 1,5E-04 1,8E-04 2,0E-04 kracht [kN] rek [m/m] temperatuur L= 25 m met relaxatie 480 4 90 500 510 520 0,0E+00 2,5E-05 5,0E-05 7,5E-05 1,0E-04 1,3E-04 1,5E-04 1,8E-04 2,0E-04 kracht [kN] rek [m/m] temperatuur L = 100 m zonder relaxatie Figuur 9b Optredende krachten tijden\f de 20 º\b afkoeling. Met relaxatie. L 0 = 100 m, N T,max = 551,2 kN, na ont\ftaan eer\fte \fcheur: N cr = 531,5 kN 530 5 35 540 545 550 555 0,0E+00 2,5E-05 5,0E-05 7,5E-05 1,0E-04 1,3E-04 1,5E-04 1,8E-04 2,0E-04 kracht [kN] rek [m/m] temperatuur L= 100 m met relaxatie 6a Optredende krachten tijdens de 20 ºC afkoeling. Zonder relaxatie. L 0 = 25 m, N T,max = 517,7 kN, na ontstaan eerste scheur: N cr = 398,2 kN 6b Optredende krachten tijdens de 20 ºC afkoeling. Met relaxatie. L 0 = 25 m, N T,max = 551,2 kN, na ontstaan eerste scheur: N cr = 480,0 kN 7a  Optredende krachten tijdens de 20 ºC afkoeling. Zonder relaxatie. L 0 = 100 m, N T,max = 517,7 kN, na ontstaan eerste scheur: N cr = 481,6 kN 7b Optredende krachten tijdens de 20 ºC afkoeling. Met relaxatie. L 00 = 100 m, N T,max = 551,2 kN, na ontstaan eerste scheur: N cr = 531,5 kN Tabel 4?Resultaten temperatuurberekening relaxatie relaxatiecoëfficiënt ?lengte L 0[m]afstand tussen scheuren [m] staalspanning scheurwijdte [mm] zonder 1252,45276,80,29 met 0,4257,9 2294,80,31 zonder 11002,7276,80,29 met 0,41009,59294,80,31 In geval van een langdurig aanwezige constante belasting en/ of een wisselende be- lasting neemt de aanhechtspanning met cir- ca 25% af [8], dus tot circa 1,6 maal de gemid- delde betontreksterkte. In dit geval is voor de o verdrachtslengte uitgegaan van l t = Ø / 6,4 ?. In tabel 2 zijn de grootheden en para- meters weergegeven die onder andere zijn bepaald conform NEN-EN 1-1 [9]. Rekenvoorbeeld: resultaten krimpberekeningen In de figuren 4 en 5 is de trekkracht uitgezet als functie van de spanninggevende rek ( ?c?) in de betonverhardingen met een lengte van 25 m resp. 100 m. Relaxatie veroorzaakt een reductie van de stijfheid van het beton (zie vgl. 8) ten opzichte van de situatie zonder re- laxatie. Het gevolg hiervan is dat in geval van relaxatie de eerste scheur bij een grotere rek ontstaat en dat dan het totaal aantal scheuren kleiner is (fig. 4b en 5b). De staalspanning in de scheuren vari - eert bij de voortgaande scheurvorming tus- sen de maximale waarde ( ?s,cr = N cs,max / A s) en een kleinere waarde na het ontstaan van een volgende scheur. Of de terugval van de maximale trekkracht in werkelijkheid ook optreedt in betonverharding in doogaand- gewapend beton, over de hele lengte 'elastisch 6a 7a 6b 7b KRACHTEN EN VERVORMINGEN IN BETONVERHARDINGEN In het artikel 'Krachten en vervor- mingen in betonverhardingen' uit Cement 2021/2 [11], ook geschreven door Gustaaf Bouquet, wordt aan de hand van een voorbeeld beschreven hoe optredende ver - v ormingen en normaalkrachten, als gevolg van afkoeling, kunnen worden berekend, rekening houdend met grondwrijving en relaxatie. 52? CEMENT 5 20 21 ondersteund' op een laag asfalt, is onzeker. Daarom is voor de berekening van de scheur- wijdte de maximale waarde van de trekkracht aangehouden voor berekening van de staal- spanning in de scheuren. De scheurwijdte is in situaties met relaxatie iets kleiner in verge- lijking tot de waarde zonder relaxatie (tabel 3). Dit wordt veroorzaakt doordat in de scheur- wijdtevergelijking (vgl. 7) de stijfheidsfactor ?e groter is bij relaxatie (tabel 2). Rekenvoorbeeld: resultaten temperatuurberekeningen In de figuren 6 en 7 zijn de optredende trek- krachten in de betonverharding met een elementlengte van 25 en 100 m weergegeven. Ook bij een verlaging van de temperatuur ontstaat een abrupte terugval in de trek- kracht na het ontstaan van elke nieuwe scheur. Nu ontstaat bij de eerste scheur een grote terugval die bij voortgaande scheur- vorming steeds kleiner wordt. Relaxatie heeft ook bij trekkachten bij temperatuur- verlaging een dempend effect. Scheurvor- ming treedt later op en het aantal scheuren is ook minder. Met dezelfde motivatie als bij krimp is ook nu de staalspanning berekend op basis van de maximale trekkracht ( ?s,cr = N T,max / A s). Doordat bij een opgelegde vervorming door temperatuur ook het betonstaal wordt gerekt, ontstaat er een toename van de staalspanning in de scheur in geval relaxatie als gevolg van de grotere stijfheidsparameter ?e, en dus ook een iets grotere scheurwijdte (tabel 4). Scheurwijdte ? staalspanning in scheuren (temperatuur en krimp) Na het ontstaan van de eerste scheur bereikt de trekkracht in het betonstaal in de scheu- ren steeds de maximale waarde (bij krimp N cs,max ; bij afkoeling N T,max ). Het is onzeker in hoeverre de staalspanning in werkelijkheid afneemt door scheurvorming. Daarom wordt voorgesteld om de maximale waarden van de trekkracht aan te houden voor de berekening van staalspanning in de scheur: voor krimp: () () , ck,cube 5 s 0 ,8 mo s cr s,cr e cr Ø0 , 4 2 8 w E f ? ??? = ? ??? ? ? +? ???? ? 1 1 0, 8 = + cr s,cr = ()cr s,cr e1 =+ (12) v oor temperatuurdaling : () () , ck,cube 5 s 0 ,8 mo s cr s,cr e cr Ø0 , 4 2 8 w E f ? ??? = ? ??? ? ? +? ???? ? 1 1 0, 8 = + cr s,cr = ()cr s,cr e1 =+ (13) M et deze relaties voor de staalspanning in de scheuren kan de scheurwijdte worden berekend met de vergelijkingen 6 en 7. Met deze benadering heeft de grootte van de krimp of rek door temperatuurverla- ging geen invloed op de scheurwijdte. Het effect van relaxatie op de grootte van de scheurwijdte is nihil (tabel 3 en 4). Afstand tussen de scheuren Als gevolg van de relaxatie wordt de beton- verharding minder stijf. Dit heeft tot gevolg dat een grotere opgelegde vervorming nodig is om de eerste scheur te creëren en dat het aantal scheuren wordt beperkt. Dit heeft een grote invloed op de gemiddelde afstand tus- sen de scheuren (tabel 3 en 4). In de praktijk blijkt dat de afstand tussen de scheuren vaak onregelmatig is en er soms clustering van scheuren optreedt. Clustering van scheuren (Klaffende Risse) heeft een grotere scheur- wijdte tot gevolg en een nadelige invloed op de 'performance' van de weg en wil men daarom zo veel mogelijke beperken. Er zijn mogelijkheden om de onderlinge afstand t ussen de (dwars)scheuren in een betonver- harding meer gelijkmatig te laten optreden (zie [10]). Evaluatie Bij het bereiken van de scheurrek ontstaat de eerste scheur in het beton en neemt de trekkracht af. In geval van krimp wordt de afname van de trekkracht (van N cs,max naar N cr,n) steeds groter naarmate er meer scheu- ren ontstaan (fig. 4 en 5). Dit wordt veroor- zaakt doordat de bijdrage van het beton aan de stijfheid steeds kleiner wordt bij toename van het aantal scheuren. Bij scheurvorming als gevolg van een temperatuurdaling neemt de trekkracht ook direct af bij het ontstaan van elke nieuwe scheur. De absolute grootte van de terugval neemt in dit geval af (fig. 6 en 7) omdat een nieuwe scheur naar verhouding minder in- vloed heeft naarmate er voorgaand meer scheuren zijn gevormd. LITERATUUR 1?Falkner, H. (1969), Zur Frage der Rissbildung durch Eigen- und Zwäng- spannungen infolge Temperatur in Stahlbetonbauten, DAfStb Heft 208, p. 99. 2?Gilbert, R.I. (1992), Shrinkage Cracking in Fully Restrained Concrete Members, ACI Structural Journal, Vol. 89, No. 2, p. 141-149. 3?Breugel, K. van, Braam, C.R., Veen, C. van der, Walraven, J.C. (1996), Beton- constructies onder Temperatuur- en Krimpvervormingen ? Theorie en Praktijk, Betonpraktijkreeks 2, BetonPrisma, 's-Hertogenbosch, p. 225. 4?Trost, H. (1967), Auswirkungen des Superpositionsprinzips auf Kriech- und Relaxationsprobleme des Beton und Spanbeton, Beton- und Stahlbetonbau, Vol. 62, Heft 10, p. 230-238 & Heft 11, p. 261-269. 5?Al-Kubaisy, M.A., Young, A.G. (1975), Failure of concrete under sustained tension, Magazine of Concrete Research, Vol. 27, No. 92, p. 171-178. 6?Braam, C.R., Bouquet, G.Chr. (2003), De treksterkten van beton nader beschouwd, Cement 2003, nr. 7, p. 72-75. 7?Konig, G., Fehling, E. (1988), Zur Rissbreitenbeschrankung im Stahlbeton- bau, Beton- und Stahlbetonbau, Vol. 83, Heft 6, p. 161-167; Heft 7 p. 199-204. 8?CEB/FIP Model Code 1990, Chapters 7.4.3 / 7.4.4. 9?NEN-EN 1-1 +C2:2011/NB:2016, Eurocode 2: Ontwerp en berekening van betonconstructies ? Deel 1-1: Algemene regels voor gebouwen. 10?Ren, D., Houben, L., Rens, L., Beeldens, A.(2014), Active crack control for continuously reinforced concrete pavements in Belgium through partial surface notches, Publication at the 2014 Annual Meeting of the Transpor- tation Research Board (TRB 2014), p. 15. 11?Bouquet, G.Chr., Krachten en vervormingen in betonverhardingen, Cement 2021, nr. 2, p. 38-45. CEMENT 5 2021 ?53