Nu er in Nederland steeds hoger en slanker wordt gebouwd, blijken onze normen hierin niet te voorzien. Onderzoek naar wetenschappelijke publicaties en internationale regelgeving hebben een aantal praktische rekenregels opgeleverd waarmee ontwerpberekeningen kunnen worden uitgevoerd voor onder andere de toetsing van de invloed van winddynamica op comfort.
Berekeningsmethoden
dynamische responsies hoogbouw
Onderzoek naar praktische rekenregels
voor dynamische responsies door windbelasting
1 Impressie van de Baantoren in Rotterdam, de slankste woontoren van Europa,
bron: Powerhouse Company 28? CEMENT 6|7 2019
Nu er in Nederland steeds hoger en slanker
wordt gebouwd, blijken onze normen hierin niet te voorzien. Onderzoek naar
wetenschappelijke publicaties en
internationale regelgeving hebben een aantal praktische rekenregels opgeleverd waarmee ontwerpberekeningen kunnen worden
uitgevoerd voor onder andere de toetsing van de invloed van winddynamica op comfort.
tikelen en internationale rekenregels over
dynamische responsies.
Soorten dynamische responsies
Variaties van de windsnelheid in de lucht-
stroom waarin gebouwen zijn opgesteld,
hebben een fluctuerende (wind)belasting op
het gebouw tot gevolg, waardoor het gebouw
evenwijdig aan de wind een dynamische
respons geeft. Bovendien geeft de overstro-
ming (wind die langs het gebouw stroomt)
aanleiding tot het ontstaan van wervels en
daarmee ook een fluctuerende (wind)belas-
ting loodrecht op de eigenlijke windrichting
(het zogenoemde vortex-effect). Als laatste
kunnen alle fluctuerende (wind)belastingen
er ook voor zorgen dat het gebouw gaat
draaien om zijn (hoogte)as. We spreken dan
van een rotatieresponsie. In figuur 2 zijn de
drie afzonderlijke dynamische responsies
voor de Baantoren afgebeeld.
De dynamische responsie evenwijdig aan én
loodrecht op de windrichting veroorzaken
translatieversnellingen. De dynamische ro-
tatieresponsie veroorzaakt een rotatiever-
snelling rondom de verticale as van het ge-
IR. ROB TREELS RC
Projectleider /
Projectingenieur
IMd Raadgevende Ingenieurs auteur
1
In 2017 is IMd Raadgevende
Ingenieurs in samenwerking
met BREED Integraded Design
gestart met het constructief
ontwerp voor de Baantoren in
Rotterdam.
Deze woontoren van 150 m
hoog, met een breedte van 23 m en een
diepte van 20 m heeft een slankheid van 7,5
(verhouding hoogte/diepte). Het wordt daar-
mee de slankste woontoren van Europa (fig.
1). Uiteraard speelt winddynamica bij derge-
lijke hoge slanke torens een belangrijke rol.
Direct vanaf het begin was duidelijk dat
onze normen (NEN-EN 1991-1-4, Eurocode 1,
deel Windbelasting) hier helaas (nog) niet
volledig in voorzien. In het Convenant hoog -
bouw ? Deel 3: Constructieve veiligheid (NTA
4814-3) uit 2012 wordt in paragraaf 8.5.4 nog
beweerd dat het trillingsniveau bij resonan -
tie dwars op de windrichting lager zal zijn
dan bij resonantie evenwijdig aan de wind -
richting en dat deze dwarstrillingen daarom
niet afzonderlijk in rekening hoeven te wor-
den gebracht. Deze bewering kan bij hoge
slanke torens echter geen stand houden.
Voor de Baantoren is IMd daarom een on -
derzoek gestart naar wetenschappelijke ar-
CEMENT 6|7 2019 ?29
bouw. Uit deze rotatieversnelling zijn op
basis van de breedte en diepte van de ge-
bouwplattegrond ook de bijbehorende
translatieversnellingen te bepalen (fig. 3).
Verderop in dit artikel wordt nader ingegaan
op een combinatie van deze drie afzonderlij-
ke translatieversnellingen.
Toetsing van winddynamische
responsies
De dynamische responsie als gevolg van
windbelasting op gebouwen kan resulteren
in een (horizontale) vervorming van het ge-
bouw die groter is dan de vervorming ten
gevolge van statische windbelasting en zal
dus ook gepaard gaan met acceleraties. Voor
de toetsing van winddynamica wordt daar-
om onderscheid gemaakt tussen de toetsing
op vervorming/krachten en op versnelling.Voor de toetsing op vervorming (BGT)
en krachten (UGT) wordt in NEN-EN 1991-1-4
2?Overzicht van de drie mogelijke dynamische responsies
gebruikgemaakt van de zogenoemde bouw -
werkfactor c
scd, die wordt bepaald door de
afmetingsfactor c
s van het gebouw te verme-
nigvuldigen met de dynamische factor c
d
van het gebouw. De windbelasting op het ge-
bouw wordt vervolgens vermenigvuldigd
met deze bouwwerkfactor en hiermee wor-
den vervolgens alle gebruikelijke berekenin -
gen en toetsingen uitgevoerd.
Een winddynamische responsie veroorzaakt
naast horizontale vervormingen dus ook
versnellingen. En aangezien wij deze alleen
kunnen waarnemen met onze evenwichts-
organen, bepaalt de grootte van deze ver-
snellingen of wij ons hierbij wel of niet pret-
tig voelen. Er wordt daarom ook wel
gesproken van een comforttoets. In de nati -
onale bijlage van NEN-EN 1990 is een grafiek
gegeven (fig. 4) waarin grenswaarden voor
de (piek)versnelling in een verblijfsruimte
Voor de toetsing
van winddyna
mica wordt
onderscheid
gemaakt tussen
de toetsing op
vervorming/
krachten en op
versnelling
2
30? CEMENT 6|7 2019
zijn af te lezen, die afhankelijk zijn van de
eerste eigenfrequentie van het gebouw. In
deze grafiek wordt nog onderscheid ge-
maakt tussen gebouwen met een gebruiks-
klasse 1 (kantoor-, onderwijs- en industrie-
functie) en een gebruiksklasse 2
(bijeenkomst-, woon-, logies-, cel-, gezond-
heidszorg-, sport- en winkelfunctie). Deze
grenswaarde voor de (piek)versnelling mag
één maal per jaar optreden en zal uiteraard
optreden op de verblijfsruimten van de bo-
venste verdieping.
Belangrijkste parameters bij
dynamische windberekeningen
Naast de gebouwafmetingen (hoogte, breed -
te en diepte) volgens figuur 5 en de massa
(totale permanente belasting en het mo-
mentane deel van de veranderlijke vloerbe-
lastingen), zijn de parameters eigenfrequen -
tie, demping en windsnelheid van belang.
Deze parameters worden nu kort toegelicht.
Eigenfrequentie In NEN-EN 1991-1-4 wordt
een vereenvoudigde formule voor de eerste
eigenfrequentie gegeven:
(1)
Met de meeste FEM-programma's (3D) zijn
de eigenfrequenties ook te berekenen op ba -
sis van de ingevoerde modale massa's en de
(buig)stijfheid van de constructie. Met deze
twee uitgangspunten geeft de eerder in NEN
6702 opgenomen benaderingsformule voor
een 1D-staaf (die onderin oneindig stijf of
verend is ingeklemd) dezelfde nauwkeurige
waarde voor de eerste eigenfrequentie:
(2)
waarin ? de grootste (horizontale) uitbuiging
van de constructie voorstelt, indien de
1D-staaf horizontaal wordt belast met een
combinatie van de totale permanente belas-
ting en het momentane deel van de veran -
derlijke (vloer)belastingen.
Ook de trillingsvorm is van invloed op de dy -
namische responsie. Zo wordt in bijlage C
uit NEN-EN 1991-1-4 voor de comforttoets de
factor K gebruikt. De grootte hangt af van de
3?Relatie tussen translatie en rotatie(piek)versnellingen
4?Grafiek met grenswaarden voor versnellingen (figuur NB.2 uit nationale bijlage NENEN 1991 14)
5?Belangrijkste gebouwafmetingen
3
4
5
CEMENT 6|7 2019 ?31
eerste trillingsvorm, die uniform, lineair, pa-
rabolisch of sinusvormig over de hoogte kan
zijn. In bijlage B uit NEN-EN 1991-1-4 en an -
dere berekeningsmethoden wordt de eerste
trillingsvorm beschreven met de formule:
(3)
waarbij de exponentiële factor ? deze tril -
lingsvorm bepaalt (fig. 6).
Demping De dempingsmaat D van een
gebouw bepaalt de mate waarin de door
wind opgewekte dynamische kinetische
energie wordt omgezet naar hoofzakelijk
thermische energie (warmte). Door wrijving
in een constructiemateriaal tussen onder-
delen van een constructie of tussen
constructie en omgeving (bodem, lucht),
komt deze warmte vrij. Deze dempingsmaat D geeft de fractie
(of het percentage) aan ten opzichte van de
kritische demping (die nodig is om de con -
structie na een uitwijking direct terug te la -
ten keren in de evenwichtstoestand). In Eu -
rocode NEN-EN1991-1-4 wordt het
logaritmisch decrement van demping ? (ook
wel constructieve demping genoemd) ge-
hanteerd, zijnde: ? = 2?D. Demping is helaas (nog) niet vooraf
exact te berekenen en alleen achteraf door
metingen te bepalen. Voor de aan te houden demping bij ge-
bouwen wordt vaak onderscheid gemaakt
tussen gebouwen van gewapend beton en
staal, zo worden er bijvoorbeeld in het Itali -
aanse rapport CNR-DT 207/2008 twee aparte
formules gegeven [1]:
voor gebouwen van gewapend beton, h ? 30 m
voor gebouwen van staal, h ? 30 m
Ook zal de demping bij gebouwen van gewa -
pend beton in de UGT hoger zijn dan in de
BGT, omdat door het optreden van scheuren
er meer wrijvingswarmte zal ontstaan. In
NEN 6702 wordt in bijlage A.4 bij het bepalen
van de dynamische vergrotingsfactor ?
1
(UGT) voor gebouwen van gewapend beton
een dempingsmaat van 0,02 genoemd. In bij-
lage A.5 wordt bij het bepalen van de dyna -
mische vergrotingsfactor ?
2 (BGT) voor ge-
bouwen met een eigenfrequentie lager dan 1
Hz een dempingsmaat van 0,01 genoemd. In NEN-EN 1991-1-4 wordt voor gebou -
wen van gewapend beton een constructieve
demping ?
s van 0,10 (wat overeenkomt met
een dempingsmaat D van 0,016) gegeven en
voor stalen gebouwen wordt de helft aange-
houden. Hierbij mag dan volgens bijlage F.5
het logaritmisch decrement van de aerody -
namische demping ?
a ook nog worden op-
geteld.
In de Nederlandse vakliteratuur zijn de laat-
ste tijd diverse artikelen gewijd aan dem -
ping en dan met name in het kader van een
promotieonderzoek bij TNO. Er zijn vermoedens dat onze slappe
bodem en het gebruik van paalfunderingen
hierin een gunstig effect hebben en dus kun -
nen leiden tot hogere dempingswaarden bij
Nederlandse gebouwen. Dit wordt enigszins bevestigd door
6 Trillingsvormen
(4)
(5)
6
32? CEMENT 6|7 2019
metingen van TNO [2] aan vijftien Neder-
landse gebouwen (tien van gewapend beton
met een gemiddelde demping van 1,7% en
vijf van staal met een gemiddelde demping
van 2,2%).
Resumerend kan worden gesteld dat voor
toetsing op vervormingen (BGT) en versnel-
lingen (comfort) het aanhouden van een
dempingsmaat D van 1% aan de veilige kant is
en dat voor Nederlandse gebouwen wellicht
een hogere waarde van 1,5% realistisch is.
Windsnelheid Voor de in de dynamische
berekeningen te hanteren basiswindsnel -
heid worden internationaal nogal verschil -
lende definities gebruikt, zoals de snelheid
van een 3 s durende windstoot of de gemid -
delde windsnelheid over een periode van 10
min (o.a. NEN-EN 1991-1-4) of 1 uur (o.a. NEN
6702). Bij het vergelijken van de diverse
berekeningsmethoden moet daar dus reke-
ning mee worden gehouden. In NEN-EN 1991-1-4 is de grootte van
de basiswindsnelheid v
b;0 afhankelijk van het
windgebied (I, II of III) en de terreincatego-
rie (zee of kustgebied aan zee, onbebouwd
en bebouwd) en deze heeft dan een herha -
lingstijd (referentieperiode) van 50 jaar.
Voor windgebied II onbebouwd bedraagt de
basiswindsnelheid v
b;0 27,0 m/s en deze kan
vervolgens worden gebruikt bij een dynami -
sche toetsing op vervormingen (BGT) of
krachten (UGT). Voor een dynamische toet-
sing op versnellingen (comfort) geldt echter
een herhalingstijd van 1 jaar, zodat de basis-
windsnelheid mag worden gereduceerd met
een waarschijnlijkheidsfactor c
prob :
met
met R is herhalingstijd/refe-
rentieperiode in jaren
Met R = 1 jaar en K= 0,234 (bij windgebied II)
bedraagt de basiswindsnelheid v
b;0 19,5 m/s
die vervolgens kan worden gebruikt bij een
dynamische toetsing op comfort.
Met deze basiswindsnelheden kunnen ver-
volgens de gemiddelde windsnelheden op
een bepaalde hoogte z worden berekend. In de diverse berekeningsmethoden worden
ook nog verschillende hoogten aangehouden
op basis waarvan de gemiddelde windsnel
-
heid moet zijn bepaald. Zo wordt in NEN-EN
1991-1-4 deze gemiddelde windsnelheid be-
paald bij een referentiehoogte z
s (gelijk aan
0,6 h).
In de meeste berekeningsmethoden moet
voor de windbelasting ook een totale kracht-
coëfficiënt c
f als een combinatie van wind -
druk (bijvoorbeeld 0,8) en windzuiging (bij-
voorbeeld 0,5) worden ingevoerd. In de
nationale bijlage van NEN-EN 1991-1-4 is nog
gesteld dat vanwege het gebrek aan correla -
tie tussen die twee, deze krachtcoëfficiënt
met een factor van 0,85 mag worden geredu -
ceerd. Bij hoge slanke gebouwen is het raad -
zaam om met windtunnelonderzoek de
exacte windbelastingen en daarmee de
krachtcoëfficiënt c
f te bepalen.
Berekeningsmethoden
Bij het onderzoek zijn uiteindelijk vijf bere-
keningsmethoden gevonden om één of
meerdere van de eerdergenoemde drie dy -
namische responsies te kunnen berekenen.
Deze methoden worden kort toegelicht.
NEN 6702 In NEN 6702 kan alleen de dyna -
mische responsie evenwijdig aan de wind -
richting worden berekend. In bijlage A.4 kan
een vergrotingsfactor ?
1 worden bepaald,
die samen met de afmetingsfactor C
dim de
dynamische vergrotingsfactor voor de wind -
belasting bepaalt. In bijlage A.5 kan de
versnelling voor de regulier bepaalde eerste
eigenfrequentie en voor een verhoogde
eerste eigenfrequentie worden berekend.
Deze eenvoudige berekeningsmethode is
ook nog opgenomen in NEN-EN 1990.
NEN-EN 1991-1-4 De dynamische responsie
evenwijdig aan de windrichting is met Euro-
code NEN-EN 1991-1-4 volgens twee bereke-
ningsmethoden (bijlage B of C) te bepalen.
Door TNO is aangetoond dat de berekenings-
methode conform bijlage C nauwkeuriger
resultaten oplevert die beter aansluiten op
de theoretische modellen [3]. Met beide
berekeningsmethoden kan zowel de eerder-
genoemde bouwwerkfactor c
scd, als de maxi -
Bij het
onderzoek zijn
vijf berekenings
methoden
gevonden om
één of meerdere
van de drie
dynamische
responsies te
kunnen
berekenen
(6)
CEMENT 6|7 2019 ?33
male piek(translatie)versnelling op de
bovenste verdieping worden bepaald.In een artikel van TNO uit Bouwen met
Staal 204 uit 2008 [4] is aangegeven hoe met
bijlage C uit Eurocode NEN-EN 1991-1-4 on -
der andere ook een maximale piek(transla -
tie)versnelling op de bovenste verdieping
ten gevolge van de rotatieresponsie is te be-
palen. Voor de dynamische responsie lood -
recht op de windrichting wordt voor gebou -
wen geen berekeningsmethode gegeven. Om
toch een vergelijking met andere bereke-
ningsmethoden te kunnen maken, kan voor
deze dynamische responsie het gebouw in
dwarsrichting met windbelasting in dwars-
richting worden beschouwd.
Artikel Cement 1992/12 In het artikel 'Dyna -
mische belastingen (VI)' uit Cement 1992/12 [5], uit een langere reeks artikelen over
dynamische belastingen, wordt behandeld
hoe te rekenen aan beweging van gebouwen
als gevolg van wind. De theorie in dat artikel
is deels gebaseerd op het boek 'Windeffects
on Structures' [6].
Bij het reproduceren van het reken -
voorbeeld blijken twee formules in het arti -
kel helaas niet juist te zijn weergegeven, dus
voor de volledigheid worden hier de juiste
formules gegeven:
Bij deze methode wordt gerekend met de
uurgemiddelde windsnelheid op hoogte h
van het gebouw en deze wordt bepaald aan
(7)
(8)
7?Afdruk met in en uitvoer van de onlineberekeningsmethode DEDMHR
7
34? CEMENT 6|7 2019
de hand van de wrijvingssnelheid u * con-
form NEN 6702. Meer hierover is te lezen in
het TNO-rapport B-90-0483 [7]. Uiteindelijk zijn met deze berekenings-
methode de dynamische vervorming, de dy -
namische piek(translatie)versnelling even -
wijdig aan én loodrecht op de windrichting
en de dynamische piek(rotatie)versnelling te
bepalen.
Rapport CNR-DT 207/2008 In Italië is naar
aanleiding van het verschijnen van de Euro-
code het allesomvattende en zeer goed lees-
bare rapport CNR-DT 207/2008 uitgebracht,
waarin alle aspecten van windbelasting op
constructies met duidelijke voorbeelden
worden toegelicht [1]. Voor de dynamische responsie even -
wijdig aan de windrichting wordt de bereke-
ningsmethode volgens bijlage B uit Eurocode
NEN-EN 1991-1-4 gevolgd. Voor de dynamische responsie lood -
recht op de windrichting en voor de dynami -
sche rotatieresponsie worden de bereke-
ningsmethoden uit de Japanse norm AIJ
2004 gevolgd. Bij deze twee berekeningsme-
thoden moet voor het bepalen van de gemid -
delde windsnelheid de hoogte h worden aan -
gehouden, in tegenstelling tot de
berekeningsmethode volgens bijlage B uit
Eurocode NEN-EN 1991-1-4, waarin voor het
bepalen van de gemiddelde windsnelheid de
hoogte 0,6 h mag worden aangehouden.
Onlinerekentool DEDM-HR Door het NatHaz
Modelling Laboratory (University of Notre
Dame, USA) en het Wind Engineering Rese-
arch Center (Tamkang University, Taiwan) is
een onlinerekentool genaamd 'Databa -
se-Enabled Design Module ? High-Rise'
ontwikkeld (http://evovw.ce.nd.edu/dadm_
INT/VW_design6_INT1_noauth1.html),
waarmee dynamische berekeningen aan
gebouwen kunnen worden uitgevoerd. Er is
zelfs de mogelijkheid om met verschillende
internationale normen, waaronder ook de
Eurocode te rekenen [8, 9]. Met deze berekeningsmethode zijn on -
der andere de dynamische vervorming,
krachten, dynamische piek(translatie)ver-
snelling evenwijdig aan én loodrecht op de
windrichting en de dynamische piek(rotatie) versnelling te bepalen.
De meeste in te voeren variabelen zijn
in dit artikel ook al toegelicht, waarbij de
factor ß gelijk is aan de exponentiële factor
?, die de eerste trillingsvorm beschrijft. De
rotatieresponsie is onder andere afhankelijk
van de gemiddelde (rotatie)traagheidsstraal
Y, waar bij benadering de volgende formule
voor kan worden gebruikt:
Het soortelijk gewicht (?) van de lucht zelf is
mede bepalend voor de dynamische respon -
sies, in Nederland bedraagt deze waarde
1,25 kg/m
3.
In figuur 7 is een in- en uitvoer van
deze dynamische berekening weergegeven.
In de uitvoer is goed te zien dat er ook bij
deze rekenmethode onderscheid wordt ge-
maakt tussen de Survivability (krachten en
vervormingen) en de Serviceability (versnel -
lingen).
Combinatie van de drie
dynamische responsies
Nu met een aantal berekeningsmethoden de
drie verschillende dynamische responsies
kunnen worden berekend, is het nog de
vraag of en in hoeverre de drie bijbehorende
piek(translatie)versnellingen met elkaar
moeten worden gecombineerd. Aangezien de drie piek(translatie)ver-
snellingen a
//, a en a r (waarbij a r de vectori -
eel bij elkaar opgetelde piek(translatie)ver-
snellingen in de twee hoofdrichtingen uit de
dynamische rotatieresponsie zijn) samen
kunnen optreden, wordt in de literatuur [5,
6] ook wel de totale gecombineerde
piek(translatie)versnelling berekend door de
drie genoemde losse versnellingscomponen -
ten vectorieel bij elkaar op te tellen. Daarbij
kan door de niet-maatgevende componen -
ten met 30% te reduceren, rekening worden
gehouden met het feit dat het onwaarschijn -
lijk is dat alle drie de maxima tegelijkertijd
zullen optreden én het feit dat de eerste ei -
genfrequenties voor buiging meestal nooit
gelijk zullen zijn aan de eerste eigenfrequen -
tie voor torsie. Voorgaande combinatieregel kan dan
met de volgende formule worden samen gevat:
(9)
Er blijken
behoorlijke
verschillen te
zitten tussen
de uitkomsten
van de
dynamische
berekenings
methoden
CEMENT 6|7 2019 ?35
In het rapport CNR-DT 207/2008 worden
drie afzonderlijke lineaire combinatieregels
gegeven, waarbij verschillende weegfactoren
(waarvan sommige ook weer variabel zijn)
in rekening worden gebracht. Ook hier moet
de maatgevende combinatieregel worden
toegepast.Overigens zou het dan ook voor de
hand liggen om vanuit de dynamische wind -
berekeningen voor de toetsing op vervor-
ming (BGT) en krachten (UGT) dezelfde
maatgevende combinatieregel (en dan met
name van de responsie evenwijdig aan én
loodrecht op de windrichting) op te nemen.
Rekenvoorbeeld
Tot slot van dit artikel worden met een re-
kenvoorbeeld de uitkomsten van de ver-
schillende berekeningsmethoden met elkaar
vergeleken. Het rekenvoorbeeld betreft een
gebouw met een vierkante plattegrond
(b = d = 30 m) en een hoogte h van 210 m. In
figuur 7 bij de omschrijving van de online
berekeningsmethode DEDM-HR is ditzelfde
voorbeeld gebruikt. Het gebouw staat in Nederland in
windgebied II in een onbebouwde omgeving
en voor de krachtcoëfficiënt c
f wordt 1,5 aan -
gehouden. De massa van het gebouw be-
draagt 405.000 kg/m. De demping D bedraagt 0,01 en er
wordt geen aerodynamische demping in re-
kening gebracht. De eerste eigenfrequentie (in beide
hoofdrichtingen) voor buiging bedraagt 0,20
Hz en de eerste eigenfrequentie voor torsie
bedraagt 0,35 Hz. De verticale trillingsvorm
is lineair (? = 1,0). In figuur 8 zijn de resultaten van alle
vijf verschillende berekeningsmethoden
voor de zes piek(translatie)versnellingen
evenwijdig aan de wind in de comfortgra -
fiek geplot en in de naastgelegen tabel weer-
gegeven. In figuur 9 zijn de resultaten van de
vier verschillende berekeningsmethoden
voor de piek(translatie)versnellingen lood -
recht op de wind in de comfortgrafiek geplot
en in de naastgelegen tabel weergegeven. Hieruit blijkt dat de dynamische responsie
loodrecht op de windrichting bij twee van de
vier berekeningsmethoden groter is dan de
responsie evenwijdig aan de windrichting.
In figuur 10 zijn de resultaten van de
vier verschillende berekeningsmethoden
voor de vectorieel gesommeerde piek(trans-
latie)versnellingen ten gevolge van de
dynamische rotatieresponsie in de comfort-
grafiek geplot en in de naastgelegen tabel
weergegeven. In figuur 11 zijn de resultaten van de
vier verschillende berekeningsmethoden
voor de vier maatgevende combinaties van
alle piek(translatie)versnellingen in de com -
fortgrafiek geplot en in de naastgelegen
tabel weergegeven.
Uit diverse vergelijkingen van de bere-
keningsresultaten blijkt dat er behoorlijke
verschillen zitten tussen de gevonden dyna -
mische berekeningsmethoden. Elke bereke-
ningsmethode is dan ook gebaseerd op an -
dere theoretische modellen en heeft andere
uitgangspunten.
Tot slot
Met de beschikbare berekeningsmethoden
zijn op relatief eenvoudige wijze goede voor-
spellingen te doen over de dynamische
responsies van gebouwen op windbelasting.
Uiteraard kunnen dergelijke dynamische
responsies ook worden berekend met ge-
avanceerde 3D-FEM-computerprogram -
ma's, maar daarvoor moet dan wel een
dynamische windbelasting (bijvoorbeeld uit
een windtunneltest) bekend zijn. Er is behoefte aan verificatie van de
verschillende berekeningsmethoden door
veel meer metingen te verrichten aan gerea -
liseerde gebouwen, waarbij ook de demping
in de specifieke Nederlandse situatie nog
nader onderzocht moet worden. Vanuit TNO
worden hier dan ook nieuwe initiatieven
voor opgestart. In de nieuwe conceptversie
voor Eurocode NEN-EN 1991-1-4 zijn ook re-
kenregels voor de dynamische responsie
loodrecht op de windrichting én de dynami -
sche rotatieresponsie opgenomen.
LITERATUUR
1 Diverse uteurs, Technical Document CNR DT
207/2008 Guide for the assessment of wind acti
ons and effects on structures. National
Research Council Italy; June 2010.
2 Geurts, C.P.W., Bentum, C.A. van, Sanchez, S.,
Dijk, S. van, Demping hoogbouw voorspeld.
Cement 2015/3.
3 Steenbergen, R.D.J.M., Vrouwenvelder, A.C.W.M.,
Geurts, C.P.W., The use of Eurocode EN 1991 14
procedures
1 and 2 for building dynamics, a comparative
study. Journal of Wind
Engineering and Industrial Aerodynamics vol. 107 108;
August 2012.
4 Steenbergen, R.D.J.M., Geurts, C.P.W., Bentum,
C.A. van, Trillingen veroorzaakt door fluctuerende
windbelasting. Bouwen met Staal 204; oktober
2008.
5 Wisse, J.A., Staalduinen, P.C. van, Dynamische
Belastingen (VI) ?
Beweging van Gebouwen als gevolg van Wind.
Cement 1992/12.
6 Simiu, E., Scanlan, R.H., Windeffects on Structu
res, 3th Edition. John Wiley & Sons, 1996.
7 Staalduinen, P.C. van, Rapport
B90483 Achtergronden van de windbelastingen
volgens NEN 6702:1991. TNO Bouw Januari 1992
met correcties van September 1993.
8 Kwon, D., KijewskiCorrea, T., Kareem, A. e Ana
lysis of HighRise Buildings Subjected to Wind
Loads. Journal of Structural Engineering vol. 134; No.
7; July 2008 (ASCE).
9 Kwon, D., Kareem, A. A Multiple DatabaseEna
bled Design Module with Embedded Features of
International Codes and Standards. International
Journal of High-Rise Buildings vol. 2;
Nr. 3; September 2013.
(10)
36? CEMENT 6|7 2019
8 Berekeningsresultaten met (piek)versnellingen evenwijdig aan de windrichting
9 Berekeningsresultaten met (piek)versnellingen loodrecht op de windrichting
10 Berekeningsresultaten met vectorieel gesommeerde (piek)versnellingen t.g.v. de rotatieresponsie
11 Berekeningsresultaten met de maatgevende combinatie van de drie afzonderlijke (piek)versnellingen
8
9
10
11
CEMENT 6|7 2019 ?37
In 2017 is IMd Raadgevende Ingenieurs in samenwerking met BREED Integrated Design gestart met het constructief ontwerp voor de Baantoren in Rotterdam. Deze woontoren van 150 m hoog, met een breedte van 23 m en een diepte van 20 m heeft een slankheid van 7,5 (verhouding hoogte/diepte). Het wordt daarmee de slankste woontoren van Europa (fig. 1).

1. Impressie van de Baantoren in Rotterdam, de slankste woontoren van Europa (bron: Powerhouse Company)
Uiteraard speelt winddynamica bij dergelijke hoge slanke torens een belangrijke rol. Direct vanaf het begin was duidelijk dat onze normen (NEN-EN 1991-1-4, Eurocode 1, deel Windbelasting) hier helaas (nog) niet volledig in voorzien. In het Convenant hoogbouw - Deel 3: Constructieve veiligheid (NTA 4814-3) uit 2012 wordt in paragraaf 8.5.4 nog beweerd dat het trillingsniveau bij resonantie dwars op de windrichting lager zal zijn dan bij resonantie evenwijdig aan de windrichting en dat deze dwarstrillingen daarom niet afzonderlijk in rekening hoeven te worden gebracht. Deze bewering kan bij hoge slanke torens echter geen stand houden. Voor de Baantoren is IMd daarom een onderzoek gestart naar wetenschappelijke artikelen en internationale rekenregels over dynamische responsies.
Soorten dynamische responsies
Variaties van de windsnelheid in de luchtstroom waarin gebouwen zijn opgesteld, hebben een fluctuerende (wind)belasting op het gebouw tot gevolg, waardoor het gebouw evenwijdig aan de wind een dynamische respons geeft. Bovendien geeft de overstroming (wind die langs het gebouw stroomt) aanleiding tot het ontstaan van wervels en daarmee ook een fluctuerende (wind)belasting loodrecht op de eigenlijke windrichting (het zogenoemde vortex-effect). Als laatste kunnen alle fluctuerende (wind)belastingen er ook voor zorgen dat het gebouw gaat draaien om zijn (hoogte)as. We spreken dan van een rotatieresponsie. In figuur 2 zijn de drie afzonderlijke dynamische responsies voor de Baantoren afgebeeld.

2. Overzicht van de drie mogelijke dynamische responsies
De dynamische responsie evenwijdig aan én loodrecht op de windrichting veroorzaken translatieversnellingen. De dynamische rotatieresponsie veroorzaakt een rotatieversnelling rondom de verticale as van het gebouw. Uit deze rotatieversnelling zijn op basis van de breedte en diepte van de gebouwplattegrond ook de bijbehorende translatieversnellingen te bepalen (fig. 3). Verderop in dit artikel wordt nader ingegaan op een combinatie van deze drie afzonderlijke translatieversnellingen.
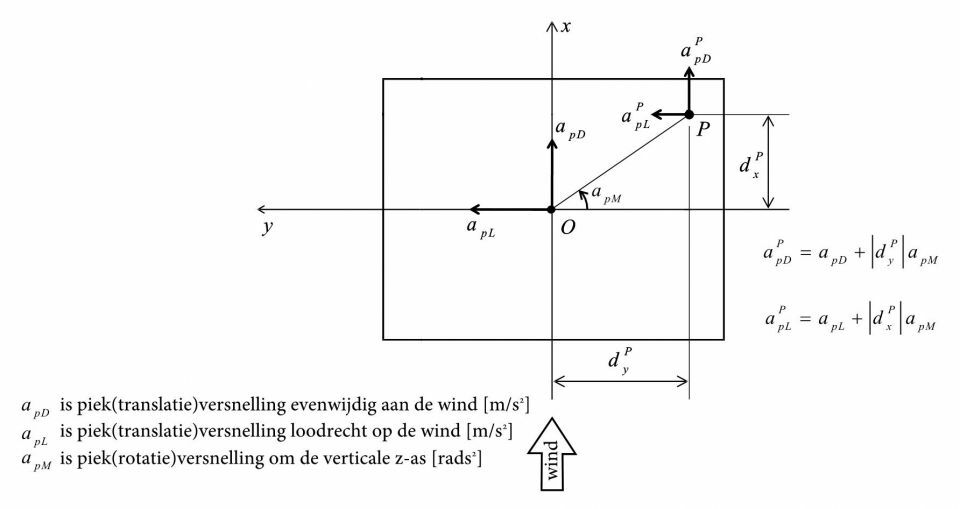
3. Relatie tussen translatie- en rotatie(piek)versnellingen
Voor de toetsing van winddynamica wordt onderscheid gemaakt tussen de toetsing op vervorming/krachten en op versnelling
Toetsing van winddynamische responsies
De dynamische responsie als gevolg van windbelasting op gebouwen kan resulteren in een (horizontale) vervorming van het gebouw die groter is dan de vervorming ten gevolge van statische windbelasting en zal dus ook gepaard gaan met acceleraties. Voor de toetsing van winddynamica wordt daarom onderscheid gemaakt tussen de toetsing op vervorming/krachten en op versnelling.
Voor de toetsing op vervorming (BGT) en krachten (UGT) wordt in NEN-EN 1991-1-4 gebruikgemaakt van de zogenoemde bouwwerkfactor cscd, die wordt bepaald door de afmetingsfactor cs van het gebouw te vermenigvuldigen met de dynamische factor cd van het gebouw. De windbelasting op het gebouw wordt vervolgens vermenigvuldigd met deze bouwwerkfactor en hiermee worden vervolgens alle gebruikelijke berekeningen en toetsingen uitgevoerd.
Een winddynamische responsie veroorzaakt naast horizontale vervormingen dus ook versnellingen. En aangezien wij deze alleen kunnen waarnemen met onze evenwichtsorganen, bepaalt de grootte van deze versnellingen of wij ons hierbij wel of niet prettig voelen. Er wordt daarom ook wel gesproken van een comforttoets. In de nationale bijlage van NEN-EN 1990 is een grafiek gegeven (fig. 4) waarin grenswaarden voor de (piek)versnelling in een verblijfsruimte zijn af te lezen, die afhankelijk zijn van de eerste eigenfrequentie van het gebouw. In deze grafiek wordt nog onderscheid gemaakt tussen gebouwen met een gebruiksklasse 1 (kantoor-, onderwijs- en industriefunctie) en een gebruiksklasse 2 (bijeenkomst-, woon-, logies-, cel-, gezondheidszorg-, sport- en winkelfunctie). Deze grenswaarde voor de (piek)versnelling mag één maal per jaar optreden en zal uiteraard optreden op de verblijfsruimten van de bovenste verdieping.
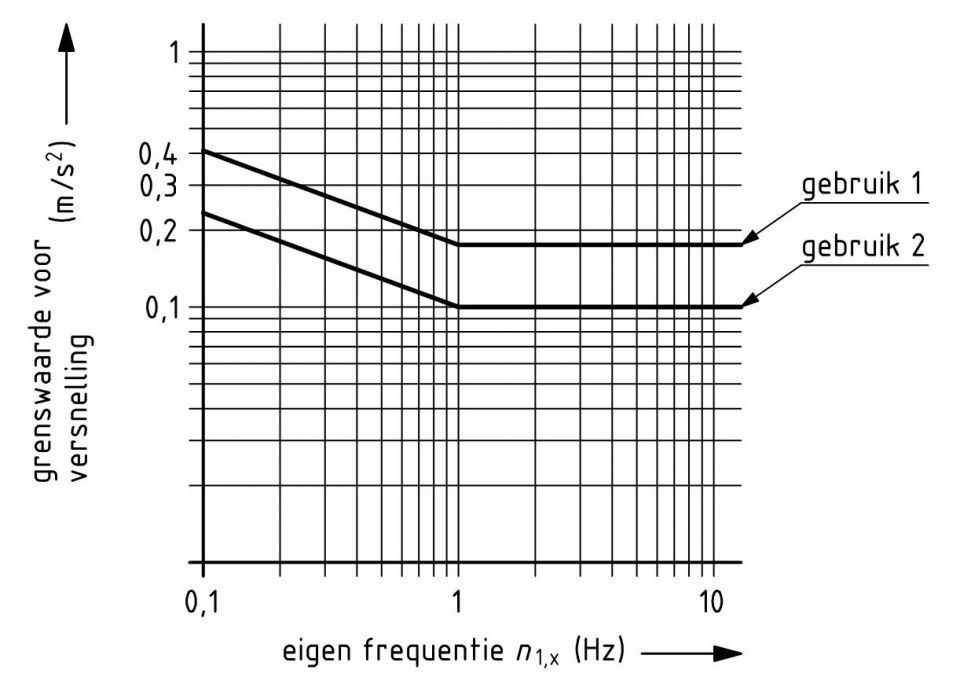
4. Grafiek met grenswaarden voor versnellingen (figuur NB.2 uit nationale bijlage NEN-EN 1991-1-4)
Voor dynamische windberekeningen zijn naast de gebouwafmetingen en de massa, ook de eigenfrequentie, demping en windsnelheid van belang
Belangrijkste parameters bij dynamische windberekeningen
Naast de gebouwafmetingen (hoogte, breedte en diepte) volgens figuur 5 en de massa (totale permanente belasting en het momentane deel van de veranderlijke vloerbelastingen), zijn de parameters eigenfrequentie, demping en windsnelheid van belang.
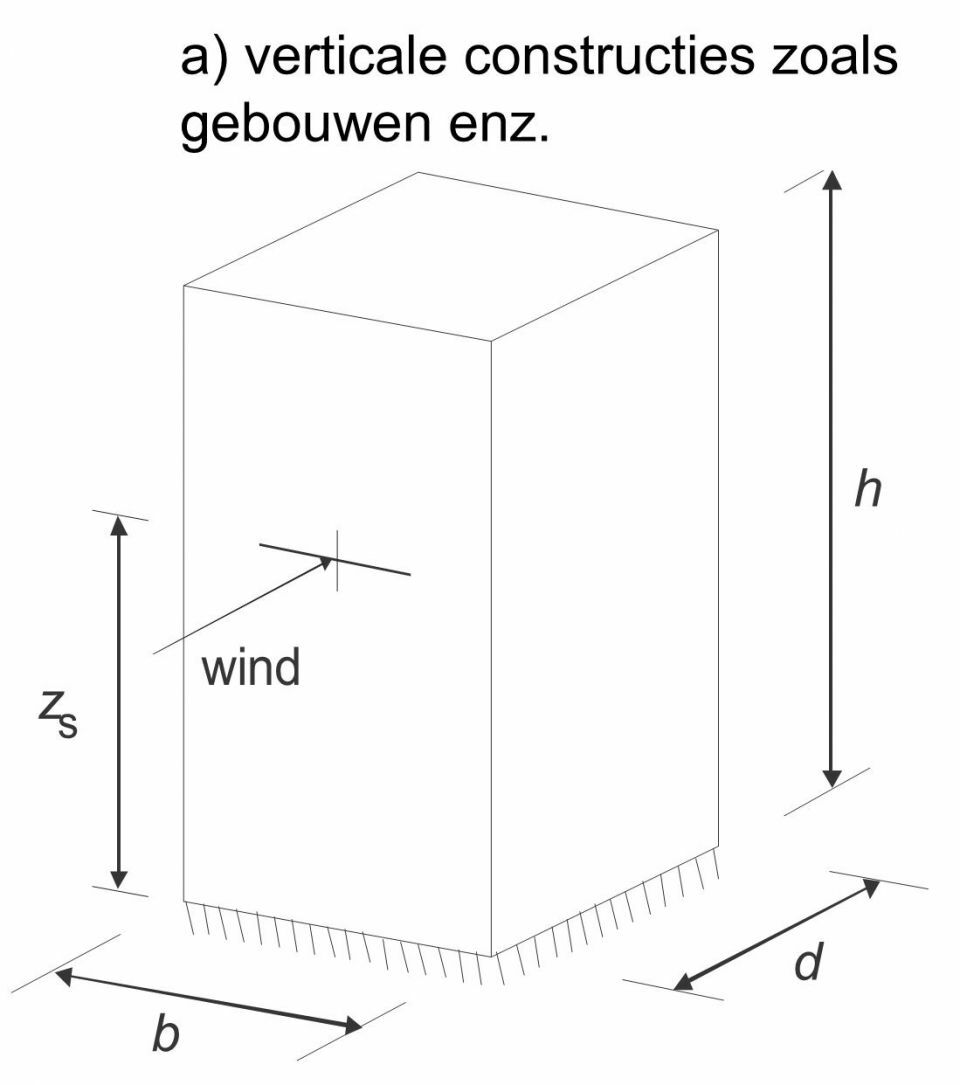
5. Belangrijkste gebouwafmetingen
Eigenfrequentie
In NEN-EN 1991-1-4 wordt een vereenvoudigde formule voor de eerste eigenfrequentie gegeven:
Met de meeste FEM-programma's (3D) zijn de eigenfrequenties ook te berekenen op basis van de ingevoerde modale massa's en de (buig)stijfheid van de constructie. Met deze twee uitgangspunten geeft de eerder in NEN 6702 opgenomen benaderingsformule voor een 1D-staaf (die onderin oneindig stijf of verend is ingeklemd) dezelfde nauwkeurige waarde voor de eerste eigenfrequentie:
waarin δ de grootste (horizontale) uitbuiging van de constructie voorstelt, indien de 1D-staaf horizontaal wordt belast met een combinatie van de totale permanente belasting en het momentane deel van de veranderlijke (vloer)belastingen.
Ook de trillingsvorm is van invloed op de dynamische responsie. Zo wordt in bijlage C uit NEN-EN 1991-1-4 voor de comforttoets de factor K gebruikt. De grootte hangt af van de eerste trillingsvorm, die uniform, lineair, parabolisch of sinusvormig over de hoogte kan zijn. In bijlage B uit NEN-EN 1991-1-4 en andere berekeningsmethoden wordt de eerste trillingsvorm beschreven met de formule:
waarbij de exponentiële factor ζ deze trillingsvorm bepaalt (fig. 6).
Demping
De dempingsmaat D van een gebouw bepaalt de mate waarin de door wind opgewekte dynamische kinetische energie wordt omgezet naar hoofzakelijk thermische energie (warmte). Door wrijving in een constructiemateriaal tussen onderdelen van een constructie of tussen constructie en omgeving (bodem, lucht), komt deze warmte vrij.
Deze dempingsmaat D geeft de fractie (of het percentage) aan ten opzichte van de kritische demping (die nodig is om de constructie na een uitwijking direct terug te laten keren in de evenwichtstoestand). In Eurocode NEN-EN1991-1-4 wordt het logaritmisch decrement van demping δ (ook wel constructieve demping genoemd) gehanteerd, zijnde: δ = 2πD.
Demping is helaas (nog) niet vooraf exact te berekenen en alleen achteraf door metingen te bepalen.
Voor de aan te houden demping bij gebouwen wordt vaak onderscheid gemaakt tussen gebouwen van gewapend beton en staal, zo worden er bijvoorbeeld in het Italiaanse rapport CNR-DT 207/2008 twee aparte formules gegeven [1]:
voor gebouwen van gewapend beton, h ≥ 30 m
voor gebouwen van staal, h ≥ 30 m
Ook zal de demping bij gebouwen van gewapend beton in de UGT hoger zijn dan in de BGT, omdat door het optreden van scheuren er meer wrijvingswarmte zal ontstaan. In NEN 6702 wordt in bijlage A.4 bij het bepalen van de dynamische vergrotingsfactor 1 (UGT) voor gebouwen van gewapend beton een dempingsmaat van 0,02 genoemd. In bijlage A.5 wordt bij het bepalen van de dynamische vergrotingsfactor 2 (BGT) voor gebouwen met een eigenfrequentie lager dan 1 Hz een dempingsmaat van 0,01 genoemd.
In NEN-EN 1991-1-4 wordt voor gebouwen van gewapend beton een constructieve demping s van 0,10 (wat overeenkomt met een dempingsmaat D van 0,016) gegeven en voor stalen gebouwen wordt de helft aangehouden. Hierbij mag dan volgens bijlage F.5 het logaritmisch decrement van de aerodynamische demping a ook nog worden opgeteld.
In de Nederlandse vakliteratuur zijn de laatste tijd diverse artikelen gewijd aan demping en dan met name in het kader van een promotieonderzoek bij TNO.
Er zijn vermoedens dat onze slappe bodem en het gebruik van paalfunderingen hierin een gunstig effect hebben en dus kunnen leiden tot hogere dempingswaarden bij Nederlandse gebouwen.
Dit wordt enigszins bevestigd door metingen van TNO [2] aan vijftien Nederlandse gebouwen (tien van gewapend beton met een gemiddelde demping van 1,7% en vijf van staal met een gemiddelde demping van 2,2%).
Resumerend kan worden gesteld dat voor toetsing op vervormingen (BGT) en versnellingen (comfort) het aanhouden van een dempingsmaat D van 1% aan de veilige kant is en dat voor Nederlandse gebouwen wellicht een hogere waarde van 1,5% realistisch is.
Windsnelheid
Voor de in de dynamische berekeningen te hanteren basiswindsnelheid worden internationaal nogal verschillende definities gebruikt, zoals de snelheid van een 3 s durende windstoot of de gemiddelde windsnelheid over een periode van 10 min (o.a. NEN-EN 1991-1-4) of 1 uur (o.a. NEN 6702). Bij het vergelijken van de diverse berekeningsmethoden moet daar dus rekening mee worden gehouden.
In NEN-EN 1991-1-4 is de grootte van de basiswindsnelheid vb;0 afhankelijk van het windgebied (I, II of III) en de terreincategorie (zee of kustgebied aan zee, onbebouwd en bebouwd) en deze heeft dan een herhalingstijd (referentieperiode) van 50 jaar. Voor windgebied II onbebouwd bedraagt de basiswindsnelheid vb;0 27,0 m/s en deze kan vervolgens worden gebruikt bij een dynamische toetsing op vervormingen (BGT) of krachten (UGT). Voor een dynamische toetsing op versnellingen (comfort) geldt echter een herhalingstijd van 1 jaar, zodat de basiswindsnelheid mag worden gereduceerd met een waarschijnlijkheidsfactor cprob:
met met R is herhalingstijd/referentieperiode in jaren
Met R = 1 jaar en K= 0,234 (bij windgebied II) bedraagt de basiswindsnelheid vb;0 19,5 m/s die vervolgens kan worden gebruikt bij een dynamische toetsing op comfort.
Met deze basiswindsnelheden kunnen vervolgens de gemiddelde windsnelheden op een bepaalde hoogte z worden berekend. In de diverse berekeningsmethoden worden ook nog verschillende hoogten aangehouden op basis waarvan de gemiddelde windsnelheid moet zijn bepaald. Zo wordt in NEN-EN 1991-1-4 deze gemiddelde windsnelheid bepaald bij een referentiehoogte zs (gelijk aan 0,6 h).
In de meeste berekeningsmethoden moet voor de windbelasting ook een totale krachtcoëfficiënt cf als een combinatie van winddruk (bijvoorbeeld 0,8) en windzuiging (bijvoorbeeld 0,5) worden ingevoerd. In de nationale bijlage van NEN-EN 1991-1-4 is nog gesteld dat vanwege het gebrek aan correlatie tussen die twee, deze krachtcoëfficiënt met een factor van 0,85 mag worden gereduceerd. Bij hoge slanke gebouwen is het raadzaam om met windtunnelonderzoek de exacte windbelastingen en daarmee de krachtcoëfficiënt cf te bepalen.
Bij het onderzoek zijn vijf berekeningsmethoden gevonden om één of meerdere van de drie dynamische responsies te kunnen berekenen
Berekeningsmethoden
Bij het onderzoek zijn uiteindelijk vijf berekeningsmethoden gevonden om één of meerdere van de eerdergenoemde drie dynamische responsies te kunnen berekenen. Deze methoden worden kort toegelicht.
NEN 6702
In NEN 6702 kan alleen de dynamische responsie evenwijdig aan de windrichting worden berekend. In bijlage A.4 kan een vergrotingsfactor 1 worden bepaald, die samen met de afmetingsfactor Cdim de dynamische vergrotingsfactor voor de windbelasting bepaalt. In bijlage A.5 kan de versnelling voor de regulier bepaalde eerste eigenfrequentie en voor een verhoogde eerste eigenfrequentie worden berekend. Deze eenvoudige berekeningsmethode is ook nog opgenomen in NEN-EN 1990.
NEN-EN 1991-1-4
De dynamische responsie evenwijdig aan de windrichting is met Eurocode NEN-EN 1991-1-4 volgens twee berekeningsmethoden (bijlage B of C) te bepalen. Door TNO is aangetoond dat de berekeningsmethode conform bijlage C nauwkeuriger resultaten oplevert die beter aansluiten op de theoretische modellen [3]. Met beide berekeningsmethoden kan zowel de eerdergenoemde bouwwerkfactor cscd, als de maximale piek(translatie)versnelling op de bovenste verdieping worden bepaald.
In een artikel van TNO uit Bouwen met Staal 204 uit 2008 [4] is aangegeven hoe met bijlage C uit Eurocode NEN-EN 1991-1-4 onder andere ook een maximale piek(translatie)versnelling op de bovenste verdieping ten gevolge van de rotatieresponsie is te bepalen.
Voor de dynamische responsie loodrecht op de windrichting wordt voor gebouwen geen berekeningsmethode gegeven. Om toch een vergelijking met andere berekeningsmethoden te kunnen maken, kan voor deze dynamische responsie het gebouw in dwarsrichting met windbelasting in dwarsrichting worden beschouwd.
Artikel Cement 1992/12
In het artikel 'Dynamische belastingen (VI)' uit Cement 1992/12 [5], uit een langere reeks artikelen over dynamische belastingen, wordt behandeld hoe te rekenen aan beweging van gebouwen als gevolg van wind. De theorie in dat artikel is deels gebaseerd op het boek 'Windeffects on Structures' [6].
Bij het reproduceren van het rekenvoorbeeld blijken twee formules in het artikel helaas niet juist te zijn weergegeven, dus voor de volledigheid worden hier de juiste formules gegeven:
(12)
(19)
Bij deze methode wordt gerekend met de uurgemiddelde windsnelheid op hoogte h van het gebouw en deze wordt bepaald aan de hand van de wrijvingssnelheid u* conform NEN 6702. Meer hierover is te lezen in het TNO-rapport B-90-0483 [7].
Uiteindelijk zijn met deze berekeningsmethode de dynamische vervorming, de dynamische piek(translatie)versnelling evenwijdig aan én loodrecht op de windrichting en de dynamische piek(rotatie)versnelling te bepalen.
Rapport CNR-DT 207/2008
In Italië is naar aanleiding van het verschijnen van de Eurocode het allesomvattende en zeer goed leesbare rapport CNR-DT 207/2008 uitgebracht, waarin alle aspecten van windbelasting op constructies met duidelijke voorbeelden worden toegelicht [1].
Voor de dynamische responsie evenwijdig aan de windrichting wordt de berekeningsmethode volgens bijlage B uit Eurocode NEN-EN 1991-1-4 gevolgd.
Voor de dynamische responsie loodrecht op de windrichting en voor de dynamische rotatieresponsie worden de berekeningsmethoden uit de Japanse norm AIJ 2004 gevolgd. Bij deze twee berekeningsmethoden moet voor het bepalen van de gemiddelde windsnelheid de hoogte h worden aangehouden, in tegenstelling tot de berekeningsmethode volgens bijlage B uit Eurocode NEN-EN 1991-1-4, waarin voor het bepalen van de gemiddelde windsnelheid de hoogte 0,6 h mag worden aangehouden.
Onlinerekentool DEDM-HR
Door het NatHaz Modelling Laboratory (University of Notre Dame, USA) en het Wind Engineering Research Center (Tamkang University, Taiwan) is een onlinerekentool genaamd 'Database-Enabled Design Module - High-Rise' ontwikkeld, waarmee dynamische berekeningen aan gebouwen kunnen worden uitgevoerd. Er is zelfs de mogelijkheid om met verschillende internationale normen, waaronder ook de Eurocode te rekenen [8, 9].
Met deze berekeningsmethode zijn onder andere de dynamische vervorming, krachten, dynamische piek(translatie)versnelling evenwijdig aan én loodrecht op de windrichting en de dynamische piek(rotatie)versnelling te bepalen.
De meeste in te voeren variabelen zijn in dit artikel ook al toegelicht, waarbij de factor β gelijk is aan de exponentiële factor ζ, die de eerste trillingsvorm beschrijft. De rotatieresponsie is onder andere afhankelijk van de gemiddelde (rotatie)traagheidsstraal Y, waar bij benadering de volgende formule voor kan worden gebruikt:
Het soortelijk gewicht (ρ) van de lucht zelf is mede bepalend voor de dynamische responsies, in Nederland bedraagt deze waarde 1,25 kg/m3.
In figuur 7 is een in- en uitvoer van deze dynamische berekening weergegeven. In de uitvoer is goed te zien dat er ook bij deze rekenmethode onderscheid wordt gemaakt tussen de Survivability (krachten en vervormingen) en de Serviceability (versnellingen).
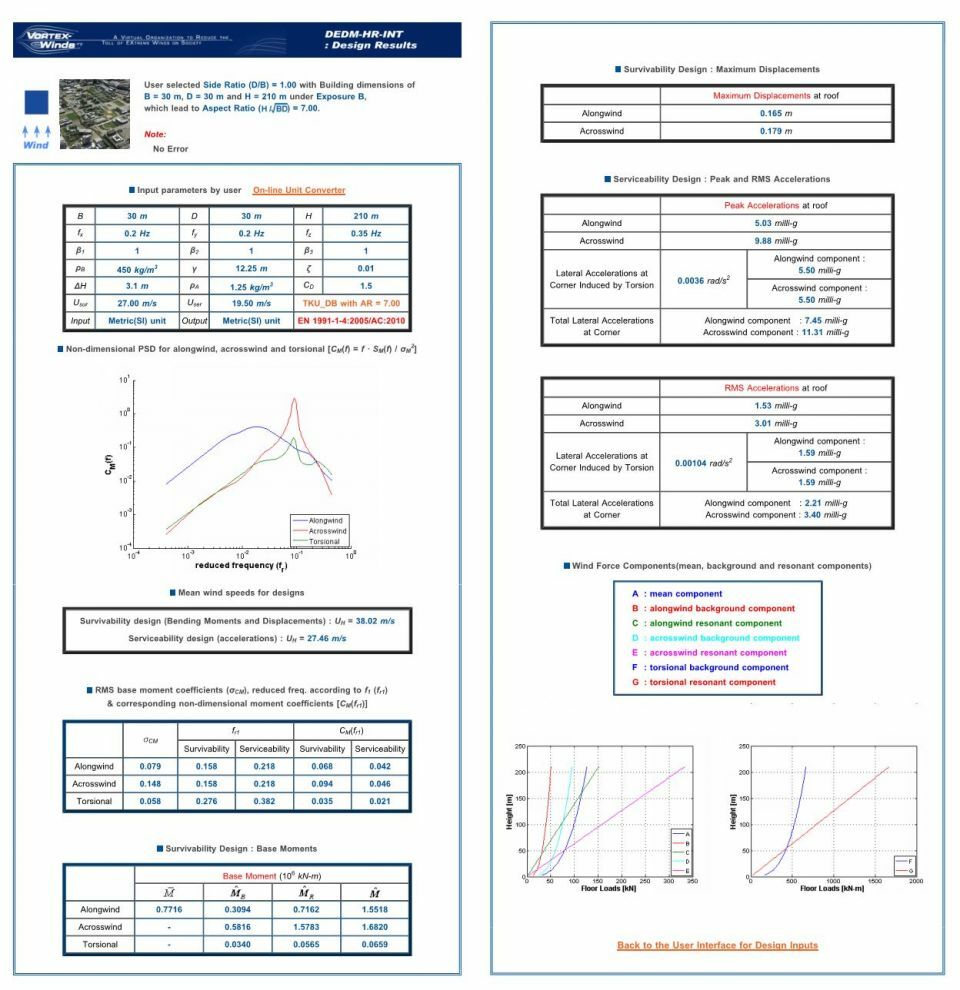
7. Afdruk met in- en uitvoer van de onlineberekeningsmethode DEDM-HR
Combinatie van de drie dynamische responsies
Nu met een aantal berekeningsmethoden de drie verschillende dynamische responsies kunnen worden berekend, is het nog de vraag of en in hoeverre de drie bijbehorende piek(translatie)versnellingen met elkaar moeten worden gecombineerd.
Aangezien de drie piek(translatie)versnellingen a//, en ar (waarbij ar de vectorieel bij elkaar opgetelde piek(translatie)versnellingen in de twee hoofdrichtingen uit de dynamische rotatieresponsie zijn) samen kunnen optreden, wordt in de literatuur [5, 6] ook wel de totale gecombineerde piek(translatie)versnelling berekend door de drie genoemde losse versnellingscomponenten vectorieel bij elkaar op te tellen. Daarbij kan door de niet-maatgevende componenten met 30% te reduceren, rekening worden gehouden met het feit dat het onwaarschijnlijk is dat alle drie de maxima tegelijkertijd zullen optreden én het feit dat de eerste eigenfrequenties voor buiging meestal nooit gelijk zullen zijn aan de eerste eigenfrequentie voor torsie.
Voorgaande combinatieregel kan dan met de volgende formule worden samengevat:
In het rapport CNR-DT 207/2008 worden drie afzonderlijke lineaire combinatieregels gegeven, waarbij verschillende weegfactoren (waarvan sommige ook weer variabel zijn) in rekening worden gebracht. Ook hier moet de maatgevende combinatieregel worden toegepast.
Overigens zou het dan ook voor de hand liggen om vanuit de dynamische windberekeningen voor de toetsing op vervorming (BGT) en krachten (UGT) dezelfde maatgevende combinatieregel (en dan met name van de responsie evenwijdig aan én loodrecht op de windrichting) op te nemen.
Rekenvoorbeeld
Tot slot van dit artikel worden met een rekenvoorbeeld de uitkomsten van de verschillende berekeningsmethoden met elkaar vergeleken. Het rekenvoorbeeld betreft een gebouw met een vierkante plattegrond (b = d = 30 m) en een hoogte h van 210 m. In figuur 7 bij de omschrijving van de onlineberekeningsmethode DEDM-HR is ditzelfde voorbeeld gebruikt.
Het gebouw staat in Nederland in windgebied II in een onbebouwde omgeving en voor de krachtcoëfficiënt cf wordt 1,5 aangehouden. De massa van het gebouw bedraagt 405.000 kg/m.
De demping D bedraagt 0,01 en er wordt geen aerodynamische demping in rekening gebracht.
De eerste eigenfrequentie (in beide hoofdrichtingen) voor buiging bedraagt 0,20 Hz en de eerste eigenfrequentie voor torsie bedraagt 0,35 Hz. De verticale trillingsvorm is lineair (ζ = 1,0).
In figuur 8 zijn de resultaten van alle vijf verschillende berekeningsmethoden voor de zes piek(translatie)versnellingen evenwijdig aan de wind in de comfortgrafiek geplot en in de naastgelegen tabel weergegeven.
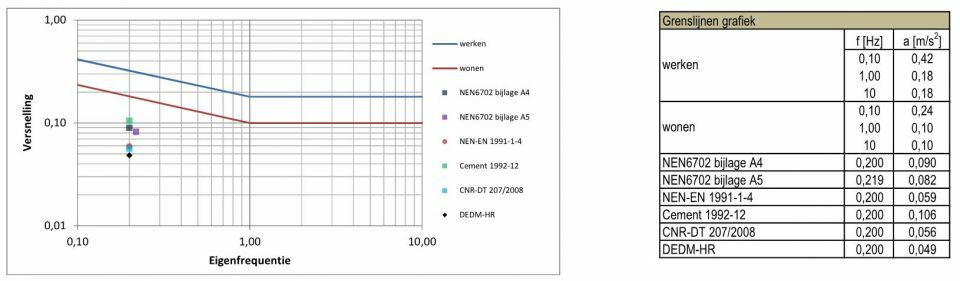
8. Berekeningsresultaten met (piek)versnellingen evenwijdig aan de windrichting
In figuur 9 zijn de resultaten van de vier verschillende berekeningsmethoden voor de piek(translatie)versnellingen loodrecht op de wind in de comfortgrafiek geplot en in de naastgelegen tabel weergegeven. Hieruit blijkt dat de dynamische responsie loodrecht op de windrichting bij twee van de vier berekeningsmethoden groter is dan de responsie evenwijdig aan de windrichting.
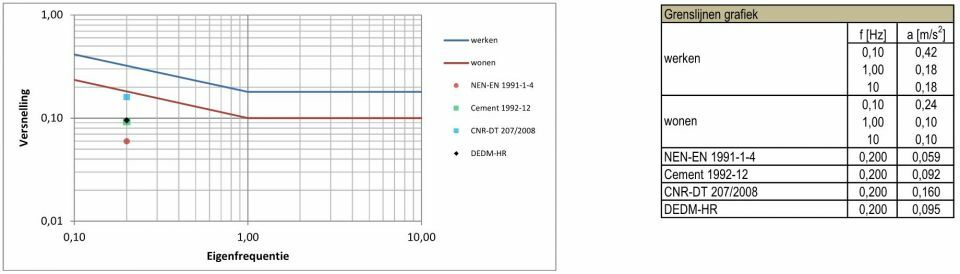
9. Berekeningsresultaten met (piek)versnellingen loodrecht op de windrichting
In figuur 10 zijn de resultaten van de vier verschillende berekeningsmethoden voor de vectorieel gesommeerde piek(translatie)versnellingen ten gevolge van de dynamische rotatieresponsie in de comfortgrafiek geplot en in de naastgelegen tabel weergegeven.
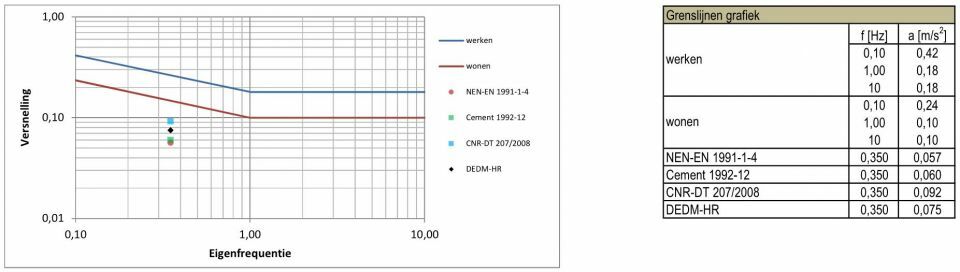
10. Berekeningsresultaten met vectorieel gesommeerde (piek)versnellingen t.g.v. de rotatieresponsie
In figuur 11 zijn de resultaten van de vier verschillende berekeningsmethoden voor de vier maatgevende combinaties van alle piek(translatie)versnellingen in de comfortgrafiek geplot en in de naastgelegen tabel weergegeven.
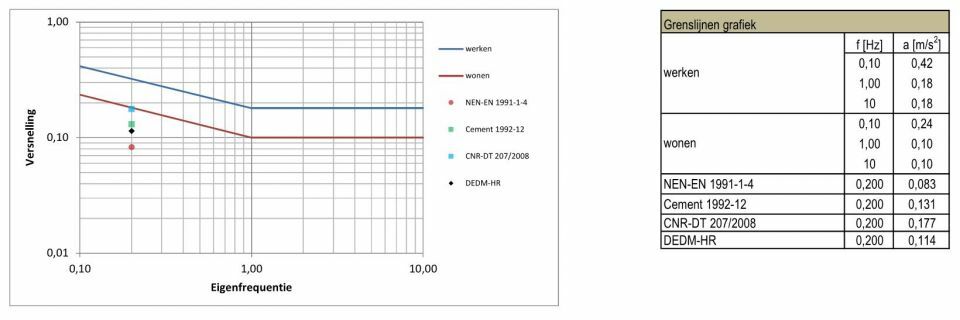
11. Berekeningsresultaten met de maatgevende combinatie van de drie afzonderlijke (piek)versnellingen
Er blijken behoorlijke verschillen te zitten tussen de uitkomsten van de dynamische berekeningsmethoden
Tot slot
Met de beschikbare berekeningsmethoden zijn op relatief eenvoudige wijze goede voorspellingen te doen over de dynamische responsies van gebouwen op windbelasting. Uiteraard kunnen dergelijke dynamische responsies ook worden berekend met geavanceerde 3D-FEM-computerprogramma's, maar daarvoor moet dan wel een dynamische windbelasting (bijvoorbeeld uit een windtunneltest) bekend zijn.
Er is behoefte aan verificatie van de verschillende berekeningsmethoden door veel meer metingen te verrichten aan gerealiseerde gebouwen, waarbij ook de demping in de specifieke Nederlandse situatie nog nader onderzocht moet worden. Vanuit TNO worden hier dan ook nieuwe initiatieven voor opgestart. In de nieuwe conceptversie voor Eurocode NEN-EN 1991-1-4 zijn ook rekenregels voor de dynamische responsie loodrecht op de windrichting én de dynamische rotatieresponsie opgenomen.
Literatuur
- Diverse auteurs, Technical Document CNR-DT 207/2008 Guide for the assessment of wind actions and effects on structures. National Research Council Italy; June 2010.
- Geurts, C.P.W., Bentum, C.A. van, Sanchez, S., Dijk, S. van, Demping hoogbouw voorspeld. Cement 2015/3.
- Steenbergen, R.D.J.M., Vrouwenvelder, A.C.W.M., Geurts, C.P.W., The use of Eurocode EN 1991-1-4 procedures 1 and 2 for building dynamics, a comparative study. Journal of Wind Engineering and Industrial Aerodynamics vol. 107-108; August 2012.
- Steenbergen, R.D.J.M., Geurts, C.P.W., Bentum, C.A. van, Trillingen veroorzaakt door fluctuerende windbelasting. Bouwen met Staal 204; oktober 2008.
- Wisse, J.A., Staalduinen, P.C. van, Dynamische Belastingen (VI) - Beweging van Gebouwen als gevolg van Wind. Cement 1992/12.
- Simiu, E., Scanlan, R.H., Windeffects on Structures, 3th Edition. John Wiley & Sons, 1996.
- Staalduinen, P.C. van, Rapport B-90-483 Achtergronden van de windbelastingen volgens NEN 6702:1991. TNO Bouw Januari 1992 met correcties van September 1993.
- Kwon, D., Kijewski-Correa, T., Kareem, A. e-Analysis of High-Rise Buildings Subjected to Wind Loads. Journal of Structural Engineering vol. 134; No. 7; July 2008 (ASCE).
- Kwon, D., Kareem, A. A Multiple Database-Enabled Design Module with Embedded Features of International Codes and Standards. International Journal of High-Rise Buildings vol. 2; Nr. 3; September 2013.


Reacties
Ingrid van Doorn - Imd 22 april 2020 20:40
Wat een fantastisch artikel!
Swinkels - De Paal 22 april 2020 18:32
Rob verdient deze erkenning dubbel en dwars