Realistic structural simulation is one of the new approaches for assessment of existing structures as well as for the design of new ones. This approach is supported now by the new fib model code 2010. In the current Eurocode it is supported in EN1992-2, and it will be one of the new features in the newly developed Eurocodes. ATENA software (2020) supports these new design and assessment concepts . In addition it is possible to couple them with durability models allowing the engineers to make predictions of the structural reliability also into the future. In this paper the developed models are demonstrated on applications to an existing bridge structure in Germany.
By Jan Cervenka and Libor Jendele (Cervenka Consulting s.r.o., Prague, Czech Republic), and Jiri Zalsky (Klokner’s Institute, Czech Technical University, Prague, Czech Republic)
- Gesponsord artikel -
The important aspect of realistic structural simulation is the new safety formats for structural assessment by numerical simulation, the so called ’digital twin approach’. The application of this new concept is presented on an example from structural health assessment of a concrete bridge combining advanced monitoring, structural simulation and durability models for chloride ingress and reinforcement corrosion.
The applied chemo-mechanical model covers initiation and propagation of chlorides or carbonation. This model is combined with the nonlinear modelling of cracking, bond failure and reinforcement yielding (Cervenka and Papanikolaou (2008)). The paper describes the previously developed model by the authors Hájková et al. (2019), Jendele, Šmilauer and Cervenka (2014). The models were implemented in ATENA software and are validated on experimental data. The developed models can be efficiently used in large scale analysis of real engineering problems as demonstrated on applications to an existing bridge structure in Germany (Cervenka et al. 2020). The example simulation using the digital twin concept shows time development of reinforcement corrosion due to chloride ingress, and the impact on the evolution of structural safety and reliability.
Authors are actively involved in the technical committees preparing the new Eurocodes for reinforced concrete design as well as the new fib model code 2020. The simulation by nonlinear analysis is being used by engineers for the design of reinforced concrete structures, but until recently no suitable safety formats were available. The first concise treatment of this problem has been developed in the international fib model 2010. An important aspect of the reinforced concrete design by simulation is also suitable estimation of model uncertainties, which are inherently strongly dependent on the software, the numerical approach and the user. A typical feature of the simulation-based design is the global safety format, which is different from a sectional local check in the standard design approach.
The sources of uncertainty in the reliability analysis are of two kinds, an aleatory uncertainty of material or geometric properties, which can be described by probabilistic models, and an epistemic uncertainty of models reflecting a lack of knowledge. The global design formats with different levels of probabilistic approximation are briefly discussed. In the presented example of bridge assessment the ECOV global resistance method is used (Cervenka V. 2008).
For application in predictions of structural reliability, it is necessary to take into account the possible degradation processes. In reinforced concrete structures, the reinforcement corrosion due to carbonation and chloride ingress are important damaging mechanisms. They can significantly reduce the service life of reinforced concrete structures (Tang, Utgenannt and Boubitsas 2015). Chloride ingress is usually the consequence of de-icing, sea water and salts in coastal areas. Ions from chloride penetrate through the concrete binder and their diffusion is governed by several factors such as environmental boundary conditions, concrete cover thickness, cement type, water-to-binder ratio (w/b) (Kwon et al. 2009, Liu and Weyers 1998).
The reinforcement corrosion process is generally divided into two time phases: the initiation (induction) period ti and the propagation period tp (Figure 1). The initiation period of the damaging mechanisms was described and validated in the earlier paper by Jendele, Šmilauer and Cervenka (2014) and results show strong influence of crack width on the transport properties and on the acceleration of the damaging mechanisms. The cracks of 0.3 mm decrease induction time approximately 6 times for carbonation and approximately 9 times for chloride ingress from sea water. Preventing macro-cracks and designing proper concrete is essential for durable concrete structures.
The presented model covers also the propagation period tp, when reinforcement corrosion takes place. During this period, reinforcement cross-sectional are decreases and is accompanied with growing corrosion products.
In the presented approach the model by Kwon, et al. (2009) for the initiation phase is combined with the effect of crack width by Liu and Weyers (1998) for the propagation period. The corrosion model is combined with the mechanical model for concrete nonlinear behaviour by Cervenka and Papanikolaou (2008).
The validation as well as more details about the individual components of the presented models is described in Hájková et al. (2019) for the corrosion model and in Cervenka and Papanikolaou (2008) for the mechanical model.
For practical application these models are used together within the digital twin concept and using the global safety formats for nonlinear analysis according to Model Code 2010 (2011).
A safety check of reinforced concrete structures for the ultimate limit states is performed by the design condition requiring that design resistance is greater than design action:
Fd < Rd (1)
In which Fd , Rd are the design values of actions and resistance respectively, and the safety is handled by the global safety format. In design assisted by numerical simulations the global resistance (strength) is determined by a model based on the finite element method. The global safety format is described in Chapter 4.6 of the fib Model Code 2010. The design resistance is formulated as:
(2)
In which Rm is the mean resistance and the global safety factor reflects the uncertainty due to the random effect of material properties. is the safety factor for model uncertainty. In fib Model Code 2010 four methods are proposed for the evaluation of the design resistance Rd : full probabilistic analysis, ECOV method, EN1992-2 global factor method and partial factor method.
ECOV method proposed by Cervenka V. (2008) is a relatively simple method, but is able to consider the aleatory uncertainty in the input parameters. It is based on the idea that the random distribution of resistance due to material, which is described by the coefficient of variation Vm, can be estimated from mean Rm and characteristic values Rm of resistance. The underlying assumption is that random distribution of resistance is according to the lognormal distribution, which is typical for the structural resistance. Considering these assumptions the coefficient of variation Vm can be expressed as:
(3)
Then the global safety factor γR of resistance can be calculated as:
(4)
Where αR is the sensitivity factor for resistance (as defined by FORM) and β is the reliability index. The above procedure enables to estimate the safety of resistance in a rational way, based on the principles of reliability accepted by the codes. Appropriate code provisions can be used to identify these parameters. For instance in the case of Eurocode EN 1990, typical values are β = 3.8 (50 years) and αR = 0.8, which corresponds to the failure probability Pf = 0.001. The global resistance factor is then:
(5)
The main task in this method, is the determination of the mean and characteristic values of resistance Rm , Rk. They can be calculated by two separate nonlinear analyses using mean and characteristic values of the input material parameters, respectively.
The method is general and reliability level β and distribution type can be changed if required. It can capture different types of failure and the sensitivity to a random variation of the material parameters is automatically included. This method requires two separate non-linear analyses.
ATENA software (Cervenka et al. 2020) is using a multi-physics approach for mechanics and transport. It predicts induction time and extent of corrosion for chloride ingress, and calculates remaining steel area. The mechanical behavior and concrete cracking is simulated using the fracture-plastic model of Cervenka et al. (1998) and Cervenka and Papanikolaou (2008). This model combines plasticity based model for compresive failure and smeared crack model with tensile softening and crack band approach for tension (Figure 2). The reinforcement corrosion is evaluated based on the parameters of the surrounding environment that are specified as a special boundary condition as shown in Figure 3. Figure 3 shows a simple example of a short cantilever whose bottom surface is subjected to chlorides. Mechanical load initiated cracks starting at the bottom surface. For each reinforcement, the closest distance to the surface subjected to chlorides is calculated. The initiation phase as well as the subsequent corrosion phases are evaluated assuming a 1D transport process along this closest distance considering also the width of a possible surface crack. Based on the amount of corrosion, the effective reinforcement area is reduced, which can directly effect the load carrying capacity or the deflections of the numerical model. This approach can simulate the effect of structural degradation in a very effective and efficient way.
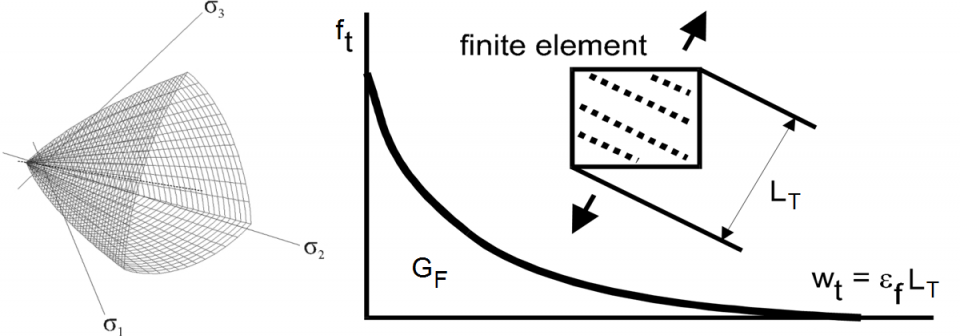
Figure 2. (left) three-parameter Menetrey and Willam failure criterion for compression, (right) crack band and tensile softening model for tension
The initiation period covers the time before the concentration of chlorides exceeds a critical value in the place of reinforcement. One dimensional chloride transient ingress into concrete, with an initially zero chloride content, can be described according to Kwon et al. (2009) as:
(6)
Where Cs is the chloride content at surface in [kg/m3], Dm(t) is the mean (averaged) diffusion coefficient at time t [m2/s], x is the distance from the surface in [m] and f(w) introduces acceleration by cracking (equals to one for a crack-free concrete). Cs and C(x,t) can be related to a concrete volume or to a binder mass. The model is in detail described in the previous paper by Hájková et al (2019).
The propagation phase is controlled by the corrosion rate. For chloride ingress it is dependant on the corrosion current density icorr [µA/cm2] and on chlorides concentration in the concrete. The model predicts the amount of corroded steel during the propagation period tp, which is governed by Faraday’s law according to Liu and Weyers (1998) by the following formula:
Where is the average corrosion rate in the radial direction [µm/year], icorr is corrosion current density [µA/cm2] and t is calculated time after the end of induction period [years]. By integration of Eq. (2), we obtain the corroded depth for 1D propagation xcorr . Rcorr is a parameter, which depends on the type of corrosion [-], uniform corrosion (carbonation) Rcorr = 1, pitting corrosion (chlorides) Rcorr = <2; 4> according to Gonzales et al. (1995) or Rcorr = <4; 5.5> according to Darmawan and Stewart (2007). d(t) is the evolution of a bar diameter in time t, dini is initial bar diameter [mm], ψ is uncertainty factor of the model [-], mean value ψ = 1 and xcorr is the total amount of corroded steel. The corrosion rate for chlorides is affected by concentration of chlorides in the concrete. The calculation of the corrosion current density was formulated by Liu and Weyer’s (1998) model:
Where icorr is the corrosion current density [µA/cm2], Ct is the total chloride content [kg/m3 of concrete] at the reinforcement location, which is determined from 1D non-stationary transport, T is temperature at the depth of reinforcement [K], Rc is the ohmic resistance of the concrete cover [Ω] (Liu 1996) and t is the time after the initiation [years].
The application of the presented approach is demonstrated on an example of Vogelsang bridge in Germany. The monitoring of this bridge was performed as a part of the international Eurostars-2 project E!10925 ‘cyberBridge‘“. It is a concrete bridge over the Neckar River in the city of Esslingen, Germany. It is a major part of the city’s infrastructure with a high impact on the regional traffic. The bridge consists of eight partial structures built in three different construction types. The bridge was built between the years of 1971 and 1973. The total length is approx. 595m and it has a total area of 9,744m² including ramps. Overview of the structure is shown in Figure 4.
During the last major check, many damages have been detected, that influence the structural safety, the safety to traffic and the durability. Due to the damages, refurbishment was urgently needed.
An important element of structural health assessment is the structural monitoring. A monitoring system in this case was placed on a part of the bridge, which is indicated by the red circle in the right bottom corner of Figure 4. This part of the bridge was used as a pilot project to evaluate the capabilities of the proposed approach. It is a two-span concrete superstructure with a total length of 27 m. A non-prestressed reinforced concrete beam is supported as a continuous beam with two spans of 13.8 and 13.2 m. Height of the beam is 0.6 m. A so called iBWIM monitoring system was used as developed by Petschacher (2010) and further extended and enhanced during the ’cyberBridge’ project. Monitoring spiders were placed on the bottom side of the slab. Each spider consists of five iBWIM sensors and one data collector. The sensor ensemble consists of one laser rangefinder; five strain gauges arranged in a row transverse to the road; and two strain gauges which are placed on either side of the row. The gauges in the row perform the actual measurement; the two adjacent gauges are used for triggering a measurement and estimating the speed of the vehicle; the laser rangefinder is used to detect and localize the vehicle axles. The group of sensors produce just one average value of micro-strain on each side of the slab. Both measuring spiders are shown in Figure 5 and Figure 6.
The monitoring was performed over an uninterrupted period lasting from Jan. 16 – Mar. 17, 2019, i.e. over 61 days. The iBWIM monitoring system provides valuable information for the durability assessment of the entire bridge including the other parts like the main river bridge. The system can provide important results like the number of heavy vehicles (trucks) crossing the bridge, the typical gross weight of the trucks, typical length of the trucks and number of axles and their weight or probability distribution of the loading events.
The monitoring data were used for the calibration of the numerical model developed in the software ATENA (Cervenka et al. 2020). The symmetric half of the bridge was modelled because of symmetry and the connection between two slabs in the middle of the bridge was neglected. The finite element mesh consisted of hexahedra quadratic isoparametric elements with the typical size of about 0,5 m. The bridge is modelled by solid elements reinforced by reinforcing steel bars (shown in Figure 7 and Figure 8). Figure 7 also shows the model of the passing truck, which was used for the model calibration using the heaviest vehicles as detected by the iBWIM monitoring system.
Figure 8. Overview on the reinforcement in the concrete slab showing the detail of the reinforcement arrangement above the middle piers
Initial material parameters were set based on structural diagnostic and on the original bridge design specification. In the original design the concrete B450 (original German notation) was assumed, while the compressive tests on drilled cores show the compressive strength of fc,cyl = 35,5 MPa and elastic modulus Ec = 33,3 MPa. This initial parameters were used in a parametric and optimization study to identify the most suitable material parameters for the subsequent durability and bridge life prediction analysis. The optimization was performed using the monitoring data obtained during the monitoring process as described in Section ‘Monitoring’. The initial analyses showed that cracks must exists in the bridge in order to match the measured strains, therefore the main optimization parameters were selected to be tensile strength and fracture energy . The final optimized set of parameters is shown in Table 1.
Table 1. Optimized concrete material parameters
|
Material parameter |
Value |
|
Young´s modulus E [GPa] |
33.3 |
|
Poisson´s ratio ν [-] |
0.2 |
|
Compressive strength fc [MPa] |
-35.5 |
|
Tensile strength ft [MPa] |
3.24 |
|
Fracture energy GF [N/m] |
144 |
|
Plastic strain at compressive strength εcp [-] |
-0.00123 |
|
Critical compressive displacement wd [mm] |
-0.5 |
|
Reduction of compressive strength due to cracks [-] |
0.8 |
Figure 9 shows the typical deflection and crack development during the simulation of a two axle truck passing with gross vehicle weight of 27.6 tons. In this case the monitoring system detected the strain of 77 μstrains (group 203) during the truck passing and 30 μs on the neighboring lane (group 204) (see Figure 6). In the optimized numerical analysis the calculated strains at the location of group 203 sensors was 74 μs and 43 μs at sensor group 204. The average error was about 19% from the monitoring and numerical results for the optimized set of parameters.
The calibrated model according to the previous section was used for a prognosis of structural service life using the durability model described in under ‘Global safety formats for ULS and simulation based design’. The same numerical model was used as described in the previous section. In the durability assessment, the bridge is loaded by the permanent load and average life/traffic load as determined by the monitoring data in Section ‘Monitoring’. Then it is subjected to the environmental actions: chlorides: Dref = 1.2e-7 m2/day, tDref = 3650 days, mcoeff = 0.37, tmcoeff = 10950 days, Clcrit = 0.004, ft,ch = 3.2 MPa, wd = 0.001 m, pitting corrosion Rcorr = 2. Chloride surface concentration Cs was applied differently for the top surface Cs = 0.009 and for bottom surface Cs = 0.0055. The corrosion rate after concrete spalling was assumed at 35 μm/year.
All models have been calculated with two sets of material parameters (characteristic and mean) such that it is possible to applied the global resistance method ECOV as described in Section ‘Global safety formats for ULS and simulation based design’.
The environmental action of chloride ingress was calculated for several duration times: 25, 50, 75, 100 and 150 years. At these times the numerical models are loaded by the most critical ULS load combination. The load is then increased all the way up to failure (see Figure 11). This is accomplished by using the Arc-length nonlinear solution methods (Crisfield 1983), which allows for automatic reduction of the applied load such that a peak load can be detected in load controlled numerical analysis. Figure 12 shows the overloading curves at different ages of the bridge for the case with characteristic material properties.
The main results from the durability analysis for the case using mean material properties are shown in Figure 13. In this figure, the time development of structural capacity is evaluated using the ECOV method (Section ‘Global safety formats for ULS and simulation based design’). It shows that the design resistance (solid red line) will drop below the design load level (ULS curve) in 110 years. This number can be interpreted as the service life of the structure. If proper rehabilitation is performed in this period, the service life can be even extended above this time. The current age of the structure was 45 years, so this would mean additional 50-60 years. This was more than the expected life of 15-20 years based mainly on traditional visual observation and expert judgement.
Realistic simulation of structural response during its service life as well as critical load combinations is the concept embraced currently mainly by mechanical engineers. Due to the introduction of global safety formats in model code 2010 as well as in the new generation of Eurocodes opens a door for adopting the ‘digital twin concept’ also in the construction industry.
In the presented example the numerical simulation was combined with an advanced monitoring system to develop a calibrated numerical model of an existing bridge structure. The calibrated numerical model was used to perform durability assessment of the investigated bridge and predict its service life considering the structural degradation due to corrosion. In this pilot investigation is was possible to prove the service life of additional 30-45 years over the initially expected period. In practise it is critical to complement numerical predictions, by extensive on-site investigation and monitoring program.
Acknowledgements: The monitoring program was part of an international Eurostars-2 project E! 10925 “cyberBridge”. The optimization of material parameters was using the tools and methods developed under the project supported by Technological Agency of Czech Republic - TF06000016, Advanced system for monitoring, diagnosis and reliability assessment of large-scale concrete infrastructures.
For more information on the Atena software, go to www.cervenka.cz/products/atena/.