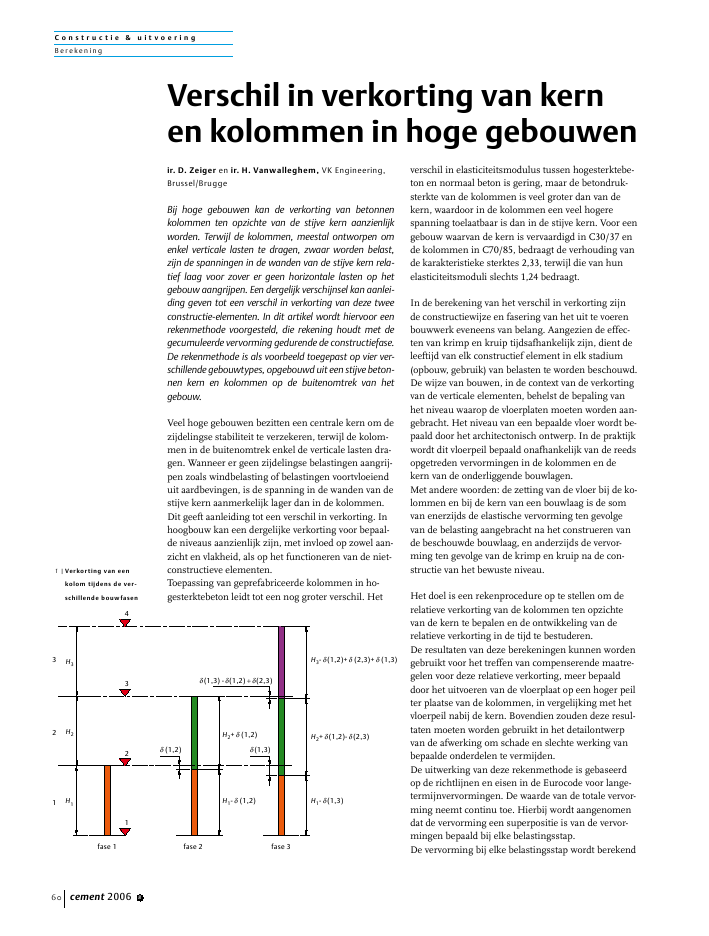
C o n s t r u c t i e & u i t v o e r i n gB erekening60 cement 2006 8ir. D. Zeiger en ir. H. Vanwalleghem, VK Engineering,Brussel/BruggeBij hoge gebouwen kan de verkorting van betonnenkolommen ten opzichte van de stijve kern aanzienlijkworden. Terwijl de kolommen, meestal ontworpen omenkel verticale lasten te dragen, zwaar worden belast,zijn de spanningen in de wanden van de stijve kern rela-tief laag voor zover er geen horizontale lasten op hetgebouw aangrijpen. Een dergelijk verschijnsel kan aanlei-ding geven tot een verschil in verkorting van deze tweeconstructie-elementen. In dit artikel wordt hiervoor eenrekenmethode voorgesteld, die rekening houdt met degecumuleerde vervorming gedurende de constructiefase.De rekenmethode is als voorbeeld toegepast op vier ver-schillende gebouwtypes, opgebouwd uit een stijve beton-nen kern en kolommen op de buitenomtrek van hetgebouw.Veel hoge gebouwen bezitten een centrale kern om dezijdelingse stabiliteit te verzekeren, terwijl de kolom-men in de buitenomtrek enkel de verticale lasten dra-gen. Wanneer er geen zijdelingse belastingen aangrij-pen zoals windbelasting of belastingen voortvloeienduit aardbevingen, is de spanning in de wanden van destijve kern aanmerkelijk lager dan in de kolommen.Dit geeft aanleiding tot een verschil in verkorting. Inhoogbouw kan een dergelijke verkorting voor bepaal-de niveaus aanzienlijk zijn, met invloed op zowel aan-zicht en vlakheid, als op het functioneren van de niet-constructieve elementen.Toepassing van geprefabriceerde kolommen in ho-gesterktebeton leidt tot een nog groter verschil. Hetverschil in elasticiteitsmodulus tussen hogesterktebe-ton en normaal beton is gering, maar de betondruk-sterkte van de kolommen is veel groter dan van dekern, waardoor in de kolommen een veel hogerespanning toelaatbaar is dan in de stijve kern. Voor eengebouw waarvan de kern is vervaardigd in C30/37 ende kolommen in C70/85, bedraagt de verhouding vande karakteristieke sterktes 2,33, terwijl die van hunelasticiteitsmoduli slechts 1,24 bedraagt.In de berekening van het verschil in verkorting zijnde constructiewijze en fasering van het uit te voerenbouwwerk eveneens van belang. Aangezien de effec-ten van krimp en kruip tijdsafhankelijk zijn, dient deleeftijd van elk constructief element in elk stadium(opbouw, gebruik) van belasten te worden beschouwd.De wijze van bouwen, in de context van de verkortingvan de verticale elementen, behelst de bepaling vanhet niveau waarop de vloerplaten moeten worden aan-gebracht. Het niveau van een bepaalde vloer wordt be-paald door het architectonisch ontwerp. In de praktijkwordt dit vloerpeil bepaald onafhankelijk van de reedsopgetreden vervormingen in de kolommen en dekern van de onderliggende bouwlagen.Met andere woorden: de zetting van de vloer bij de ko-lommen en bij de kern van een bouwlaag is de somvan enerzijds de elastische vervorming ten gevolgevan de belasting aangebracht na het construeren vande beschouwde bouwlaag, en anderzijds de vervor-ming ten gevolge van de krimp en kruip na de con-structie van het bewuste niveau.Het doel is een rekenprocedure op te stellen om derelatieve verkorting van de kolommen ten opzichtevan de kern te bepalen en de ontwikkeling van derelatieve verkorting in de tijd te bestuderen.De resultaten van deze berekeningen kunnen wordengebruikt voor het treffen van compenserende maatre-gelen voor deze relatieve verkorting, meer bepaalddoor het uitvoeren van de vloerplaat op een hoger peilter plaatse van de kolommen, in vergelijking met hetvloerpeil nabij de kern. Bovendien zouden deze resul-taten moeten worden gebruikt in het detailontwerpvan de afwerking om schade en slechte werking vanbepaalde onderdelen te vermijden.De uitwerking van deze rekenmethode is gebaseerdop de richtlijnen en eisen in de Eurocode voor lange-termijnvervormingen. De waarde van de totale vervor-ming neemt continu toe. Hierbij wordt aangenomendat de vervorming een superpositie is van de vervor-mingen bepaald bij elke belastingsstap.De vervorming bij elke belastingsstap wordt berekendVerschil in verkorting van kernen kolommen in hoge gebouwen1231234fase 1 fase 2 fase 3H1H2H3H1- (1,2)H2+ (1,2) (1,2)H1-(1,3)H2+(1,2)-(2,3)H3-(1,2)+ (2,3)+ (1,3)(1,3)(1,3) -(1,2) +(2,3)1 |Verkorting van eenkolom tijdens de ver-schillende bouwfasenC o n s t r u c t i e & u i t v o e r i n gB erekeningcement 2006 8 61als functie van de ouderdom van het beton van elkverticaal constructief element en de tijdsduur tussentwee belastingsstadia.De belasting op elke bouwlaag wordt in twee delenopgesplitst:1. eigen gewicht van de constructie-elementen;2. de permanente belasting en het quasi-permanentedeel van de mobiele belasting.De berekeningsmethode wordt uitgewerkt met be-hulp van een hiervoor ontwikkeld computerprogram-ma.W i s k u n d i g e b e n a d e r i n gDe constructiewijze is afgebeeld in figuur 1. Volgensdeze methode worden de te bouwen bouwlagen uitge-voerd tot op een voorgeschreven absoluut niveau. Inde figuur betekent Hide hoogte van het ideniveau vol-gens het architectonisch ontwerp en (i,j) de totaleverkorting van een kolom op het ideniveau in bouwfa-se j.In de eerste fase wordt de kolom op de eerste bouw-laag opgetrokken en belast door zijn eigen gewicht. Inde tweede fase wordt deze kolom belast door de vloer-plaat van de tweede bouwlaag, wat aanleiding geeft toteen verkorting (1,2). Deze verkorting omvat zowelde elastische verkorting, als de verkorting ten gevolgevan de krimp die is opgetreden na uitvoering van dekolom. In deze fase wordt ook de kolom van de twee-de bouwlaag geplaatst met een lengte van H2+ (1,2),teneinde het correcte peil van de derde bouwlaag tebereiken. Deze hoogte komt overeen met H1+ H2(fig.1). In de derde fase wordt de derde bouwlaag uitge-voerd, waarbij de verkorting (1,3) naast de elastischeverkorting en de krimp, eveneens de kruip bevat tengevolge van de belasting van de tweede bouwlaag.Dit proces gaat voor de andere bouwlagen continudoor zoals voorgesteld in figuur 1, waarbij de bijko-mende belastingen (permanent + mobiel) vanaf eenbepaald tijdstip op de bouwlagen aangrijpen.Veronderstel dat elke bouwfase overeenstemt met derespectievelijke bouwlaag, dan kan de lengte van elkekolom in een bouwfase j als volgt worden uitgedrukt:(1)h0 j, H (i,j) ? (i,j ? 1)j i 1=j 1? i 1=j 2?+=hj Hj i j,( ) (i,j ? 1) ? ( j,k)i 1=j 2??i 1=j 1?+= 1 t,( ) (Pi) + (Q i) + (Pi; (tp,i,t)) + (Q i; (tq,i,t)) + (t1,t)e 1,i 2=N e 1,i 2=M cr 1,i 2=N cr,1 sh,1i 2=M=waarbij Hjde hoogte voorstelt van een bouwlaag j vol-gens het architectonisch ontwerp en h0,jde fabricage-lengte van de kolom.De hoogte van dit element in een volgende bouwfasek, na het aangrijpen van de vervormingen, wordt uit-gedrukt als:(2)h0 j, H (i,j) ? (i,j ? 1)j i 1=j 1? i 1=j 2?+=hj Hj i j,( ) (i,j ? 1) ? ( j,k)i 1=j 2??i 1=j 1?+= 1 t,( ) (Pi) + (Q i) + (Pi; (tp,i,t)) + (Q i; (tq,i,t)) + (t1,t)e 1,N e 1,M cr 1,N cr,1 sh,1M=Deze vervorming wordt gedefinieerd als de totale ver-korting van een kolom op de idebouwlaag tijdensbouwfase j, met inbegrip van krimp en kruip. De be-rekeningsmethode van deze waarde is gebaseerd opENV1992-1-1. Volgens deze formulering kan de totalevervorming worden voorgesteld door een superpositievan:? de elastische vervorming e;? de krimp sh;? de kruip cr. = e+ sh+ cr(3)Volgens deze definitie kunnen de volgende verkortin-gen worden gedefinieerd:? (1,1): de kolom van de eerste bouwlaag is niet be-last in deze fase;? (1,2) = e,1(P2) + sh,1(t1,t2);waarin:e,1(P2) is de elastische vervorming van de kolomop de eerste bouwlaag ten gevolge van debelasting van de tweede bouwlaag;sh,1(t1,t2) is de krimp van de kolom tussen t1(de tijdtussen het oprichten van de kolom van deeerste bouwlaag) en t2, het tijdstip van hetuitvoeren van de tweede bouwlaag.2 |Ellypse building metstandaardplattegrondabC o n s t r u c t i e & u i t v o e r i n gB erekening62 cement 2006 8-35-30-25-20-15-10-50-2 0 2 4 6 8 10 12-35-30-25-20-15-10-50-2 0 2 4 6 8 10 12bouwlaagverkortingkolom(mm)bouwlaagverkortingkern(mm)-12-10-8-6-4-20-2 0 2 4 6 8 10 12bouwlaagrelatieveverkortingkolomt.o.v.kern(mm)In de derde bouwfase geldt de volgende vergelijking:(1,3) = e,1(P2)+ e,1(P3)+cr,1(P2, (t2,t3))+ sh,1(t1,t3)Naast het aandeel van de elastische vervorming en dekrimp, verschijnt hier het aandeel van de kruip. Decomponent cr,1(P2, (t2,t3)) is een functie van de be-lasting van de tweede bouwlaag P2en de kruipco?ffi-ci?nt . De kruipco?ffici?nt is een functie van de ou-derdom van het beton op t2(de tijd waarop debelasting P2wordt aangebracht) en de ouderdom vanhet beton op t3.Veralgemening van deze uitdrukking voor de vervor-ming van de kolommen van de eerste bouwlaag, vooreen gegeven tijdstip t en voor de opgebrachte belastin-gen Pi, geeft:h0 j, H (i,j) ? (i,j ? 1)j i 1=j 1? i 1=j 2?+=hj Hj i j,( ) (i,j ? 1) ? ( j,k)i 1=j 2??i 1=j 1?+= 1 t,( ) (Pi) + (Q i) + (Pi; (tp,i,t)) + (Q i; (tq,i,t)) + (t1,t)e 1,i 2=N e 1,i 2=M cr 1,i 2=N cr,1 sh,1i 2=M= n t,( ) (Pi) + (Q i) + (Pi; (tp,i;t)) + (Q i; (tq,i;t)) + (tn,t)e n,i n + 1=N e n,i n + 1=M cr n,i n + 1=N cr,n sh,ni n + 1=M=Pi Ln(4)H (i,j) ? (i,j ? 1)j i 1=j 1? i 1=j 2?+= i j,( ) (i,j ? 1) ? ( j,k)i 1=j 2??1=1?t) (Pi) + (Q i) + (Pi; (tp,i,t)) + (Q i; (tq,i,t)) + (t1,t)e 1,i 2=N e 1,i 2=M cr 1,i 2=N cr,1 sh,1i 2=M=t) (Pi) + (Q i) + (Pi; (tp,i;t)) + (Q i; (tq,i;t)) + (tn,t)e n,i n + 1=N e n,i n + 1=M cr n,i n + 1=N cr,n sh,ni n + 1=M=waarin:N is de hoogste bouwlaag opgetrokken op tijd-stip t;M is de bovenliggende bouwlagen belast methun belasting op tijdstip t;t is de tijd in dagen;Piis het eigengewicht van de idebouwlaag;Qiis de permanente belasting en het quasi-per-manente deel van de mobiele belasting op deidebouwlaag;tp,iis het tijdstip waarop Piaangrijpt;tq,iis het tijdstip waarop Qiaangrijpt;(t1;t) is de kruipco?ffici?nt, functie van de ouder-dom van de kolom op de onderste bouwlaagop t1en de ouderdom van deze kolom op tijd-stip t.Verdere uitwerking van uitdrukking (4) voor een ko-lom op de ndebouwlaag levert de volgende uitdruk-king (5):h0 j, H (i,j) ? (i,j ? 1)j i 1=j 1? i 1=j 2?+=hj Hj i j,( ) (i,j ? 1) ? ( j,k)i 1=j 2??i 1=j 1?+= 1 t,( ) (Pi) + (Q i) + (Pi; (tp,i,t)) + (Q i; (tq,i,e 1,i 2=N e 1,i 2=M cr 1,i 2=N cr,1i 2=M= n t,( ) (Pi) + (Q i) + (Pi; (tp,i;t)) + (Q i; (tq,i;e n,i n + 1=N e n,i n + 1=M cr n,i n + 1=N cr,ni n + 1=M=e n, Pi( )Pi LnEc tp i, tp n,? t0 n,+( ) An=crP L t0 t,( ) Ec 28, Ac=(5)h0 j, H (i,j) ? (i,j ? 1)j i 1=j 1? i 1=j 2?+=hj Hj i j,( ) (i,j ? 1) ? ( j,k)i 1=j 2??i 1=j 1?+= 1 t,( ) (Pi) + (Q i) + (Pi; (tp,i,t)) + (Q i; (tq,i,t)) + (t1,t)e 1,i 2=N e 1,i 2=M cr 1,i 2=N cr,1 sh,1i 2=M= n t,( ) (Pi) + (Q i) + (Pi; (tp,i;t)) + (Q i; (tq,i;t)) + (tn,t)e n,i n + 1=N e n,i n + 1=M cr n,i n + 1=N cr,n sh,ni n + 1=M=e n, Pi( )Pi LnEc tp i, tp n,? t0 n,+( ) An=crP L t0 t,( ) Ec 28, Ac=De elastische verkorting van een kolom op de ndebouwlaag ten gevolge van de belasting Piis gelijk aan:(6)h0 j, H (i,j) ? (i,j ? 1)j i 1=j 1? i 1=j 2?+=hj Hj i j,( ) (i,j ? 1) ? ( j,k)i 1=j 2??i 1=j 1?+= 1 t,( ) (Pi) + (Q i) + (Pi; (tp,i,t)) + (e 1,i 2=N e 1,i 2=M cr 1,i 2=N cr,1i 2=M= n t,( ) (Pi) + (Q i) + (Pi; (tp,i;t)) + (e n,i n + 1=N e n,i n + 1=M cr n,i n + 1=N cr,ni n + 1=M=e n, Pi( )Pi LnEc tp i, tp n,? t0 n,+( ) An=crP L t0 t,( ) Ec 28, Ac=waarin:Piis het eigengewicht van de idebouwlaag;An= Ac+ nAs; de equivalente dwarsdoorsnede,die rekening houdt met het verschil in stijf-heid tussen beton en staal;Acis de dwarsdoorsnede van het beton;Asis de dwarsdoorsnede van het wapeningsstaal;n = Es/ Ec; met Esen Ecrespectievelijk de elasti-citeitsmodulus van staal en beton;Lnis de hoogte van de kolom op de ndebouwlaag.Voor Qigeldt een met formule (6) overeenkomstigeformule.De invloed van de ouderdom van het beton werd inge-voerd in (6) als de som van de ouderdom van het be-ton op het moment van de uitvoering van de ndebouwlaag en de tijd tussen de constructie van de idebouwlaag (aangeduid met tp,i) en de constructie van dendebouwlaag (aangeduid met tp,n). In het geval de ko-lom ter plaatse werd gestort, is t0,ngelijk aan nul.3 |Gebouw Au einde bouwfasen twee jaar na aanvangconstructies vijf jaar na aanvangconstructie6 tien jaar na aanvangconstructiel zeventig jaar na aanvangconstructieabcC o n s t r u c t i e & u i t v o e r i n gB erekeningcement 2006 8 63bouwlaagverkortingkolom(mm)bouwlaagverkortingkern(mm)bouwlaagrelatieveverkortingkolomt.o.v.kern(mm)-60-50-40-30-20-100-3 2 7 12 17 22-60-50-40-30-20-100-3 2 7 12 17 22-25-20-15-10-50-3 2 7 12 17 22De vervorming ten gevolge van kruip wordt uitge-drukt door:(7)e n, Pi( )Pi LnEc tp i, tp n,? t0 n,+( ) An=crP L t0 t,( ) Ec 28, Ac=waarbij Ec,28de elasticiteitsmodulus is van het betonmet een ouderdom van 28 dagen en (t0,t) de kruip-co?ffici?nt, die functie is van de ouderdom van het be-ton op het moment dat de belasting P aangrijpt (aan-geduid met t0) en de ouderdom van het beton optijdstip t. Deze kruipco?ffici?nt wordt berekend aande hand van ENV 1992 waarbij, naast de betonouder-dom op t0en t, de co?ffici?nt afhankelijk is van dedruksterkte van het beton, het cementtype, de dwars-doorsnede van het betonelement en de relatieve voch-tigheid. De waarde van wordt voor elke bouwlaagafzonderlijk bepaald.De vervormingen van de kolommen of de wandenvan een bepaalde bouwlaag ten gevolge van de krimpwordt uitgedrukt door:sh= esh(t1,t2)?H (8)waarin H de verdiepingshoogte is en esh(t1,t2) de rekten gevolge van de krimp tussen t1en t2, zie ENV1992. De waarde van eshwordt bepaald als functie vande ouderdom van het beton aan het begin en aan heteinde van de beschouwde periode, de vorm van dedwarsdoorsnede, de druksterkte van het beton, hetcementtype en de relatieve vochtigheid.V o o r b e e l d e n e n r e s u l t a t e nAls voorbeeld werd de Ellypse Building in Brussel ge-nomen (foto 2). Deze hoogbouw bestaat uit 22 boven-grondse en drie ondergrondse verdiepingen.Het gebouw bestaat uit een centrale kern en ronde ko-lommen (?. 600 mm) in hogesterktebeton op de bui-tenomtrek. De andere voorbeelden zijn drie variantenvan dit gebouw, waarbij het aantal bouwlagen, de be-tondruksterkte en de dwarsdoorsnede van de kolom-men werden gewijzigd. De elasticiteitsmodulus vande wapening (210 000 N/mm?) en de relatieve voch-tigheid van 70% zijn voor de vier voorbeelden gelijk.1. Gebouw A: 15 verdiepingen, kolommen en stijvekern C25/30;2. Gebouw B: 26 verdiepingen, kolommen C40/50,stijve kern C25/30;3. Gebouw C: het origineel concept van de EllypseBuilding, 26 verdiepingen, kolommenin hogesterktebeton, C50/60 voor dehoogste niveaus en C70/85 voor de on-derste verdiepingen;4. Gebouw D: 40 verdiepingen, kolommen C45/55tot C90/105, stijve kern C30/37.Voor elk van de voorbeelden A tot en met D werdende dwarsdoorsnede van de kolommen en de wape-ning berekend voor de verticale belasting, de stijvekern voor de buigende momenten ten gevolge van dehorizontale belastingen.Aangenomen is dat elke vloer als volgt wordt belast:? belastingsfase 1: het eigen gewicht van de construc-tieve elementen overeenkomstig de bouwfasen;? belastingsfase 2: de permanente en mobiele belas-ting vermenigvuldigd met hun respectievelijke re-ductiefactoren, waarbij de ene factor een functie isvan het aantal bovenliggende bouwlagen ten op-zichte van de beschouwde vloer en de andere vanhet quasi-permanente deel van de mobiele belas-ting (conform ENV 1991).De resultaten werden uitgewerkt voor de volgende vijfperiodes:1. op het einde van de constructie van het gebouw;2. twee jaar na aanvang van de constructie;3. vijf jaar na aanvang van de constructie;4. tien jaar na aanvang van de constructie;5. zeventig jaar na aanvang van de constructie, welkevolgens ENV 1992 de tijd is waarbij de kruip vanhet beton als be?indigd kan worden veronder-steld.4 |Gebouw Bu einde bouwfasen twee jaar na aanvangconstructies vijf jaar na aanvangconstructie6 tien jaar na aanvangconstructiel zeventig jaar na aanvangconstructieabcC o n s t r u c t i e & u i t v o e r i n gB erekening64 cement 2006 8bouwlaagverkortingkolom(mm)bouwlaagverkortingkern(mm)bouwlaagrelatieveverkortingkolomt.o.v.kern(mm)-60-50-40-30-20-100-3 2 7 12 17 22-60-50-40-30-20-100-3 2 7 12 17 22-30-25-20-15-10-50-3 2 7 12 17 22De resultaten zijn aangegeven in de figuren 3 tot enmet 6. Deze tonen aan dat de verplaatsing van de bo-venste vloerplaat nul is. Dit vindt zijn oorzaak in hetfeit dat elke bouwlaag wordt uitgevoerd volgens zijnvoorgeschreven peil, onafhankelijk van de vervormin-gen van de kolommen en de stijve kern op de onder-gelegen niveaus. De verschil in verkorting op de laat-ste bouwlaag is nul doordat de kolommen en de kern(theoretisch) tezelfdertijd werden uitgevoerd.De maximale relatieve verkorting bedraagt:? voor gebouw A: 11 mm;? voor gebouw B: 20 mm;? voor gebouw C: 29 mm;? voor gebouw D: 42 mm.De maximale waarden van de absolute en de relatieveverkortingen worden nooit bereikt op de hoogstebouwlaag. De maximale waarden van de relatieve ver-korting zijn terug te vinden tussen:? de 7deen 9debouwlaag in gebouw A;? de 11deen 14debouwlaag in gebouw B;? de 11deen 15debouwlaag in gebouw C;? de 21steen 25stebouwlaag in gebouw D.De maximumwaarde voor de relatieve verkortingwordt niet noodzakelijk bereikt na zeventig jaar:voor gebouw B wordt de maximale relatieve verkor-ting reeds bereikt na tien jaar. Het verschil tussendeze verkorting en de maximale relatieve verkortingna vijf of na zeventig jaar bedraagt slechts enkeletienden van een millimeter. Voor gebouw C en Dwordt de maximale verkorting bereikt na vijf jaar.De waarde van de maximale relatieve verkorting tenopzichte van een veldoverspanning wordt berekendmet de veldoverspanning van de Ellypse Building,zijnde 6,50 m. Deze relatieve waarde bedraagt voor:? gebouw A: 1/591;? gebouw B: 1/325;? gebouw C: 1/224;? gebouw D: 1/155.Dit zijn waarden die worden verkregen indien geenmaatregelen worden genomen om de relatieve verkor-ting te compenseren.Het proces van de verkorting duurt lang, maar degrootte van de verkorting en in het bijzonder de rela-tieve verkorting vermindert met de tijd.De relatieve verkorting na twee jaar bedraagt voor:? gebouw A 72% van de maximale relatieve ver-korting;? gebouw B 90% van de maximale relatieve ver-korting;? gebouw C 93% van de maximale relatieve ver-korting;? gebouw D 92% van de maximale relatieve ver-korting.Echter op het einde van de constructie van het ge-bouw bedraagt de differenti?le verkorting slechts:? gebouw A 38% van de maximale relatieve ver-korting;? gebouw B 61% van de maximale relatieve ver-korting;? gebouw C 66% van de maximale relatieve ver-korting;? gebouw D 48% van de maximale relatieve ver-korting.Berekeningen van de relatieve verkorting met ver-waarlozing van de krimp tonen aan dat het aandeelvan de krimp ten aanzien van de totale relatieve ver-kortingen gemiddeld:? 15% bedraagt in gebouw A;? 7% bedraagt in gebouw B en C;? 14% bedraagt in gebouw D.5 |Gebouw Cu einde bouwfasen twee jaar na aanvangconstructies vijf jaar na aanvangconstructie6 tien jaar na aanvangconstructiel zeventig jaar na aanvangconstructieabcC o n s t r u c t i e & u i t v o e r i n gB erekeningcement 2006 8 65bouwlaagverkortingkolom(mm)bouwlaagverkortingkern(mm)bouwlaagrelatieveverkortingkolomt.o.v.kern(mm)-90-80-70-60-50-40-30-20-100-3 0 3 6 9 12 15 18 21 24 27 30 33 36-90-80-70-60-50-40-30-20-100-3 0 3 6 9 12 15 18 21 24 27 30 33 36-45-40-35-30-25-20-15-10-50-3 0 3 6 9 12 15 18 21 24 27 30 33 36T e n s l o t t eIn bovenstaande beschouwingen werd een bereke-ningsmethode weergegeven voor de berekening vanhet verschil in verkorting tussen de betonnen kolom-men en de betonnen stijve kern van hoge gebouwen.De vier uitgewerkte voorbeelden zijn telkens varian-ten van eenzelfde constructie. De variabele parame-ters zijn: het aantal bouwlagen, de betondruksterkteen de dwarsdoorsnede van de constructieve elemen-ten.De resultaten geven aanleiding tot de volgende con-clusies:1. De relatieve verkorting van kolommen ten opzich-te van de stijve kern kan aanzienlijk worden voorhoge gebouwen en er moet reeds bij het ontwerpvan dergelijke constructies rekening mee wordengehouden. In bepaalde gevallen is het noodzake-lijk de vloerplaten in de nabijheid van de kolom-men hoger uit te voeren dan ter hoogte van destijve kern. In de hier voorgestelde voorbeeldentreedt het grootste deel van de vervormingen optijdens de eerste twee jaar na aanvang van de con-structie. Voor gelijksoortige gebouwen moet indeze periode de nodige aandacht worden besteedaan de plaatsing van de niet-constructieve elemen-ten, teneinde schade aan deze elementen te ver-mijden.2. De grootste waarde van de relatieve verkorting be-vindt zich ongeveer op 60 ? 75% van de totalehoogte van het gebouw. Dit komt door de maniervan bouwen, waarbij elk niveau wordt uitgevoerdten opzichte van zijn vooraf gedefinieerd absoluutpeil, onafhankelijk van de optredende vervormin-gen van de ondergelegen verdiepingen tijdens deopbouw van de constructie.3. De verandering van de relatieve verkorting tussende kolommen en de stijve kern twee jaar na aan-vang van de bouwwerken, is gering voor de con-structies die hier werden geanalyseerd. Voor der-gelijke gebouwen kan worden volstaan met de tenemen compenserende maatregelen af te stellenop de relatieve vervorming, begroot na een perio-de van twee jaar.4. Het aandeel van de krimp in de totale relatieveverkorting is klein, maar niet verwaarloosbaar. Inde gemaakte voorbeelden bedroeg het gemiddeldaandeel van de krimp 7% (gebouw B en C) tot15% (gebouw A) van de totale differenti?le verkor-ting.5. Het gebruik van hogesterktebeton voor de kolom-men geeft aanleiding tot een grotere relatieve ver-korting.6. De resultaten voor een gebouw met vijftien verdie-pingen (gebouw A) tonen aan dat voor dergelijkeconstructies, of constructies met minder verdie-pingen, de relatieve verkorting tussen de kolom-men en de kern gering is. nL i t e r a t u u r1. ENV 1992-1-1 Eurocode 2: Design of concretestructures ? Part 1-1: General rules and rules forbuildings, December 1991.2. prEN 1992-1-1 Eurocode 2: Design of concretestructures ? Part 1-1: General rules and rules forbuildings, April 2003.3. ENV 1991-1 Eurocode 1: Basis of design andactions on structures ? Part 1: Basis of design,September 1994.6 |Gebouw Du einde bouwfasen twee jaar na aanvangconstructies vijf jaar na aanvangconstructie6 tien jaar na aanvangconstructiel zeventig jaar na aanvangconstructieabc