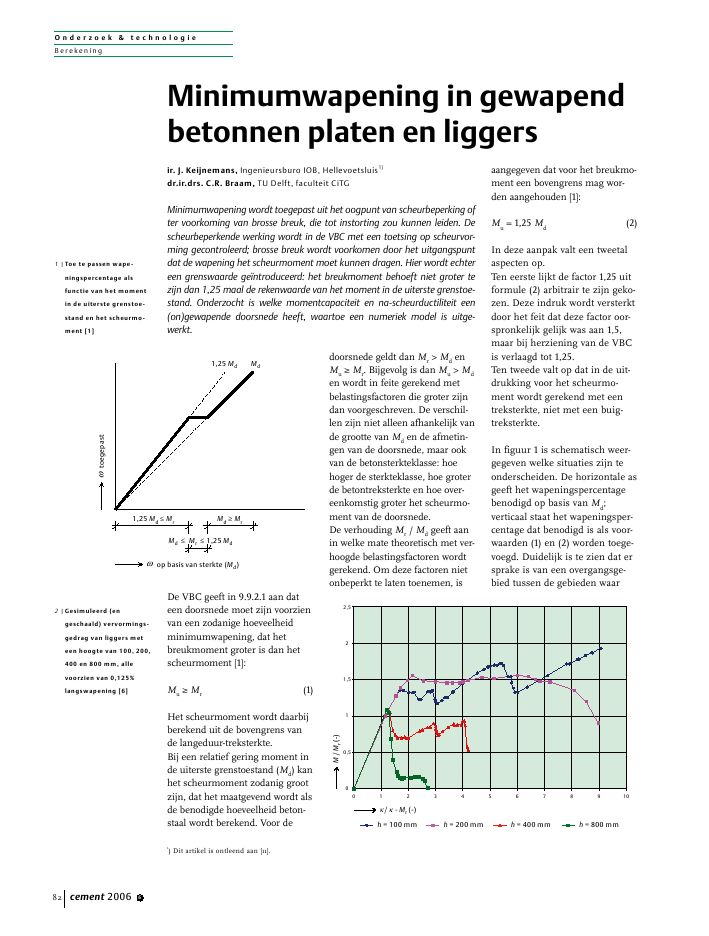
O n d e r z o e k & t e c h n o l o g i eB erekeningcement 2006 682De VBC geeft in 9.9.2.1 aan dateen doorsnede moet zijn voorzienvan een zodanige hoeveelheidminimumwapening, dat hetbreukmoment groter is dan hetscheurmoment [1]:Mu Mr(1)Het scheurmoment wordt daarbijberekend uit de bovengrens vande langeduur-treksterkte.Bij een relatief gering moment inde uiterste grenstoestand (Md) kanhet scheurmoment zodanig grootzijn, dat het maatgevend wordt alsde benodigde hoeveelheid beton-staal wordt berekend. Voor dedoorsnede geldt dan Mr> MdenMu Mr. Bijgevolg is dan Mu> Mden wordt in feite gerekend metbelastingsfactoren die groter zijndan voorgeschreven. De verschil-len zijn niet alleen afhankelijk vande grootte van Mden de afmetin-gen van de doorsnede, maar ookvan de betonsterkteklasse: hoehoger de sterkteklasse, hoe groterde betontreksterkte en hoe over-eenkomstig groter het scheurmo-ment van de doorsnede.De verhouding Mr/ Mdgeeft aanin welke mate theoretisch met ver-hoogde belastingsfactoren wordtgerekend. Om deze factoren nietonbeperkt te laten toenemen, isaangegeven dat voor het breukmo-ment een bovengrens mag wor-den aangehouden [1]:Mu= 1,25 Md(2)In deze aanpak valt een tweetalaspecten op.Ten eerste lijkt de factor 1,25 uitformule (2) arbitrair te zijn geko-zen. Deze indruk wordt versterktdoor het feit dat deze factor oor-spronkelijk gelijk was aan 1,5,maar bij herziening van de VBCis verlaagd tot 1,25.Ten tweede valt op dat in de uit-drukking voor het scheurmo-ment wordt gerekend met eentreksterkte, niet met een buig-treksterkte.In figuur 1 is schematisch weer-gegeven welke situaties zijn teonderscheiden. De horizontale asgeeft het wapeningspercentagebenodigd op basis van Md;verticaal staat het wapeningsper-centage dat benodigd is als voor-waarden (1) en (2) worden toege-voegd. Duidelijk is te zien dat ersprake is van een overgangsge-bied tussen de gebieden waarMinimumwapening in gewapendbetonnen platen en liggersir. J. Keijnemans, Ingenieursburo IOB, Hellevoetsluis1)dr.ir.drs. C.R. Braam, TU Delft, faculteit CiTGMinimumwapening wordt toegepast uit het oogpunt van scheurbeperking ofter voorkoming van brosse breuk, die tot instorting zou kunnen leiden. Descheurbeperkende werking wordt in de VBC met een toetsing op scheurvor-ming gecontroleerd; brosse breuk wordt voorkomen door het uitgangspuntdat de wapening het scheurmoment moet kunnen dragen. Hier wordt echtereen grenswaarde ge?ntroduceerd: het breukmoment behoeft niet groter tezijn dan 1,25 maal de rekenwaarde van het moment in de uiterste grenstoe-stand. Onderzocht is welke momentcapaciteit en na-scheurductiliteit een(on)gewapende doorsnede heeft, waartoe een numeriek model is uitge-werkt.1) Dit artikel is ontleend aan [11].toegepastop basis van sterkte (Md)1,25 Md1,25 Md MrMd Mr 1,25 MdMd MrMd1 |Toe te passen wape-ningspercentage alsfunctie van het momentin de uiterste grenstoe-stand en het scheurmo-ment [1]2 |Gesimuleerd (engeschaald) vervormings-gedrag van liggers meteen hoogte van 100, 200,400 en 800 mm, allevoorzien van 0,125%langswapening [6]2,51,50,5210M/Mr(-)h = 100 mm h = 200 mm h = 400 mm/ - Mr (-)h = 800 mm 0 1 2 3 4 5 6 7 8 9 10O n d e r z o e k & t e c h n o l o g i eB erekeningcement 2006 6 83lamelMNlcfctfctongescheurdgescheurdwcrw1,25 Mden Mdmaatgevend zijn,respectievelijk links en rechtsvan dit overgangsgebied.In Eurocode 2 wordt een aanpakgevolgd die vergelijkbaar is met deaanpak in de VBC, zij het dat eenfactor 1,2 in de uitdrukking voor debovengrens (vergelijk formule (2))wordt gebruikt [2]. Ook in de Euro-code wordt gerekend met een trek-sterkte.Sia 162 [3] en DIN 1045 [4] defini?-ren een ondergrens voor hetwapeningspercentage die in feiteafhankelijk is van de betonsterkte-klasse, omdat die ondergrensdirect wordt gekoppeld aan descheurkracht van de doorsnede.Bij Sia 162 wordt daarbij nog aan-vullend de staafafstand in reke-ning gebracht. Dit toont duidelijkhet verband met de beoogdescheurbeperking: hoe groter destaafafstand, hoe hoger het mini-mum-wapeningspercentage. Sia162 wijst hier ook duidelijk opdoor niet alleen te stellen dat deminimumwapening, zonder devloeigrens te bereiken, debetontrekkracht moet kunnenopnemen die vrijkomt bij scheur-vorming, maar ook de scheurwijd-ten moet begrenzen die optredenbij verhinderde vervormingen. Bijdeze beide voorschriften is geensprake van een relatie met hetmoment in de uiterste grenstoe-stand.In BS 8110 [5] is de relatie met debetonsterkteklasse niet aanwezig:het minimum-wapeningspercen-tage is alleen afhankelijk van debelastingssituatie (trek of buiging)en de vorm van de doorsnede.Uit het voorgaande blijkt dat spra-ke is van een grote verscheiden-heid aan rekenregels. Het voorko-men van bros bezwijken (eenductiliteitscriterium) wordt altijdgenoemd als uitgangspunt, maarhet vertalen van dit criterium ineen concrete rekenregel blijkt toteen grote verscheidenheid aan for-muleringen te leiden, waarbijvooral opvalt dat het aantal varia-belen sterk varieert.Ter illustratie van de invloed vanbijvoorbeeld de hoogte van debetondoorsnede zijn in figuur 2de resultaten van vier simulatiesvan buigproeven weergegeven [6].Het betreft hier balken in hoogtevari?rend van 100 mm tot800 mm, voorzien van 0,125%wapening. Het onderzoek beoog-de het vervormings- en scheurge-drag van een op buiging belaste(on)gewapende rechthoekigebetondoorsnede te beschrijven.Zowel langs de verticale als dehorizontale as is een dimensieloosgemaakte eenheid uitgezet, res-pectievelijk M / Mren / r, waar-in rde kromming is bij hetscheurmoment Mr. Uit de figuuris af te leiden dat, naarmate de lig-ger hoger is, het uiterst opneem-bare moment dichter bij hetscheurmoment ligt. Ook blijkt deductiliteit dan af te nemen, zoalsblijkt uit de na-scheurfase voor deligger met een hoogte van800 mm, die wijst op nagenoegbros bezwijken. Dit in tegenstel-ling tot de liggers met een hoogtevan 100 mm en 200 mm, waarsprake is van een lang vervor-mingstraject bij een nagenoegconstant of zelfs (gering) toene-mend moment.L a m e l l e n m o d e l v o o ro n g e w a p e n d b e t o nAls uitgangspunt bij het modelle-ren is gekozen voor het zoge-noemde lamellenmodel, eenmodel dat recent veelvuldig isgebruikt om via invers modellerende spanning-rekrelatie van betonaf te leiden uit de resultaten vaneen trek- [7] of buigproef [8].Figuur 3 toont de opzet van hetmodel: de doorsnede wordt overde hoogte verdeeld in een aantallamellen. Uit horizontaal even-wicht en momentenevenwichtworden de rek en kromming ineen referentiepunt berekend.In de figuur is aangegeven dat hetna-scheurgedrag van beton wordtbeschreven met een spanning-microscheurwijdterelatie, niet meteen spanning-rekrelatie [7]: na hetontstaan van microscheurvorming3 |Schematische weergavevan het lamellenmodel(a) en modellen gebruiktvoor het beschrijven vanhet gedrag van onge-scheurd en gescheurdbeton (b)4 |Vervormingsgedrag vaneen lamel met micro-scheurvorminga. ontlastend beton bui-ten de microscheurzone(gearceerd energie dievrijkomt)b. geleidelijk toenemenvan de microscheurwijd-te in de scheurzone(gearceerd opgenomenenergie)wwcrwlc (1+ ) + wlamelmicroscheurfct fcta. b.a. b.O n d e r z o e k & t e c h n o l o g i eB erekeningcement 2006 684_+ fctw = wcrelastischsofteningdoorgescheurd21,81,61,41,20,80,60,40,200 1 2 3 4 5 6 7 8 9 101h = 100 mmh = 150 mmh = 250 mmh = 350 mmh = 500 mmh = 800 mm(l/m) 10-3M/Mr(-)M/Mr(-)= 0%materiaalgegevens:Ec= 31 000 N/mm2fct= 2,7 N/mm2Gf;0= 100 N/mmateriaalgegevens:Ec = 31 000 N/mm2fct = 2,7 N/mm2Gf;0 = 100 N/m00.811.21.41.6doorsnedehoogte (mm)schaaleffect van ongewapend beton100 200 300 400 500 600 700 800schaaleffect VBC 1995(volgens de buigtreksterkte-theorie)concentreert de scheurvormingzich in een microscheur (fig. 4a)en de gebieden ter weerszijdenvan deze microscheur ontlastenvia de spanning-rekcurve (fig. 4b).In de berekeningen wordt demicroscheurwijdte omgezet ineen rek door te delen door eenlengte-eenheid. Diverse benade-ringswijzen worden gevolgd. Zokan deze lengte-eenheid bijvoor-beeld constant worden gehoudenvoor alle lamellen en alle belas-tingsstappen [7, 8], of wordengekoppeld aan de microscheur-diepte en deze per belastingsstapen per lamel steeds opnieuw teberekenen [9]. Een uitgebreid the-oretisch onderzoek wees uit dathet de voorkeur verdiende dezelengte-eenheid per belastingsstapopnieuw te berekenen, maar indie betreffende stap dan wel vooralle lamellen dezelfde lengte-een-heid te hanteren. De variabele lcwordt dus per stap berekend uithet krachtenevenwicht. Om toteen oplossing te komen, moesteen additionele randvoorwaardeworden gebruikt. Deze is ontleendaan de uitdrukking voor de scheur-wijdte aan het betonoppervlak vaneen ongewapende doorsnede [10]:w = k1hcr (3)waarin:hcris de scheurdiepte; is de gemiddelde rek in debeschouwde lamel.In het model is k1= 2 aangehou-den en is de uitdrukking toege-past voor de lamel die de grootstepositieve rek (verlenging) onder-gaat.Voor alle lamellen waarin sprakeis van micro-scheurvorming (diezich dus `in de softeningtak vanhet beton bevinden') moet wordenvoldaan aan de voorwaarde dat deenergie die vrijkomt door het ont-spannen van de delen van lamel-len ter weerszijden van de micro-scheur kleiner is dan de energiebenodigd om de microscheur telaten doorgroeien (breukenergie).In figuur 4a-b zijn die bijdragenschematisch weergegeven. Alduswordt getoetst of sprake is van sta-biele scheurvorming, dan wel datongecontroleerde scheurvorming(`snap-back') zal plaatshebben.Zodra de betontrekspanning in deuiterst getrokken lamel is afgeno-men tot nul (w wcr, zie fig. 3 en4) wordt de in de voorgaandebelastingsstap berekende lcvastge-legd en in de volgende belastings-stappen constant gehouden. Descheurwijdte neemt vanaf nu line-air toe met de toename van degemiddelde rek in de lamellenwaarvoor geldt w wcr, de zoge-noemde `doorgescheurde' lamel-len. Deze aanname heeft geeninvloed op het krachtenevenwicht:de betreffende lamellen zijn span-ningsloos geworden.In figuur 5 is schematisch weerge-geven welke gebieden nu zijn teonderscheiden: lineair-elastisch,softening (micro-scheurvorming)en doorgescheurd.Met het model is het gedrag vanongewapende betondoorsnedenonderzocht. Figuur 6a toont hetresultaat als alleen de hoogte vande doorsnede wordt gevarieerd.Overeenkomstig figuur 2 is hetmoment (verticale as) dimensie-loos gemaakt. Uit figuur 6b blijktdat de verhouding tussen MuenMrafhankelijk is van de hoogtevan de ligger. Dit fenomeen ? eenzogenoemd schaaleffect ? is ookbekend uit de VBC-6.1.2, waarinde verhouding tussen de buigtrek-sterkte (volgend uit Mu) en de cen-trische treksterkte (volgend uit Mr)ook afhankelijk is gesteld van dehoogte. Om die reden is in defiguur ook de relatie uit de VBCopgenomen. De theorie blijkt de5 |Betonnen doorsnedeover de hoogte verdeeldin een lineair-elastischgebied, een softening-zone (micro-scheurvor-ming) en een doorge-scheurde zone6 |Met het lamellenmodelgesimuleerd vervor-mingsgedrag van op zui-vere buiging belasteongewapende beton-doorsneden (h = 100 -800 mm) (a) en de hier-uit volgende verhoudingMu/ Mrals functie van deliggerhoogte (b), hetzogenoemde schaaleffectvan op buiging belastbeton (rood); tevens isaangegeven het schaalef-fect van de VBC 1995(blauw)abO n d e r z o e k & t e c h n o l o g i eB erekeningcement 2006 6 85betonstaalongewapend betongewapend beton(l/m) 10-3M/Mr(-)materiaalgegevens:Ec= 31 000 N/mm2fct= 2,7 N/mm2Gf;0= 100 N/m00.20.40.60.811.21.41.61.80 2 4 6 8 10 12 14 16= 0,125 %= 0,08 %= 0,05 %= 0,00 %h = 250 mmtrend van het schaaleffect goed tebeschrijven. Hierbij moet wel wor-den opgemerkt dat de modeluit-komst afhankelijk is van een grootaantal invoerparameters; er issprake van een voor alle beton-soorten `unieke' curve.B e t o n s t a a lDe invloed van mogelijk aanwezigbetonstaal is verwerkt door lamel-len toe te voegen. Deze krijgeneen kracht-vervormingsrelatie dieovereenstemt met die van een sta-len lamel die over de lengte lcdooraanhechting met het beton is ver-bonden [9]. Nadat in het betonscheurvorming is opgetreden, ont-wikkelt zich een aanhechtspan-ning tussen het staal en het beton.Deze wordt constant veronder-steld over de staaflengte. Als eengrenswaarde voor de aanhecht-spanning (voor geribd staal gelijk-gesteld aan b= 2 fctis bereikt,wordt deze constant gehouden enis dan dus onafhankelijk van degrootte van de slip tussen het staalen het beton. Niet alleen de beton-lamellen die direct in verbindingstaan met het betonstaal ondervin-den hiervan invloed: verondersteldis dat de betonlamellen onderlingde `aanhechtkracht' en de mededaardoor veroorzaakte vervormingvan de betonlamellen doorgeven.Uiteraard is hierbij sprake van een`uitdempend' verschijnsel: naar-mate een betonlamel verder ver-wijderd is van een stalen lamelondervindt deze minder invloedvan laatstgenoemde. Deze onder-linge overdracht van de aanhecht-kracht leidt er wel toe dat betonla-mellen aan een additioneletrekkracht worden onderworpen.De ontstane verlengingen van debetonlamellen zorgen er voor datde scheurgroei wordt `geremd';het betonstaal heeft een scheur-wijdte-reducerend effect en zorgter voor dat in de na-scheurfaselanger trekspanningen in hetbeton worden overgedragen (ziefig. 3). Het model geeft dus ookeen verloop van de scheurwijdteover de hoogte van de doorsnede.Dit is schematisch weergeven infiguur 7.De invloed van betonstaal op demomentcapaciteit van een door-snede is getoond in figuur 8. Vooreen doorsnede met een hoogtevan 250 mm zijn de moment-krommingrelaties berekend vooreen hoeveelheid wapening = 0% - 0,125%. De kromming ishier de gemiddelde kromming,dus is niet gelijk aan de krom-ming in de scheur. De doorsnedekan worden belast tot Mu1,35 Mr. De invloed van het softe-ninggedrag van beton komt dantot uitdrukking; het betonstaalheeft dan, mede door de lagewapeningspercentages, nog wei-nig invloed.Bij een verdere toename van dekromming neemt het opneembaremoment af omdat de micro-scheurwijdte toeneemt en debetontrekspanningen dus afne-men. Tegelijkertijd neemt het aan-deel van het betonstaal in dekrachtsopname toe, ook in absolu-te zin zodanig dat vanaf een zeke-re kromming de momentcapaci-teit van de doorsnede weertoeneemt. De doorsnede bezwijktals het betonstaal de rek bij maxi-male belasting (breukrek) bereikt( = 0% - 0,08%) of als de grens-waarde van de betonstuik wordtbereikt ( = 0,125%).In de berekening is uitgegaanvan een betontreksterkte van2,7 N/mm2. Deze relateren aan dekarakteristieke bovengrens van detreksterkte (1,4 fbm) zoals vermeldin de VBC, wijst uit dat de sterkte-klasse dus nagenoeg C12/15 is.Voor deze sterkteklasse geeft deVBC 0min= 0,12%. De moment-krommingrelatie verkregen voor = 0,125% toont dan ook een na-scheurcapaciteit die toeneemt totongeveer M = Mr. Deze capaciteitis in figuur 8 aangeduid als `ducti-liteitsplateau'.In figuur 9 zijn de resultaten voor = 0,125% weergegeven voor debalken, gesimuleerd door Ozboltmet een eindige-elementenmodel[6], en volgens het lamellenmodel.Zowel het breukmoment als devroege na-scheurfase tonen goedeovereenstemming.T e n s l o t t eEen lamellenmodel is opgesteldmet een energiecriterium voor hetberekenen van de scheurvorm ende scheurafstand. De invloed vaneventueel aanwezig betonstaal is7 |Schematische weergavevan de invloed vanbetonstaal op de(micro)scheurwijdte vaneen buigscheur8 |Invloed van het wape-ningspercentage op hetvervormingsgedrag ende ductiliteit van een opzuivere buiging belastedoorsnede (h = 250 mm)O n d e r z o e k & t e c h n o l o g i eB erekeningcement 2006 6862) Onder verantwoordelijkheid van prof.dr.ir. J.C. Walraven en prof.ir. A.C.W.M.Vrouwenvelder.opgenomen. Studies naar het ver-schijnsel buigtreksterkte en na-scheurgedrag hebben uitgewezendat goede overeenstemming metde uitkomsten van experimentenwordt verkregen. Het model isgeschikt voor het uitvoeren vanparameterstudies en voor hetvaststellen van de minimumwa-pening die benodigd is om eengewenste ductiliteit te verkrijgen.Dat laatste vraagt wel om eenduidelijke omschrijving van het-geen met het toepassen van mini-mumwapening wordt beoogd tebereiken. nL i t e r a t u u r1. NEN6720, VoorschriftenBeton, Technische Grondsla-gen voor Bouwconstructies(TGB 1990); Constructieveeisen en rekenmethoden (VBC1995). Nederlands Normalisa-tie-instituut, Delft, 1995.2. Eurocode 2, Design of concre-te structures, Part 1-1: Generalrules and rules for buildings.Final draft prEN 1992-1-1.3. Sia Norm 162, Betonbauten,1989.4. DIN 1045-1, Deutsche NormTragwerke aus Beton, Stahlbe-ton und Spannbeton. 2001.5. BS 8110-1, Structural use ofconcrete. Code of practice fordesign and construction, 1997.6. Ozbolt, J., Ma?stabseffekt undDuktilit?t von Beton- undStahlbetonkonstruktionen.IWB, Universit?t Stuttgart,1995.7. Hordijk, D.A., Local approachto fatigue of concrete. Disser-tatie, TU Delft, 1991.8. Kooiman, A.G., Modellingsteel fibre reinforced concretefor structural design. Disserta-tie, TU Delft, 2000.9. Braam, C.R., Control of crackwidth in deep reinforced con-crete beams. Dissertatie, TUDelft, 1990.10. Beeby, A. W., Concrete in theoceans; Cracking and corrosi-on. Cement and ConcreteAssociation, Technical ReportNo. 1, 1978.11. Keijnemans, J., Minimumwa-pening in gewapend betonnenplaten. Afstudeerrapport TUDelft, 2006.2)9 |Vergelijking tussen uit-komsten van simulatiesmet het model vanOzbolt [6] en met hetlamellenmodelM/Mr(-) 00.20.40.60.811.21.41.61.82h = 100 mmh = 200 mmh = 400 mmh = 800 mm/ - Mr (-) = 0,125 %2,51,50,52100h = 100 mmh = 200 mmh = 400 mm/ - Mr (-)h = 800 mmh = 100 mm - modelh = 200 mm - modelh = 400 mm - modelh = 800 mm - model2 4 6 8 10 12M/Mr(-)