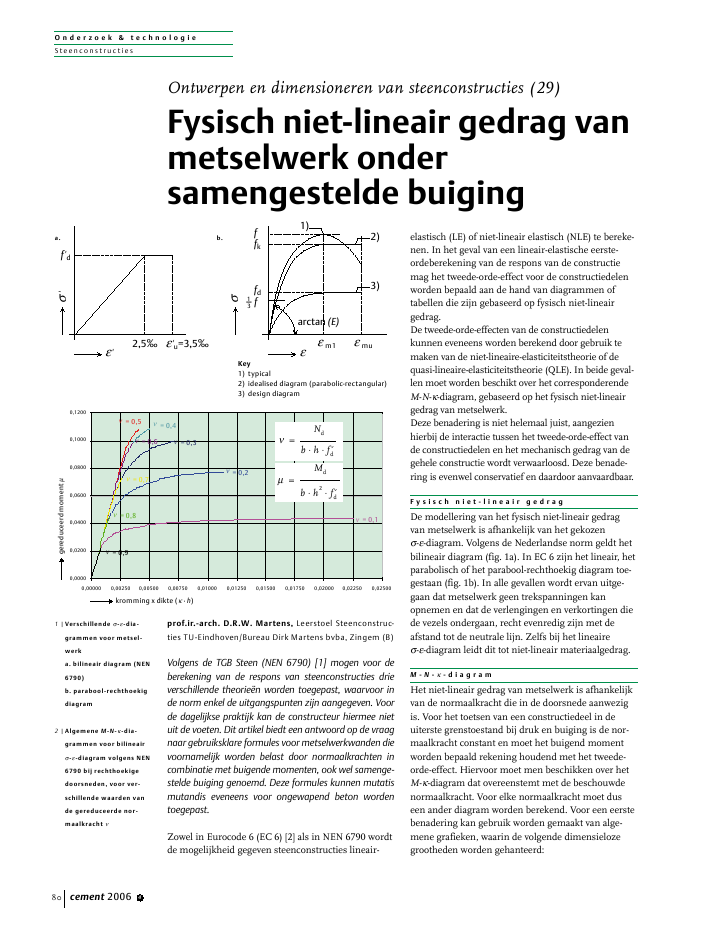
O n d e r z o e k & t e c h n o l o g i eSteencons tr uc tiescement 2006 480prof.ir.-arch. D.R.W. Martens, Leerstoel Steenconstructies TUEindhoven/Bureau Dirk Martens bvba, Zingem (B)Volgens de TGB Steen (NEN 6790) [1] mogen voor deberekening van de respons van steenconstructies drieverschillende theorie?n worden toegepast, waarvoor inde norm enkel de uitgangspunten zijn aangegeven. Voorde dagelijkse praktijk kan de constructeur hiermee nietuit de voeten. Dit artikel biedt een antwoord op de vraagnaar gebruiksklare formules voor metselwerkwanden dievoornamelijk worden belast door normaalkrachten incombinatie met buigende momenten, ook wel samenge-stelde buiging genoemd. Deze formules kunnen mutatismutandis eveneens voor ongewapend beton wordentoegepast.Zowel in Eurocode 6 (EC 6) [2] als in NEN 6790 wordtde mogelijkheid gegeven steenconstructies lineair-elastisch (LE) of niet-lineair elastisch (NLE) te bereke-nen. In het geval van een lineair-elastische eerste-ordeberekening van de respons van de constructiemag het tweede-orde-effect voor de constructiedelenworden bepaald aan de hand van diagrammen oftabellen die zijn gebaseerd op fysisch niet-lineairgedrag.De tweede-orde-effecten van de constructiedelenkunnen eveneens worden berekend door gebruik temaken van de niet-lineaire-elasticiteitstheorie of dequasi-lineaire-elasticiteitstheorie (QLE). In beide geval-len moet worden beschikt over het corresponderendeM-N--diagram, gebaseerd op het fysisch niet-lineairgedrag van metselwerk.Deze benadering is niet helemaal juist, aangezienhierbij de interactie tussen het tweede-orde-effect vande constructiedelen en het mechanisch gedrag van degehele constructie wordt verwaarloosd. Deze benade-ring is evenwel conservatief en daardoor aanvaardbaar.F y s i s c h n i e t - l i n e a i r g e d r a gDe modellering van het fysisch niet-lineair gedragvan metselwerk is afhankelijk van het gekozen--diagram. Volgens de Nederlandse norm geldt hetbilineair diagram (fig. 1a). In EC 6 zijn het lineair, hetparabolisch of het parabool-rechthoekig diagram toe-gestaan (fig. 1b). In alle gevallen wordt ervan uitge-gaan dat metselwerk geen trekspanningen kanopnemen en dat de verlengingen en verkortingen diede vezels ondergaan, recht evenredig zijn met deafstand tot de neutrale lijn. Zelfs bij het lineaire--diagram leidt dit tot niet-lineair materiaalgedrag.M - N - - d i a g r a mHet niet-lineair gedrag van metselwerk is afhankelijkvan de normaalkracht die in de doorsnede aanwezigis. Voor het toetsen van een constructiedeel in deuiterste grenstoestand bij druk en buiging is de nor-maalkracht constant en moet het buigend momentworden bepaald rekening houdend met het tweede-orde-effect. Hiervoor moet men beschikken over hetM--diagram dat overeenstemt met de beschouwdenormaalkracht. Voor elke normaalkracht moet duseen ander diagram worden berekend. Voor een eerstebenadering kan gebruik worden gemaakt van alge-mene grafieken, waarin de volgende dimensielozegrootheden worden gehanteerd:Ontwerpen en dimensioneren van steenconstructies (29)Fysisch niet-lineair gedrag vanmetselwerk ondersamengestelde buiging1 |Verschillende --dia-grammen voor metsel-werka. bilineair diagram (NEN6790)b. parabool-rechthoekigdiagram2 |Algemene M-N--dia-grammen voor bilineair--diagram volgens NEN6790 bij rechthoekigedoorsneden, voor ver-schillende waarden vande gereduceerde nor-maalkracht m1 muf'd0,8 MuMuMffkfd1f3_'u=3,5 0,8Mu u2,5 ''arctan (E)arctg (EI)d1)NLEQLEKey1) typical2) idealised diagram (parabolic-rectangular)3) design diagram2)3)0,00000,02000,04000,06000,08000,10000,12000,00000 0,00250 0,00500 0,00750 0,01000 0,01250 0,01500 0,01750 0,02000 0,02250 0,02500 = 0,1 = 0,2 = 0,3 = 0,5 = 0,4 = 0,6 = 0,7 = 0,8 = 0,9gereduceerdmomentkromming x dikte ( ? h)??Mdb h2f?d =Ndb h f?d =a. b.O n d e r z o e k & t e c h n o l o g i eSteencons tr uc tiescement 2006 4 81gereduceerd moment:?Mdb h2f?d =Ndb h f?d =Nl r+2bh=Mr l?2bhh2h3? bh212r l?( )= =r l?h=Emetf?d0 0025,=Mbh212E r l?( )=eh6: ?E12 f?d h of ? h0 03,= =gereduceerde normaalkracht:(benuttingsgraad )?Mdb h2f?d =Ndb h f?d =Nl r+2bh=Mr l?2bhh2h3? bh212r l?( )= =r l?h=Emetf?d0 0025,=Mbh212E r l?( )=eh6: ?E12 f?d h of ? h0 03,= =relatieve kromming: hIn figuur 2 is een dergelijke grafiek getekend metwaarden van vari?rend van 0,1 tot 0,9 voor rechthoe-kige doorsneden met breedte b en hoogte h conformNEN 6790. Hierbij is f?dde rekenwaarde van de met-selwerkdruksterkte.Voor exacte berekeningen kan een specifieke grafiekworden berekend voor de juiste waarde van N.Volgens de meest recente versie van NEN 6790 (2005)mag het M-N--diagram ook worden benaderd dooreen vereenvoudigd bilineair diagram zoals weergege-ven in figuur 3. De aandachtige lezer zal opmerkendat dit diagram afwijkt van het (onrealistische)diagram dat in de oude versie van de TGB Steen wasopgenomen.A l g e m e n e w e r k w i j z eDe gedetailleerde berekening van het M-N--diagramvoor een specifieke waarde van de normaalkrachtmoet gebeuren aan de hand van de evenwichtsverge-lijkingen, de compatibiliteitsvergelijkingen en de con-stitutieve relaties. Hierbij moet onderscheid wordengemaakt tussen gescheurde en ongescheurde door-sneden. Voor --diagrammen met een plastische takmoet bovendien worden ge?valueerd of de rekken inde doorsnede al dan niet kleiner zijn dan de maxi-male elastische rek e. Voor het bilineaire en het para-bool-rechthoekige --diagram is de maximale elasti-sche rek respectievelijk 2,5o/ooen 2,0o/oo(fig. 1).L i n e a i r - e l a s t i s c h g e d r a gVoor vrij brosse materialen zoals metselwerk metgeperforeerde baksteen, kan het aangewezen zijn eenlineair-elastisch gedrag aan te nemen. In dit geval kanhet M-N--diagram worden berekend zoals in figuur4 is aangegeven.Als de excentriciteit e h/6, is de doorsnede onge-scheurd en kan de M--relatie als volgt worden bere-kend.Evenwichtsvoorwaarden(1)?Mdb h2f?d =Ndb h f?d =Nl r+2bh=Mr l?2bhh2h3? bh212r l?( )= =(2)Formule a1Formule a2Formule1Formule2Formule3Formule a3Formule6Formule7?Mdb h2f?d =Ndb h f?d =Nl r+2bh=Mr l?2bhh2h3? bh212r l?( )= =r l?h=Emetf?d0 0025,=Mbh212E r l?( )=0 eh6: ? E12 f?d h of ? h0 03,= =Compatibiliteitsvoorwaarde(3)Formule a1Formule a2Formule1Formule2Formule3Formule a3Formule6Formule7?Mdb h2f?d =Ndb h f?d =Nl r+2bh=Mr l?2bhh2h3? bh212r l?( )= =r l?h=Emetf?d0 0025,=Mbh212E r l?( )=0 eh6: ? E12 f?d h of ? h0 03,= =Constitutieve relatiesl= El(4)r= Er(5)Formule a1Formule a2Formule1Formule2Formule3Formule a3Formule6Formule7?Mdb h2f?d =Ndb h f?d =Nl r+2bh=Mr l?2bhh2h3? bh212r l?( )= =r l?h=Emetf?d0 0025,=Mbh212E r l?( )=0 eh6: ? E12 f?d h of ? h0 03,= =Rekening houdend met (4) en (5) kan vergelijking (2)worden omgevormd tot(6)Formule a1Formule a2Formule1Formule2Formule3Formule a3Formule6Formule7?Mdb h2f?d =Ndb h f?d =Nl r+2bh=Mr l?2bhh2h3? bh212r l?( )= =r l?h=Emetf?d0 0025,=Mbh212E r l?( )=0 eh6: ? E12 f?d h of ? h0 03,= =Eliminatie van ren luit (6) en (3) levert uiteindelijkde gezochte M--relatie, of in dimensieloze vorm:(7)Formule a1Formule a2Formule1Formule2Formule3Formule a3Formule6Formule7?Mdb h2f?d =Ndb h f?d =Nl r+2bh=Mr l?2bhh2h3? bh212r l?( )= =r l?h=Emetf?d0 0025,=Mbh212E r l?( )=0 eh6: ? E12 f?d h of ? h0 03,= =Als de excentriciteit e > h/6, is de doorsnedegescheurd en moet de M--relatie als volgt wordenberekend.3 |Niet-lineair-elastisch(NLE) en quasi-lineair-elastisch (QLE) M-N--diagram4 |Spannings- en vervor-mingsdiagrammen bijlineair-elastisch gedraga. ongescheurde door-snede (e h/6)b. gescheurde doorsnede(e > h/6)0,8 MuMuM 0,8Mu uarctg (EI)dNLEQLEbbbaaaada bdxO n d e r z o e k & t e c h n o l o g i eSteencons tr uc tiescement 2006 482Evenwichtsvoorwaarden(8)Nbxr2=M Nh2x3? =rx=x2hf?dE=h6eh2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =(9)101213141516Nbxr2=M Nh2x3? =rx=x2hf?dE=h6eh2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =Compatibiliteitsvoorwaarde(10)Nbxr2=M Nh2x3? =rx=x2hf?dE=h6eh2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =Constitutieve relatiesr= Er(11)Uit de vergelijkingen (8), (10) en (11) kan de hoogtevan de gedrukte zone x worden berekend:(12)023456Nbxr2=M Nh2x3? =rx=x2hf?dE=h6eh2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =Eliminatie van x uit (9) en (12) levert dan de gezochteM--relatie, of in dimensieloze vorm:Formule8Formule9Formule 10Formule 12Formule 13Formule 14Formule 15Formule 16Nbxr2=M Nh2x3? =rx=x2hf?dE=h6eh2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =(13)Nbxr2=M Nh2x3? =rx=x2hf?dE=h2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =Deze formules kunnen gemakkelijk in een rekenbladworden verwerkt. In figuur 5 zijn de resultaten weer-geven van de berekening van het M-N--diagram vaneen rechthoekige doorsnede bij lineair-elastisch--diagram.M - N - v o l g e n s N E N 6 7 9 0Volgens de Nederlandse metselwerknorm moet voorde berekening van het M-N--diagram het bilineair--diagram worden gebruikt. Voor een dergelijkdiagram is de berekening iets bewerkelijker. Na enigeenvoudig rekenwerk kunnen de volgende M--rela-ties worden bepaald.0 r 2,5o/ooen l 0:(14)Formule 13Formule 14Formule 15Formule 16h6eh2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =2,5o/oo r 3,5o/ooen l 0:(15)Formule 14Formule 15Formule 16h6eh2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =0 r 2,5o/ooen l< 0:(16)Formule 14Formule 15Formule 16h6eh2: ? 0 529 f?dE h ?, of ? 0 51800 h ?, = =? h0 03,=?1 ?211 ?450 h ? =? 0 5,1800 h ? =2,5o/oo r 3,5o/ooen l< 0:Formule 17Formule 18Formule 19Formule a4Formule 20Formule 21Formule 22?121800 h + 1 ?1800 h ? 11600 h 1 2?? =0 643 1: ?u<