Constructie & uitvoering Detaillering ir. E.L.M.G. van den Brande, BAM Advies & Engineering ing. N.T. Loonen (co-auteur), ABT BV, Velp/ Delft/ Ant- werpen Aan de hand van een praktijkvoorbeeld wordt de wape- ning berekend in een funderingsplaat, belast door zware kolomlasten. Er wordt geen ontwerpberekening maar eerder een controleberekening uitgevoerd van een be- staande keldervloer met opgegeven dimensies en belas- tingen. De berekening van de wapening is uitgevoerd met het computerprogramma Esa Prima Win. Dit program- ma maakt het mogelijk om de berekende inwendige krachten om te zetten naar de benodigde wapening. Praktijkvoorbeeld Uit een keldervloer wordt een repeterende strook gelicht. In deze strook wordt de wapening berekend die doorgezet kan worden voor de gehele funde- ringsvloer (fig. 1). Gegevens: ? funderingsplaat: 5,0 x 22,0x 0,65m 3(bx l x d) ? kolommen: 400x 590 mm 2, oplegplaat (fig. 2) 500 x 690 mm 2 ? palen: Ø450 mm ? sterkteklasse keldervloer: B 35 ? sterkteklasse palen: B 25 ? staalsoort: FeB 500 ? wapeningspercentage: # Ø12?100 leidt tot A s= 1130 mm 2/m ?E -modulus beton B 35 gescheurd: E f= 2800 + 6100 ?0
4300(zie tabel 15 NEN 6720) E f= 2800 + 6100 ?0,17= 3860 N/ m m 2< 4300 E f= 4300 N/ m m 2 Randvoorwaarden Palen De funderingsplaat rust op de palen. Uitgangspunt is dat de palen geen momenten kunnen overdragen. De oplegging is gemodelleerd als een scharnierende puntvormige verende ondersteuning. De veerconstante van de palen kan bepaald worden uit het sonderingsrapport. Hierin wordt bij een be- paalde belasting de zetting gegeven waarmee de veer- stijfheid van de paal in de grond berekend kan worden. In de ontwerpfase kan de veerstijfheid van de paal be- rekend worden met een benaderingsformule. De veerconstante van de paal wordt bepaald met de formule De factor 2 in de noemer wordt geïntroduceerd om de zettingen onder de paalpunt in rekening te brengen. De paal wordt op centrische druk belast, waardoor het beton ongescheurd is. Volgens de NEN6743 mag de elasticiteitsmodulus van de paal ge- lijkgesteld worden aan 20 000 N/mm 2. Ep= 20 000N/ m m 2 lp= 10 000mm Randen De plaatranden in lengterichting zijn voorzien van symmetrierandvoorwaarden. Hierbij wordt de ver- draaiing om de lengteas van de rand verhinderd. k 20000 159043 ? 2 10000 ? 159043 N/m m == Ap ? 450 2 4 ? 159043mm == 2 k E pAp ? 2 l p? = ?0 1130 ? 100 1000 650 ? 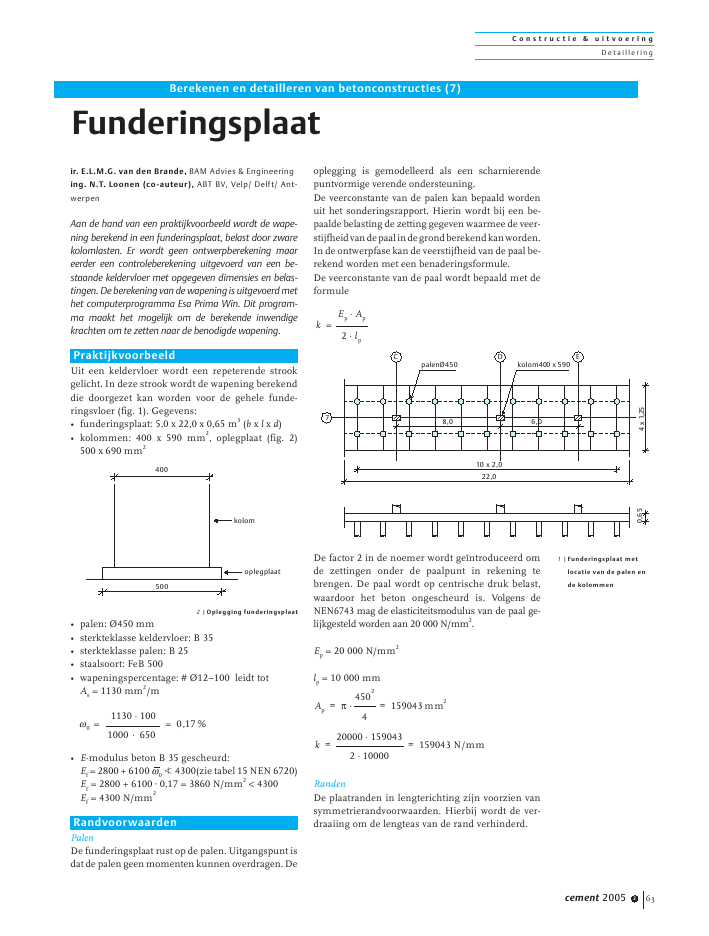017 %, = = Funderingsplaat Berekenen en detailleren van betonconstructies (7) 1 |Funderingsplaat met locatie van de palen en de kolommen C 7 D E palen 450 Ø 22,0kolom400 x 590 10x2,0 4x1,25 0,65 8,0 6,0 cement 2005 3 63 400 500 kolom oplegplaat 2 |Oplegging funderingsplaat Constructie & uitvoering Detaillering cement 2005 3 64 Belastingen Het eigen gewicht van de funderingsplaat wordt door het programma gegenereerd (0,65 ?24= 15,6 kN/m 2). De gelijkmatig verdeelde veranderlijke belasting be- draagt: Q rep = 40 kN/m 2. Uitgangspunt is dat de be- lasting zich over het gehele oppervlak gelijkmatig ver- deelt. Er zijn geen belaste en onbelaste velden. Kolomlasten locatie PB (kN) VB (kN) BC (kN) Q BC(kN/m 2) C 7 800 545 1777 5151 D 7 1007 700 2258 6544 E 7 568 497 1427 4136 PB = permanente belasting VB = veranderlijke belasting BC (kolomlast) = 1,2 ?PB + 1,5 ?VB Q BC = BC / oppervlak oplegplaat (500 x 690) Belastingscombinaties Fundamentele combinatie (UGT ? uiterste grens- toestand) 1,2 ?(EG vloer + PB kolommen ) + 1,5 ?(VB vloer + VB kolommen ) 1,35 ?(EG vloer + PB kolommen ) Incidentele combinatie (BGT) (EG vloer + PB kolommen ) + (VB vloer + VB kolommen ) (EG vloer + PB kolommen ) Wapeningsberekening met het programma Esa Prima Win De berekening is een lineair-elastische berekening. Met het eindige-elementenprogramma worden de inwendige spanningen in de plaatelementen bere- kend. Met deze spanningen worden de inwendige krachten en momenten bepaald. Om de plaat te kunnen wapenen zijn wapenings- grootheden of wapeningskrachten en -momenten benodigd. Deze wapeningsgrootheden M x, M y, N xen N yworden berekend uit de inwendige krachten en momenten m x, m y, m xy, nx, nyen q xy. M x= m x+ of - m xy My= m y + of - m xy Nx= n x+ ?q xy? N y= n y+ ?q xy? Na het invoeren van de dekking en de staafdiame- ters (om de inwendige hefboomsarm te bepalen) be- rekent het computerprogramma met behulp van de wapeningsgrootheden de benodigde wapening in de opgegeven wapeningsrichting. Zowel de boven- als de onderwapening worden opgegeven in mm 2/m. Na het berekenen van de theoretische wapening wordt de scheurwijdtecontrole volgens NEN6720 uit- gevoerd. De figuren 4 t.m. 7geven de berekende wapening in zowel de boven- als onderlaag voor beide wapenings- richtingen. Wapening in de doorsnede Met de resultaten uit de eindige-elementenbereke- ning kan de wapening getekend worden. De mini- mumwapening in de doorsnede voor sterkteklasse B 35 bedraagt 0,18%. De toe te passen wapening hoeft echter niet meer te zijn dan 1 ,25 maal de berekende wapening. Als ba- siswapening wordt zowel voor de boven- als de onder- wapening een net toegepast: # Ø 12-150 (= 754 mm 2). De kleurpatronen geven de hoeveelheid benodigde wapening oplopend van 0 naar de maximaal beno- digde hoeveelheid mm 2/m zoals vermeld in de schaalverdeling. Door de ondergrens in de schaalverdeling te wijzi- gen verkrijgt men een beeld, waar en hoeveel bij- A = 0,18 ? smin ; 1000 650 ? 100 1170 = mm /m 2 kolomlast Q BC -5151.0 GZ kolomlast Q BC -6544.0 GZ kolomlast Q BC -4136.0 GZ hoekverdraaiing verhinderd 3 |Eindige-elementenmodel met belastingen en rand- voorwaarden 4 |Benodigde onderwape- ning in de X-richting voor de eerste laag 5 |Benodigde onderwape- ning in de Y-richting voor de tweede laag 520 480 440 400 360 320 280 240 200 160 120 80 400 (mm2/m) 6 |Benodigde bovenwape- ning in de X-richting voor de eerste laag 7 |Benodigde bovenwape- ning in de Y-richting voor de tweede laag 1820 1680 1540 1400 1260 1120 980 840 700 560 420 280 140 0 (mm 2/m) hoekverdraaiing verhinderd Constructie & uitvoering Detaillering cement 2005 3 65 legwapening bovenop het basisnet geplaatst moet worden (fig. 8). De minimaal benodigde wapening bedraagt 1,25 x de berekende wapening. De ondergrens in de schaalverdeling wordt het toe te passen basisnet : 1,25 = 754 : 1,25 = 603 mm 2/m. In de blauwe zone is er voldoende wapening aanwezig aangezien hier de maximaal berekende wapening 603mm 2/m bedraagt, terwijl er 754 mm 2/m is toegepast. Binnen de gekleurde zone moet wapening worden toegevoegd. In figuur 8 is enkel de bijlegwapening bepaald voor de onderwa- pening in de X-richting. Voor de onderwapening in de Y-richting moet het proces worden herhaald. Uit figuur 8blijkt dat de maximale onderwapening in de X-richting onder de kolom 1750mm 2/m moet bedragen. De piekwaarde wordt verdeeld over een bredere zone. In figuur 9wordt de spreiding van de piekwaarden gegeven. De breedte van de zone waarin bijlegwapening nood- zakelijk is, bedraagt 3300 mm. De spreidingsbreedte van de kolom tot de onderwa- pening bedraagt: 500+ 2 ?598 = 1696 mm. Met behulp van de spreiding van de piekwaarden uit figuur 9 wordt de gemiddelde wapening bere- kend in de zone 1696 mm. De benodigde wapening op de rand van de 1696mm zone bedraagt 1088 mm 2/m. Het vlakje (breedte 0,30 m) met de piekwaarde 1750mm 2/m wordt volledig in reke- ning gebracht. Voor de zone tussen de piekwaarde en de rand van de 1696 mm zone wordt het gemid- delde genomen. De benodigde wapening per meter in de zone van 1696 mm wordt: Tussen de randen van de zones 1696 mm en 3300mm moet ook nog wapening worden toegevoegd. Dit wordt het gemiddelde van 603 mm 2/m en 1088mm 2/m = (603 + 1088) : 2 = 846 mm 2/m. Deze waarde is kleiner dan de minimumwapening. De benodigde wapening in deze zone wordt daarom 1,25 ?846= 1058 mm 2/m. Er wordt voor gekozen om onder de kolom in de zone 1700 mm staven # Ø12-150 bij te leggen. De totale wapening bedraagt in dit gebied (fig. 10): Ø12-150 + Ø12-150 = 754 + 754 = 1508 mm 2/m (> 1456 mm 2/m). Tussen de randen van de zones 1700 mm en 3300mm wordt Ø12- 300bijgelegd. In deze zone bedraagt de tota- le wapening 754+ 376 = 1130 mm 2/m (> 1058 mm 2/m). Ook de staaflengte kan worden berekend aan de hand van figuur 9. Volgens figuur 9 bedraagt de berekende staaflengte 1580mm. Deze waarde moet worden ver- hoogd met de verankeringslengte en met 2d om de verschoven momentenlijn in rekening te brengen. De verankeringslengte wordt: l vo = basisverankeringslengte \b1 040 1 01 35 12 ? ,? ?? \f? ?? 0 = 28 , ,= \b1 040 1 01 c ?k - ---- ? ,? ?? \f? ?? 024 voor geribd staal , < ,= lvo \b1?k fs fb? ?? = 2 1456 mm /m 2 = Asgem; 300 ? 1750 + (1696 ? 300) ? 1750 1088 + 2 1696 = 8|Benodigde bijlegwape- ning voor de onderwape- ning in X-richting mm /m 2 1696 3300 d = 650 - 40 - 12 = 598 mm 690 mm 1886 300 603 mm /m 2 1750 mm /m 2 1088 1580 Bijlegwapening t.p.v kolommen A = 12 Ø12-150 l = 3500 mm Bijlegwapening in X-richting Bijlegwapening in Y-richting B A B B A B 3300 3300 4 x 1250 B = 3 Ø12-300 l = 3500 mm Ø 12-150 Ø 12-150 C D E 7 10 | Gewapende funderings- plaat (mm2/m) 1820 1726 1633 1539 1446 1352 1258 1165 1071 977 884 790 697 603 9 |Spreiding van de piek- waarden Constructie & uitvoering Detaillering cement 2005 3 66 De gereduceerde verankeringslengte wordt: De totale benodigde lengte van de staaf bedraagt nu: 1580+ 2 ?598 + 2 ?316 = 3408 mm. De gekozen staaflengte wordt 3500 mm (= handels- lengte wapeningsstaaf : 4). In de Y-richting wordt dezelfde wapening aangehou- den als in de X-richting. De berekening is hier buiten beschouwing gelaten. Uit de figuren 6 en 7volgt dat de berekende boven- wapening onder de 520 mm 2/m blijft. De benodig- de minimumwapening bedraagt 1,25 ?520 = 650 mm 2/m. De aanwezige wapening van het basis- net 754 mm 2/m is voldoende, zodat hier geen bij- legwapening nodig is. Met de gekozen wapening moet de stijfheid van de plaat opnieuw worden berekend. Hiermee wordt opnieuw de wapening bepaald. Deze herberekening wordt hier buiten beschouwing gelaten. Pons Zowel bij de kolommen als bij de palen wordt de fun- deringsplaat gecontroleerd op pons. Uit de bereke- ning volgt de maximale reactiekracht van de palen in de UGT: 835 kN. Vaak wordt in de praktijk de ponsberekening uitge- voerd voor een paalbelasting die gelijk is aan de ca- paciteit van de paal. De capaciteit van de paal is de kleinste waarde van de geotechnische en de beton- technische capaciteit. In dit praktijkvoorbeeld be- draagt de maximale paalcapaciteit 1500kN. De funderingsplaat wordt gecontroleerd op de op- tredende kolombelasting. De maximale kolomlast in de UGT bedraagt: 2258 kN. De ponscontrole kan nu worden uitgevoerd voor palen en kolommen. Toetsingscriterium: ?d??u Berekening van de uiterst opneembare schuifspan- ning zonder ponswapening f b= 1,4 N/ m m 2(beton B 35) d = 650 - 40- 12= 598 mm k d= 1,5 - 0,6d= 1,5 - 0,6 ?0,598 = 1,14 Toegepaste wapening boven de paal: Ø12-150. ?0= 754 ?100/ (1000 ?650) = 0,12 % Toegepaste wapening onder de kolom: Ø12-75. ?0= 1508 ?100 / (1000 ?650) = 0,23% Voor zowel de kolom als de palen geldt: ?1= 1,12 N/ m m 2 f ?b= 21 N/ m m 2(beton B 35) ?2= 0,15 ?21= 3,15 N/ m m 2 ?s= 0N/ m m 2(geen ponswapening) ?u= 1,12 + 0= 1,12 N/ m m 2 Rekenwaarde voor de schuifspanning: perimeter p = ? ?(d+ a) Paal: F d= 1500 kN a = 450 mm p = ? ?(598 + 450) = 3292 mm ?d ? ?uGeen ponswapening noodzakelijk Kolom: F d= 2258 kN a = 2 / ? ?(al+ a b) a = 2 / ? ?(690 + 500) = 758 mm p = ? ?(598 + 758) = 4258 mm ?d ? ?uGeen ponswapening noodzakelijk Voor de tweede periferie is geen ponscontrole nood- zakelijk. Conclusie Het berekenen van de wapening met behulp van een computerprogramma kan veel tijd besparen. In het bijzonder wanneer de plaat een willekeurige vorm heeft of wanneer de belastingen en opleggingen wil- lekeurig op de plaat aangrijpen. Wel moet de con- structeur erop letten dat hij de resultaten kritisch on- derzoekt. Het is altijd aan te raden om eveneens een globale handberekening te maken. De resultaten mogen niet te veel afwijken van de berekende resul- taten uit het computerprogramma. ? ?d 2258 10 3 ? 4258 598 ? 0 N/mm 1 N/mm,12 < ,89 == 22 ?d 1500 10 3 ? 3292 598 ? 0 N/mm 2 112 N/mm, < ,76 == 2 ?d p ? d = Fd ?2 015 , f? b 5 N/mm 2  ? = ?1 0,8 ? 1,4 ? 1,14 ? 3  = 0,23 = 0,78 1,12 N/mm 2 ?1 0,8 ? 1,4 ? 1,14 ? 3  = 0,12 = 0,62 1,12 N/mm 2 ?1 08, f bkd ?0 3 08 , f b?  ?? ? = ?u ?1 ?s + ?2  = lvr lvo As;benodigd As;aanwezig ? 3231476 1508 ? 316 mm === lvo 028 , 12435 21 ?? 323 mm ==