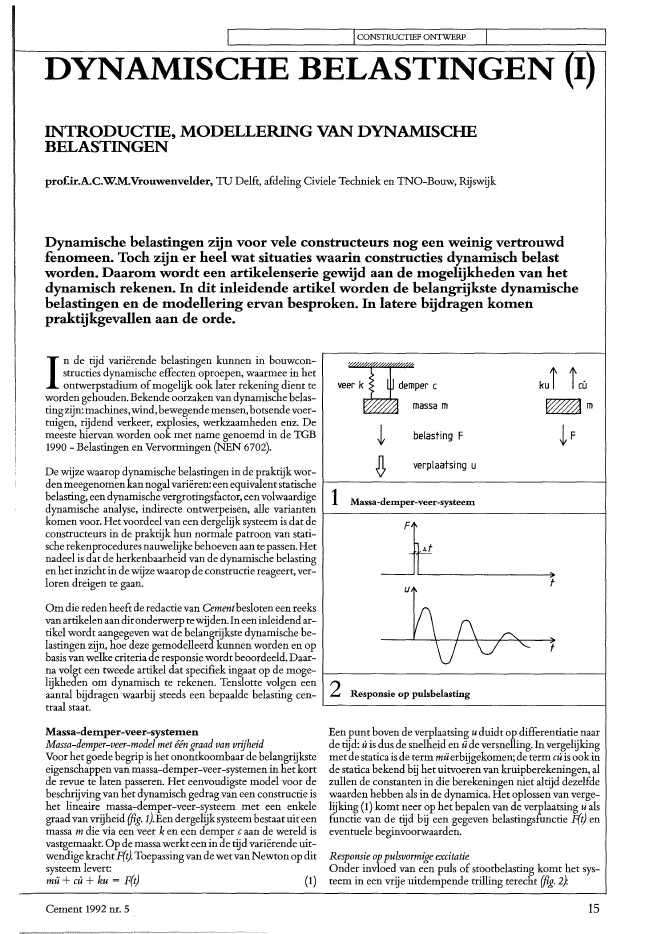
I ICONSTRUCTIEF ONTWERP I IDYNAMISCHE BELASTINGEN ~I), ~INTRODUCTIE, MODELLERING VAN DYNAMISCHEBELASTINGENprof.ir.A.C.W.M.Vrouwenvelder. TU Delft, afdeling Civiele Techniek en TNO-Bouw, RijswijkDynamische belastingen zijn voor vele constructeurs nog een weinig vertrouwdfenomeen. Toch zijn er heel wat situaties waarin constructies dynamisch belastworden. Daarom wordt een artikelenserie gewijd aan de mogelijkheden van hetdynamisch rekenen. In dit inleidende artikel worden de belangrijkste dynamischebelastingen en de modellering ervan besproken. In latere bijdragen komenpraktijkgevallen aan de orde.Inde tijd vari?rende belastingen kunnen in bouwcon-structies dynamische effecten oproepen, waarmee in hetontwerpstadium ofmogelijk ook later rekening dient teworden gehouden. Bekende oorzaken van dynamische belas-tingzijn: machines,wind,bewegende mensen,botsendevoer-tuigen, rijdend verkeer, explosies, werkzaamheden enz. Demeeste hiervan worden ook met name genoemd in de TGB1990 - Belastingen en Vervormingen (NEN 6702).De wijze waarop dynamische belastingen in de praktijk wor-ve~perc- .----massa mt belasting F~ verplaatsing ukU? ?c?den meegenomen kan nogalvari?ren: een equivalentstatische f - - - - - - - - - - - - - - - - - - - - - - - - 1belasting, een dynamische vergrotingsfactor, eenvolwaardige 1 Massa-demper-veer-systeemdynamische analyse, indirecte ontwerpeisen, alle varianten f - - - - - - - - - - - - - - - - - - - - - - - - - - Ikomen voor. Het voordeel van een dergelijk systeem is dat deconstructeurs in de praktijk hun normale patroon van stati-sche rekenprocedures nauwelijke behoeven aan tepassen. Hetnadeel is dat de herkenbaarheid van de dynamische belastingen het inzichtin de wijze waarop de constructie reageert, ver-loren dreigen te gaan.Omdie reden heeft de redactie van Cementbesloten een reeksvanartikelenaanditonderwerp tewijden. Ineeninleidend ar-tikel wordt aangegeven wat de belangrijkste dynamische be-lastingen zijn, hoe deze gemodelleerd kunnen worden en opbasis van welke criteria de responsie wordt beoordeeld. Daar-na volgt een tweede artikel dat specifiek ingaat op de moge-lijkheden om dynamisch te rekenen. Tenslotte volgen eenaantal bijdragen waarbij steeds een bepaalde belasting cen-J_f_~)uff2 Responsie op pulsbelastingtraal staat. ' - - - - - - - - - - - - - - - - - - - - - - - - - - 1Massa-demper-veer-systemenMassa-demper-veer-model met ??ngraad van vrijheidVoor het goede begrip is het onontkoombaar de belangrijksteeigenschappen van massa-demper-veer-systemen in het kortde revue te laten passeren. Het eenvoudigste model voor debeschrijving van het dynamisch gedrag van een constructie ishet lineaire massa-demper-veer-systeem met een enkelegraad vanvrijheid (fig. 1).Een dergelijk systeem bestaat uit eenmassa m die via een veer k en een demper caan de wereld isvastgemaakt. Op de massawerkt een in de tijd vari?rende uit-wendige kracht F(t).Toepassingvan de wetvanNewton op ditsysteem levert:m? + cu + ku = F(t} (1)Cement 1992 nr. 5Een punt boven de verplaatsing u duidt op differentiatie naarde tijd: uis dus de snelheid en ? de versnelling. Invergelijkingmetde staticais de term m?erbijgekomen;de term cuis ookinde statica bekend bij het uitvoeren van kruipberekeningen, alzullen de constanten in die berekeningen niet altijd dezelfdewaarden hebben als in de dynamica. Het oplossen van verge-lijking (1) komt neer op het bepalen van de verplaatsing u alsfunctie van de tijd bij een gegeven belastingsfunctie F(t) eneventuele beginvoorwaarden.Responsie oppulsvormige excitatieOnder invloed van een puls ofstootbelasting komt het sys-teem in een vrije uitdempende trilling terecht (fig. 2).15ICONSTRUCTIEF ONTWERPu = Uoexp (- We ~t) sin (we t J1- ?; )- Uoexp (- We ~t) sin (wet) (2)Hierin is We = [fTm de eigenfrequentie van het (ongedempte)systeemen ~ = c/2 jfmde relatieve demping.Vergelijking (2)is eenvoudig te verifi?ren door substitutie ervan in (1). Dewaarde van Uovolgt uit het toepassen van de wet van Newtonop hetkorte interval Lltdatde stootwerkt. Direct na de stoot isde snelheid ?(O) = SofmmetSo = FLlt,dewaardevandestoot.Uit (2) volgt verder dat ?(O) = WeUO' waarmee gevondenwordt: Uo = Sofmwo' De benadering achter het == teken in (2)geldt alleen bij lichtgedempte systemen (~< < 1).De meestecivieltechnische constructies kunnen tot deze categorie wor-den gerekend.De demping ~ligtmeestalindeordevan 1?2%.Opgemerkt wordt verder dat systemen met meer graden vanvrijheid (n-massa-veer-systeem) ook meer eigenfiequentiesbezitten. Het gaat te ver dit nader uit te werken.Responsie op harmonische belastingBij een harmonische belasting F = Fosin(wt) is de responsieeveneens harmonisch en wel met dezelfde frequentie w, maarten opzichte van de belasting verschoven in fase:u = uosin(wt - cp) (3)Vergelijking (3) is de stationaire oplossing waarbij eventueleinstelverschijnselen geacht worden te zijn uitgedempt. Dewaarde van Uovolgt door invulling in (1).In figuur 3is voor de harmonische belasting de verhouding H= uofFo uitgezetals functie van de frequentie vandebelasting.Uiteen dergelijke figuur valtveel te leren over het dynamischgedrag van een constructie. Voor lage frequenties reageert hetsysteemquasi-statisch: H(00) = 11k.Bij frequenties inde buurtvan de eigenfrequentie treedt opslingering op. De maximaleopslingeringwordt door de dempingbepaald: H(we) = 1I2k~.Bij zeer grote frequenties gaan de belastingsfluctuaties te snelen komt het systeem uiteindelijkhelemaal niet meer in bewe-ging: H(00) = o.12'?k -IIIIII1_ Ik I;-----r----~==--~,We W3 Responsie op harmonische belasting-~ I\A- V'\TV\ }4 Belasting als som van sinussen, model voor stationairebelastingn+ _---'--0'----__+ ________~[]_L_____________Responsie op willekeurige belasting rt-,Voor de bepaling van de responsie op een willekeurige belas- I ~ting bestaan er in principe twee strategie?n: de berekening in ~---~=~==~~=~========-------1het frequentiedomein en de berekening in het tijdsdomein.By de berekening inhet frequentiedomeinwordtde belastingF(t) geschematiseerd als een som van harmonische functies,zoals aangegeveninfiguur 4. Deresponsievooriedere harmo-nische belastingwordt afzonderlijk berekend; daarnawordenalle resultaten gesommeerd.In het tijdsdomeinwordt de belasting F(t)geschematiseerd alseen reeks van pulsen ofkortstondige belastingsblokken in detijd, zoals aangegeven in figuur 5. Vervolgens wordt de res-ponsievan ieder blok afzonderlijkberekend enworden de re-sultatengesommeerd. Een alternatiefis dat steeds de snelheiden verplaatsing aan het einde van een blok worden berekend;die worden beschouwd als beginvoorwaarden voor het vol-gende blok. Zo kan, beginnend bij het eerste blok, de geheletijdas worden doorgerekend. Met name voor systemen metmeer graden van vrijheid is dit alternatiefbeter uitvoerbaar;de methode doet bovendien geen beroep op het superpo-sitiebeginsel en kan daarom ook worden gebruikt voor niet-lineaire systemen.welke methode in een bepaald geval wordt gekozen hangt165 Belasting als som van pulsen, model voor transientbelastingvan de omstandigheden af Meestal wordt een frequentie-domein-analyse voor langdurige belastingen gebruikt en eentijdsdomein-analyse voor kortstondige.Modellering van belastingenFiguur 6 geeft een mogelijke indeling van belastingen in ver-schillende categorie?n. Hierna wordt van elke categorie eenkorte bespreking gegeven en worden voorbeelden uit de con-structiepraktijk genoemd. Op enkeledaarv;lllwordtindever-volgartikelen nog dieper ingegaan. Voor de goede orde: erwordt steeds gesproken over een kracht, maar de modellenzijn even goed bruikbaarvoor opgedrongen verplaatsingen ofvoor de onderliggende processen in het krachtmodel zoalswindsnelheid, golfhoogte enz.Deterministische modellenHarmonische belastingDe harmonische belasting wordt gegeven door:F = Fosin(wt) (4)Cement 1992 nr. 5I harmonischr-- periodiek- deterministisch ~Ltransientbelasting _ puls-Estationair- stochastisch blokkentransient6 Indeling dynamische belastingenr-------------------------------------------~II----'F/'\ /'\ /'\ 4VV \:I\J -3rr Focos (3wtl7 Benadering blokbelasting tnet Fourrier-reeksiU4Hz 7Hz 10Hzf~EErnoo'8 Belasting door rijdende vrachtwagen tnet bijbehorendeFourriertransfortnatieCement 1992 nr. 5Hierin is Fo de amplitude en OJ de hoekfrequentie die wordtuitgedrukt in [rad/slo Vaak wordt ook gewerkt met de 'gewo-ne' frequentief = 1/T,waarbij Tde periode van sin(OJt) voor-stelt.Via OJT = 2Jl geldtdusf= OJ/2Jl.Deeenheid vanfis [Hz]= [1/s].Zuivere harmonische belastingen komen strikt genomen na-tuurlijkweinig voor. In een aantal gevallenlevert het tochwelbruikbare schematiseringen op, bijvoorbeeld bij sommigemachines en bij doorwind en stromingge?nduceerde wervel-belasting.Periodieke belastingenDe belasting F(t) is periodiek, met een periode T, als voor elkewaarde van tgeldt dat F(t) = F(t+T). Dit impliceertdat F(t} inprincipe gedefinieerd is van t = - 00 tot t = 00. Uit de wis-kunde is bekend datdergelijke functies te schrijvenzijnals eensom van harmonische termen (de Fourier-reeks):00F(t) = ao + L [an cos (nOJt) + bn sin (nOJt) ]n=1met OJ = 2n / T. De co?ffici?nten an volgen uit:an = ~ orF(t) cos (nOJt) dt n = 1, 2, 3, .. 00(5)(6)Voor de co?ffici?nten bn gelden soortgelijke formules, maardan met de sinus in plaats van de cosinus; de co?ffici?nt aoisgewoon het gemiddelde van F(t). Neem als voorbeeld een re-gelmatige blokbelasting met periode T en topwaarde Fo, diesymmetrisch is ten opzichte van de lijn t = o.Hiervoor wordt met behulp van formule (6) gevonden:4 1 1F(t) = nFo [cos (OJt) - 3 cos (3OJt) + "5 cos (5OJt)-1"7 cos (7OJt) ....In figuur 7 is het resultaatvoor de eerste twee termen gegeven.Voorbeeldenvanperiodiekebelastingenzijnbelastingendoorlopende of springende personen en meer gecompliceerde(zuiger)machines. Een periodieke belasting kan aanleidinggeven tot hinderlijke opslingeringenzodra ??n van de aanwe-zige frequenties overeenkomt met ??n van de in het systeemvoorkomende eigenfrequenties.Transient belastingTransient betekent 'kortstondig' of'voorbijgaand', waarbij tedenken valt aan: botsingen, explosies, aardbevingen, passagevan eenenkelevrachtwagen,eenenkele heiklapenz.Dergelij-ke belastingen kunnen dus benaderd en geanalyseerd wordenals een reeks pulsen. In principe is het ook mogelijk van eentransient signaal een voorstelling in het frequentiedomein temaken. Wellichtheeft dat nietzoveel voordelenvoor de bere-kening, maar het kan helpen om inzicht te krijgen in de fre-quenties die in de belasting aanwezig zijn.In principe valt een transient belasting niet als een Fourier-reeks te presenteren, maar wel als een 'Fouriertransformatie'.In feite is dit eenlimietgeval van de reeks. In complexe notatiemet i2= -1 is de definitie daarvoor:+00 +00slOJ) = f F(t) exp (iOJt) dt = f F(t) cos (OJt) dt+-00 -00+00i f F(t) sin (OJt) dt (7)-00De eerste term is te vergelijken met de a-co?ffici?nten uit de17ICONSTRUCTIEF ONTWERPFourierreeks ende tweede termmetde b-co?ffici?nten. Merk Sop dat de Fouriergetransformeerde de dimensie heeft vankracht maal tijd, terwijl de Fourierco?ffici?nten de dimensiehebben van Fzelf. Figuur 8 geeft een voorbeeld van een ver-keersbelasting en de bijbehorende Fouriergetransformeerde.Duidelijk is te zien waar zich de belangrijke frequenties be-vinden.PulsbelastingDe puls is de ge?dealiseerde transient belasting, waarbij eenoneindig grote kracht optreedt in een oneindig korte tijd. Deintegraal So = f F(t)dtgeeft de waarde van de puls. Deze sche-matisering is bruikbaar voor tal van botsings- en explosiebe-lastingen. Of een dergelijke schematisering nauwkeurig ge-noeg is, hangt natuurlijk ook afvan de eigenschappen van deconstructie, vooral van de verhouding tussen de duur van hetverschijnsel en de eigentrillingstijden.Interessant is de frequentie-inhoud van de puls. Voor eenpulsbelasting op t = ?geldt dat F(t)alleen ongelijk nul is in debuurt van t = 0. In vergelijking (7) mag dus cos(wt) = 1,0 ensin(wt) = 0,0 worden gesteld, zodat:SF = f F(t)dt = SoWjrandomgenerator-10.0 +--+--+-+--+--+-+-+--+--+---'o 5 10 15 20 25 30 35 40 45 SO SHet spectrum is dus constant met een waarde die gelijk is aande puls zelf. Met anderewoorden: hetspectrum is onafhanke-lijk van wen in een pulsbelasting zijn dus alle frequenties ge-lijkmatig vertegenwoordigd. Als zodanig is de puls dus eenvolledige tegenhanger van de harmonische belasting, waarin I - - - - - - - - - - - - - - - - - - - - - - - - - jmaar een enkele frequentie aanwezig is. 9 Model voor random belasting, voorbeeld met N = 10Stochastische modellenStationaire processenKenmerk van een stationair stochastisch proces is dat het zichuitstrekt overde gehele tijdas, zonderdat eenbepaald patroonzich eenmaal exact herhaalt. We zouden kunnen spreken vaneenperiodiekebelasting meteen oneindig lange periode. Sto-chastische processen kunnen zodoende worden gemodel-leerd als een (oneindige) som van sinussen. Elke sinus heeftdaarbij zijn eigen amplitude Xk en frequentie ~ (vergelijkbaarmet de Fourier-reeks). Het stochastische karakter van dezebelastingenwordt gemodelleerd door de fasehoek 0 k voor ie-dere sinus stochastisch te nemen:Nx(t) = L Xk sin (Wkt + ~k) = L Xk (t) (8)k=la2 = fX2(t)dt= fLLxkxjsin(wkt+~k) sin(wi+~j)=L~n (~Bij de laatste stap is gebruik gemaakt van het feit datfsin(wkt+ ~k)sin(w}+ ~J dt = Ovoori # j.Via (9)volgtdan:a2 = L SFF(wJLlw = f SFF(W)dwHet oppervlak onder SFF is dus gelijk aan de variantie,vandaarde naam variantiespectrum. Nog niet is verteld hoe in een be-paald geval aanditspectrumwordtgekomen. Steldatergedu-rende eenvoldoende lange tijd Teen bepaalde belasting is ge-registreerd. Het variantie-spectrum SFF volgt dan uit:~ = stochastische fasehoek, die elke waarde tussen ?en 2n SFF = ~ SF stmet evenveel kans kan aannemen (uniforme verdeling)(11)De waarden van Xk volgen uit het zogeheten variatiespectrumSFF(W) van de belasting via (ziefig. 9):(9)De waarden van ~ moeten zodanig worden gekozen dat eenvoor het doel geschikte benadering ontstaat. Het is moeilijkdaarvoor algemene regels te geven. In figuur 9 is een voor-beeld gegeven met N = 10.Als Nheel groot wordt, bijvoorbeeld 100 of 1000, dan nadertdeverdelingvan het proces x(t)toteen normaleverdeling. De-ze uitspraak is gebaseerd op de centrale lirnietstelling uit destatistiek.Bezienin het tijdsdomein is het gemiddelde van dieverdeling nul (het zijn immers allemaal sinusfuncties), terwijlde variantie (standaardaEvvijking in het kwadraat) gegevenwordt door:18Hierbij is spde Fouriergetransformeerdevolgens (7) ensp'zijncomplex toegevoegde, dat wil zeggen dat in (7) + i vervangenwordtdoor -i. Hetbewijsvan(11)valtbuitenhetbestekvanditartikel.Evenals de periodieke belasting is de stochastische belastingdus opgebouwd te denken als een som van sinus- en consi-nusfuncties. Ook hierbij kan de responsie dus worden bere-kend door eerst iedere harmonische functie op zich te be-schouwen en dan de resultaten op te tellen. Dit staat bekendals de spectraalanalyse. Uiteraard kan dit alleen bij lineaire sys-temen.Als het constructiesysteem niet lineair is zal men een grootaantal functies moeten genereren, van elke gegeneerde belas-ting de responsie in het tijdsdomein berekenen entenslotte de responsies statistisch analyseren. Men spreekt danvan simulatie.Cement 1992 nr. 5x _ _~L-------=:::"-___10 Bloksgewijs stationair random proces11)fTransient random proces als prodnkt van een stationairproces en een intensiteitsfunctieII I----/Inte~acties tussen constructie en omgevingDevergelijkingvoorhetuitvoerenvaneendynamica-bereke-ning voor een systeem met meer vrijheidsgraden luidt:[M]!! + [C]1i + [K].!:! = E{t) (12)Devorm is in beginsel gelijk aan de vergelijking voor het ??n-massa-demper-veer-systeem. Hetverschil is datde desymbo-len M, C en K nu matrices voorstellen en dat u en Fvectorenzijn.Voorhetopstellenvan de matrices M, CenKzijn, mathe-matisch bezien, beproefde technieken bekend, zoals ondermeer de eindige-elementenmethode.Uitbreiding van (12) tot niet-lineair gedrag behoort tot demogelijkheden. Hierop en op de methoden om hetstelselver-gelijkingenop te lossenwordtineenafzonderlijkartikel inge-gegaan.Op het eerste gezicht lijkt het alsofin (12) links de constructiestaat(al dan nietmetinbegrip vande ondergrond) en rechts debelasting als een daarvan onafhankelijke grootheid.Toch is dat vaak niet waar. In veel gevallen treedt er een nietverwaarloosbare interactie op tussen de grootte van de belas-ting en de responsie van de constructie.Beschouw als eenvoudig voorbeeld van een interactiepro-bleem een botsing van een vrachtwagen met een constructie.Het is nauwelijks mogelijk eerst de botsingskrachten te bepa-len en daarna de responsie van de constructie te analyseren.Deze krachten hangen namelijk afvan zowel de eigenschap-12pen van de vrachtwagen als de eigenschappen van de con-Modellering van een botsingsprobleem structie. Hetis dusbetereenmodel te makenvanvrachtwagenL-_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _---' en constructie gezamenlijk, zoals aangegeven in figuur 12. OpBloksgewijs stationaireprocessenEen stationair stochastisch proces in de strikte zin van hetwoord komt natuurlijk niet voor. In de meeste gevallen issprake van processen waarvan de statistische eigenschappenlangzaamin de tijd veranderen. Meestalworden die processeng~modelleerd als een opeenvolging van stationaire blokken(fig. 10). In elkblok kunnen dan dus de statistische eigenschap-pen, met name het spectrum, verschillen.voorbeelden van deze belastingen zijn wind en golven. Bijwind worden blokken van 10 minuten of 1 uur genomen. Bijgolven heet zo'n stationair blok een sea state. Meestal wordtdaarvoor een duur van 3 tot 6 uur genomen. Er wordt vanuitgegaan dat de overgangen tussen de blokken zo geleidelijkzijn, dater geen noemenswaardige instelverschijnselenoptre-den.TransientprocessenOok transient belastingen als aardbevingen en heitrillingenkunnen als random processenworden gemodelleerd. Deeen-voudigste modellering is uit te gaan van een stationair procesen dit te vermenigvuldigen met een in de tijd verlopende in-tensiteitsfunctie. Deze functie is nul voor en na hetverschijn-sel (fig. 11). Tijdens de belasting kan de waarde constant zijn,maar uiteraard ook variabel.Het kenmerk van een transient belasting is dat het instelver-schijnsel een rol speelt. Soms is het mogelijk om hier op eenanalytischewijze rekeningmee te houden. Inde meeste geval-lenzal menzijn toevlucht nemen tot simulatie. Inwezenis datook wat gebeurt bij een groot aantal aardbevingsbe-rekeningen: men neemt een ofmeer registraties van aardbe-vingen (werkelijk of gegenereerd) en berekent het bijbeho-rende gedrag van de constructie.Cement 1992 nr. 5t = 0 wordt in dit model aan de vrachtwagen een snelheid vgegeven. De krachtvector F(t) in (12) blijft gewoon gelijk aannul voor alle waarden van t.Ookingevalvanbelastingdoor(bewegende) luchtofvloeistofhangt de grootte van de belasting vaak afvan de responsie vande constructie. Na het voorgaande niet zo vreemd, want opmoleculaire schaal zijn het natuurlijk ook gewoon botsingen.In sommige gevallen is het mogelijk de omgevende lucht ofvloeistofsamen met de constructie in een model mee te ne-men, maarmeestal is dat toch te bewerkelijk. Vaakis echter debelasting, inclusief zijn interactie, in analytische vorm be-kend, zoals bijvoorbeeld de (verdeelde) belasting van een be-wegende vloeistofop een staaf:f(t) = t pD CD Iv-ui (v-u) + pA {CM! V+ CM2 (iJ-?)}(13)Hierin is A het oppervlak van de doorsnede van de staaf, D deafmeting, p de massadichtheid van het water en v de onge-stoorde snelheid van de waterdeeltjes; ~, CM! en 4t2 zijnco?ffici?nten. Door de termen met ? naar de termen met m?aan de andere kant van de vergelijking te btengen en alle ter-men met unaar termen met cu, is deze vergelijking op te los-sen. Er ontstaat op die manier een hydrodynamische (ofaero-dynamische) massa en dito demping.Het toppunt op het gebied van interacties wordt geleverd bijverschijnselen als galoppingenflutter. Dezekunnenoptredenbij flexibele of verend opgehangen staven in een constantelucht of vloeistofstroom. Zolang de constructie perfect stilstaat, is er (loodrecht op de luchtstroom) geen enkele belas-ting.Zodra de constructie echterloodrecht op de luchtstroombegint te bewegen, wordt ogenblikkelijk een belasting opge-roepen die, afhankelijk van de staafvorm, de beweging ver-19ICONSTRUCTIEF ONTWERPsterkt ofverzwakt. Het eerste is natuurlijk vooral van belang.De belastingsterm bestaat in dit soort gevallen alleen uit ter-men met Uen u. In de meest eenvoudige en gelineariseerdevorm:m? + cu + ku = bu ofwel m? + (c-bJu + ku = 0 (14)----De co?ffici?nt bhangt bijvoorbeeld afvan de stroomsnelheid.Bij een bepaalde waarde van de stroomsnelheid kan bgroter 13d d d f dModellering van een heitrillingsprobleemwor en an c. De constructie is an negatie ge empt en er L-_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _~treedt bij de kleinste verstoring opslingering op. Het ver-schijnsel kan zich onder meer voordoen bij slanke bruggen.Een geheel ander soort interactie treedt op bij belasting doorlopende, dansende ofspringende personen. Devraag hierbij iswatde mensen doenals zij debewegingvande constructie op-merken. Wordt men bang ofjuist overmoedig? De interactieis hier dus van psychologische aard. Bij popconcerten in hetFeyenoordstadion wordt in ieder geval het zekere voor hetonzekere genomen: de responsie wordt gemeten en zonodigworden de bassen uit de muziek gehaald.Tenslotte zijn er de belastingen die aangrijpen via de onder-grond, zoals bij aardbeving, verkeerstrillingen, heitrillingen,een machine in een aangrenzend gebouw enz. In dat gevalontstaat er voor de grond een dubbelro1. Enerzijds is het on-derdeel van de constructie, anderzijds is het een deel van debron. Dezedubbelrol kan tot gecompliceerde interacties aan-leiding geven. Indeideale analyseworden bron, bodemenge-bouw in ??n totaal model gevangen, zoals aangegeven in fi-guur 13. Dit leidt echter tot dure en weinig inzichtelijke re-kenmodellen.In de praktijk wordt daarom meestal geprobeerd eerst teschatten wat het effect is van de bron in de ongestoorde bo-dem, datwil dus zeggen alsofde constructie er niet is. Vervol-gens wordt deze verstoring als voorgeschreven verplaatsingopgelegd aan het contructie-grond-systeem. De grootte vande fout die dan wordt gemaakt is nog punt van onderzoek.Beoordeling van de responsieDe responsie van een dynamisch belaste constructie is een va-ri?rende verplaatsing, een vari?rende spanning ofiets derge-lijks.Beoordeelddient teworden ofdeze responsie acceptabelis. Net als bij statischbelasteconstructies moetbij de beoorde-ling onderscheid worden gemaakt tussen uiterste grenstoe-standen en bruikbaarheidsgrenstoestanden. In veel gevallengaat het bij trillingsbeoordeling om de bruikbaarheid van eenbouwwerk: hinderlijkheid voor personen, scheuren in pleis-terwerk, onbruikbaar worden van gevoelige apparatuur(elektronenmicroscopen, computers) enz. Maar er zijn ookvoorbeelden waarbij de uiterste grenstoestand van een con-structie in het geding is: vermoeiing van een offshore con-s~ructie, bezwijken door aardbevingen, botsingen en explo-Sles.Voor de beoordeling van constructieve schade aan gebouwendient naar de opgewekte spanningen te worden gekeken. Bijberekeningen gebeurt dit ook meestal. In de praktijk wordthet trillingsniveau echter ookvaakvia een meting aan een be-staande constructie vastgesteld. Aangezien snelheden (ver-snellingen) eenvoudiger te meten zijn dan spanningen (rek-ken), zijn er ook criteria geformuleerd voor schade in termenvan snelheden.Een redelijke maat blijkt te zijn dat (lichte) schade verwachtmoetwordenbij snelheden hoger dan 5 ? 10 mrn!s. Uiteraardhoudtditooktennauwsteverband metde duurvan de trillin-gen. Theoretisch is overigens een verband tussen de spanning20en de snelheid aan te tonen. Trillingshinderenschade aan ap-paratuur laten zich ook redelijk vastleggen door middel vaneen snelheidscriterium. Door SBRworden momenteel op ditgebied richtlijnen voorbereid.Vaak moet bij de beoordeling van schade worden uitgegaanvan de maximale waarde van de responsie gedurende een be-paalde periode T. Bij een deterministische belasting is dit inbeginsel gewoon uit te rekenen. Als het gaat om een randomproces valt het maximum echter niet met 'zekerheid' te voor-spellen. wel kan een verwachtingswaarde worden afgeleid.Een vaak bruikbare formule is dan:x= x+gox metg = J(2InfoT,..) (15)Hierin is xde gemiddelde responsie (verplaatsing, snelheid,spanning), 0x de standaardafwijking,Jo de centrale frequentieen T,.. de duur van de beschouwde periode.Als de uitkomstvan debeoordeling negatiefis, als dus het tril-lingsniveau onaanvaardbaarwordt gevonden, zal het ontwerpgewijzigd moeten worden of zullen anderzins maatregelengetroffen moeten worden. De mogelijkheden zijn velerlei:- wijzigen van de stijfheid ofmassaverdeling in de construc-tie;- opvoeren van demping, al dan niet kunstmatig;- aanpassen van de vorm van de constructie;- afschermen ofisoleren van de constructie;- isoleren van gevoelige apparatuur;- be?nvloeden ofisoleren van de trillingsbron;- monitoren en bewaken van de responsie;- inspecteren op schade.De keuze hangt afvan de omstandigheden.Hetwijzigenvan de constructie kan makkelijker op de teken-tafel dan in een bestaande situatie. Soms wordt niet de con-structie ontworpen, maar de bron: er wordt een nieuwe ma-chine aangeschaft, de keuze valt op heien in plaats van boren,er wordt een spoorbaan aangelegd enz. Een algemeen receptvalt niet te geven, maar het is plezierig te weten dat er vele pa-rameters zijn die te be?nvloeden zijn.Ten slotteIn dit artikel is ingegaan op de berekening enbeoordelingvandynamisch belaste constructies. Gegeven de beschikbareruimtekondatnietanders danbeknoptzijn.Nietgesprokenisbijvoorbeeld over de modellering van de constructie zelf, demateriaaleigenschappenonderdynamische omstandigheden,de demping, de beschikbare berekeningstechnieken, het ge-bruik van experimentele modellen.Op zichzelf genomen zal dit artikel daarom weinig houvastgeven voor wie daadwerkelijk een dynamica-analyse wil uit-voeren. Maar datwas het doel ook niet. Het doel was een aan-tal begrippen te introduceren en een overzicht te schetsen, alsbasis voor de verdere artikelen in deze reeks. Daarin zal in eenaantal opzichtenmeerconcreetop detailswordeningegaan, alzal ook dan vaak een verdere doorverwijzing naar de litera-tuur onvermijdelijk blijken te zijn.Cement 1992 nr. 5IUTILITEITSBOUW I IPREFABRICAGE IEKON-SYSTEEM GEEFTRUIMTE AAN GEBRUIKERS ENONTWERPERS (11)prof.ir.H.W.Bennenk, TU Eindhoven en Schokbeton BVir.P. van Boom, Schokbeton BVIn Cement 1992, nr. 2 is het Ekon-systeem gepresenteerd. Hierin is naast deuitgangspunten een omschrijving gegeven van de onderdelen en is ingegaan op desamenwerking tussen vloer en balk via de voeg. In dit artikel wordt nader ingegaanop de verbinding tussen balk en kolom. Daarnaast wordt verslag gedaan van heteerste project dat met het Ekon-systeem is uitgevoerd.BALK-KOLOMVERBINDINGBijhet ontwerpen van het Ekon-systeem was het vermijden vanuitwendigeconsoleseenbelang-rijk punt van studie.voorgespannen kolommen, waarbij deconsoles achteraf moeten worden aan-gestort.gebruik was op dat moment niet zogroot en infeite meer gerichtop het op-bouwen van ervaring om de ontwikke-ling te kunnen voltooien. Na ampele af-wegingen is gekozen voor de in Noor-wegen ontwikkelde BSF-console, inplaats van de console die in Finlandwerd uitgeprobeerd. Van deze laatstge-noemde console wordt in figuur 1 eenVoordeklantkanhetbelangrijkzijn, dater geen uitwendige consoles voorko-men. Voordeproducentkanhetbelang-rijk zijn kolommen zonder aange-bouwde consoles te maken, zeker bijDaarnaast moet heel nuchter wordengekeken naardeintegraleconsequentiesen de kosten. Schokbeton was in de ge-lukkige omstandigheid dat er binnenPartek Concrete een tweetal typen sta-len consoles in ontwikkeling was. Het- , - - - , --'--- - --1 In Finland ontwikkelde verbindingLiteratuur1. Collegedictaten b7, b8, b9 en bIS, TU Delft, Afdeling Ci-viele Techniek.2. CUR-rapporten 57 en 75.3. Meet- en beoordelingsrichtlijnen voor schade, hinder enbe?nvloeding gevoelige apparatuur door trillingen (3 delen),SBR, Rotterdam (nog te verschijnen).4. Smith,].W., Vibration ofStructures, Applications in civilengineering design. Chapman and Hall, London, New Vork,1988.5. Timoshenko, S.P., Young, D.H. and Weaver, w., VibrationCement 1992 nr. 5r - - - -I= I1'---- - -2 In Noorwegen ontwikkelde BSF-verbindingproblems in Engineering. D. van Nostrant, Princeton, USA,1974.6. Den Hartog, ].P., Mechanical Vibrations. McGraw-HillBook Co., New Vork.7. Clough, RW. and Penzien,]., Dynamics of Structures.McGraw-Hill Kogakusha Ltd., Tokyo.8. CrandalL S.H. and Mark, W.D., Random Vibration in Me-chanical Systems. Academic Press, New Vork, 1963.9. Papoulis, A., Probability, Random Variables and StochasticProcesses. McGraw-Hill, Kogakusha Ltd., 1965.21