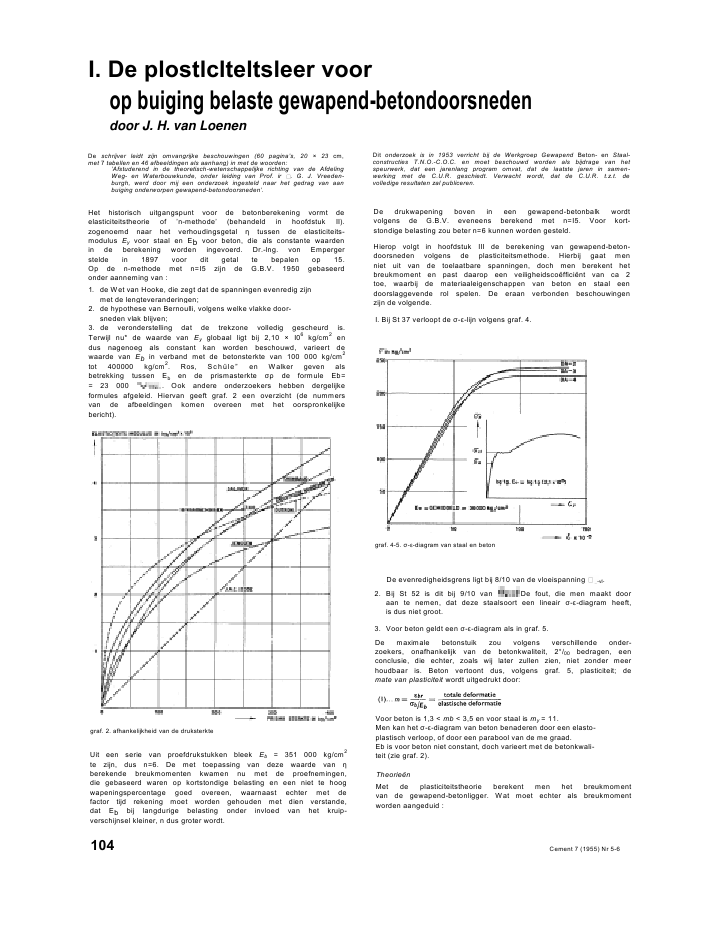
I. De plostlclteltsleer oorop buiging belaste gewapend-betondoorsnedendoor J. H. van LoenenDe schrijver leidt zijn omvangrijke beschouwingen (60 pagina's, 20 ? 23 cm,met 7 tabellen en 46 afbeeldingen als aanhang) in met de woorden:'Afstuderend in de theoretisch-wetenschappelijke richting van de AfdelingWeg- en Waterbouwkunde, onder leiding van Prof. ir . G. J. Vreeden-burgh, werd door mij een onderzoek ingesteld naar het gedrag van aanbuiging onderworpen gewapend-betondoorsneden'.Het historisch uitgangspunt voor de betonberekening vormt deelasticiteitstheorie of 'n-methode' (behandeld in hoofdstuk II).zogenoemd naar het verhoudingsgetal tussen de elasticiteits-modulus Ey voor staal en Eb voor beton, die als constante waardenin de berekening worden ingevoerd. Dr.-lng. von Empergerstelde in 1897 voor dit getal te bepalen op 15.Op de n-methode met n=5 zijn de G.B.V. 1950 gebaseerdonder aanneming van :1. de Wet van Hooke, die zegt dat de spanningen evenredig zijnmet de lengteveranderingen;2. de hypothese van Bernoulli, volgens welke vlakke door-sneden vlak blijven;3. de veronderstelling dat de trekzone volledig gescheurd is.Terwijl nu* de waarde van Ey globaal ligt bij 2,10 ? I06kg/cm2endus nagenoeg als constant kan worden beschouwd, varieert dewaarde van Eb in verband met de betonsterkte van 100 000 kg/cm2tot 400000 kg/cm2. Ros, Sch?le" en Walker geven alsbetrekking tussen Eb en de prismasterkte de formule Eb== 23 000 . Ook andere onderzoekers hebben dergelijkeformules afgeleid. Hiervan geeft graf. 2 een overzicht (de nummersvan de afbeeldingen komen overeen met het oorspronkelijkebericht).graf. 2. afhankelijkheid van de druksterkteUit een serie van proefdrukstukken bleek Eb = 351 000 kg/cm2te zijn, dus n=6. De met toepassing van deze waarde van berekende breukmomenten kwamen nu met de proefnemingen,die gebaseerd waren op kortstondige belasting en een niet te hoogwapeningspercentage goed overeen, waarnaast echter met defactor tijd rekening moet worden gehouden met dien verstande,dat Eb bij langdurige belasting onder invloed van het kruip-verschijnsel kleiner, n dus groter wordt.Dit onderzoek is in 1953 verricht bij de Werkgroep Gewapend Beton- en Staal-constructies T.N.O.-C.O.C. en moet beschouwd worden als bijdrage van hetspeurwerk, dat een jarenlang program omvat, dat de laatste jaren in samen-werking met de C.U.R. geschiedt. Verwacht wordt, dat de C.U.R. t.z.t. devolledige resultaten zal publiceren.De drukwapening boven in een gewapend-betonbalk wordtvolgens de G.B.V. eveneens berekend met n=5. Voor kort-stondige belasting zou beter n=6 kunnen worden gesteld.Hierop volgt in hoofdstuk III de berekening van gewapend-beton-doorsneden volgens de plasticiteitsmethode. Hierbij gaat menniet uit van de toelaatbare spanningen, doch men berekent hetbreukmoment en past daarop een veiligheidsco?ffici?nt van ca 2toe, waarbij de materiaaleigenschappen van beton en staal eendoorslaggevende rol spelen. De eraan verbonden beschouwingenzijn de volgende.I. Bij St 37 verloopt de --lijn volgens graf. 4.graf. 4-5. --diagram van staal en betonDe evenredigheidsgrens ligt bij 8/10 van de vloeispanning -vl.2. Bij St 52 is dit bij 9/10 van De fout, die men maakt dooraan te nemen, dat deze staalsoort een lineair --diagram heeft,is dus niet groot.3. Voor beton geldt een --diagram als in graf. 5.De maximale betonstuik zou volgens verschillende onder-zoekers, onafhankelijk van de betonkwaliteit, 2?/00 bedragen, eenconclusie, die echter, zoals wij later zullen zien, niet zonder meerhoudbaar is. Beton vertoont dus, volgens graf. 5, plasticiteit; demate van plasticiteit wordt uitgedrukt door:Voor beton is 1,3 < mb < 3,5 en voor staal is my = 11.Men kan het --diagram van beton benaderen door een elasto-plastisch verloop, of door een parabool van de me graad.Eb is voor beton niet constant, doch varieert met de betonkwali-teit (zie graf. 2).Theorie?nMet de plasticiteitstheorie berekent men het breukmomentvan de gewapend-betonligger. Wat moet echter als breukmomentworden aangeduid :104 Cement 7 (1955) Nr 5-61. het moment, waarbij de eerste scheuren optreden ?2. het moment, waarbij de scheuren zo groot worden, dat hetwapeningsstaal op de duur zal corroderen?3. het moment, waarbij de constructie zo sterk vervormt, datzij niet meer bruikbaar is voor het aan haar gestelde doel?4. het moment, waarbij de constructie zal bezwijken, als debelasting voldoende lange tijd constant wordt gehouden?5. het moment, waarbij de constructie ogenblikkelijk volledigbezwijkt ?Als breukmoment neemt men in dit rapport aan de maximale be-lasting, die bet proefstuk tijdens de kortstondige beproeving heeftgehouden.De plasticiteitstheorie?n zijn nu te splitsen in twee groepen:Groep IKenmerkend zijn hier:1. in de plaats van een driehoekige spanningsverdeling, zoals dievolgt uit de wet van Hooke, wordt de spanningsverdeling inde drukzone voorgesteld door een gelijkvormig getransfor-meerd ff- -diagram;2. de hypothese van Bernoulli is van toepassing;3. ondersteld wordt, dat de trekzone gescheurd is.Aangezien de drukkracht evenwicht moet maken met de trek-kracht in het wapeningsstaal, is de grootte van de drukfiguurvastgelegd en hiermee ook de plaats van de neutrale lijn. Hetvolgende kan zich voordoen.Als de balk bezwijkt door overschrijding van de maximale beton-stuik is hiermee de maximale vastgelegd ; uit het evenwichtmet de trekkracht in het staal volgt de plaats van de neutrale lijn.Als de balk bezwijkt door vloeien van het staal, dan is de rek inde staalvezel bekend; hieruit is dan de hoogte van de neutralelijn te bepalen.Groep IIKenmerkend zijn hier:1. op het ogenblik van breuk is de betondrukzone volledigplastisch gedeformeerd, dus in alle vezels, waar druk heerst,is ook de maximale betonspanning aanwezig;2. ondersteld wordt, dat de trekzone gescheurd is.Breuk treedt op, wanneer de staalspanningen de vloeigrenshebben bereikt. Dan zijn dus de maximale beton- en staalspan-ning bekend; uit de evenwichtsvoorwaarde volgt dan de plaatsvan de neutrale lijn. Volgens de theorie?n van deze groep heefthet staal in het breukstadium gevloeid. Dit is alleen het geval bijniet overgedimensionneerde balken. Deze theorie?n zijn dus integenstelling met groep I niet universeel geldig.Bij lage wapeningspercentages blijkt het breukmoment echterbij de proef hoger te zijn, dan uit de theorie zou volgen. Ditverschijnsel wordt versteviging genoemd en in hoofdstuk IVnader behandeld.Wij gaan terug naar Groep ITot deze groep behoren een veertiental theorie?n.a. Indien de balk licht gewapend is, dan gelden als grenzen devloeispanning en de vloeirek van het staal.b. Indien de balk zwaar gewapend is en bij druk in de bovenstevezel bezwijkt, dan is de maximale stuik s zeer belangrijk.De verschillende theorie?n geven dan ook of een vaste waardeervoor, of een waarde die varieert met de betonsterkte, zieOm economische redenen is de belangstelling tegenwoordigmeer gericht op de betonliggers met laag wapeningspercentage;hierbij speelt de variatie van s een minder belangrijke rol,zodat de verschillende theorie?n toch zeer bevredigend overeen-stemmende waarden opleveren. In de verschillende formulesworden de betonsterkte en de aYs/l van het staal ingevoerd, zodatmen deze van te voren moet kennen.Om de berekening te vereenvoudigen en de verschillende theorie?nonderling te kunnen vergelijken, heeft men de grootheden en ingevoerd.Met de co?ffici?nt ? geeft men de 'V?lligkeit' van de betondruk-zone aan :D = ? x. b. bDe waarde voor beweegt zich tussen I/2 voor een driehoekig--verloop en I voor een volledig plastisch verloop. Voor a?,voeren verschillende onderzoekers de kubussterkte, de prisma-sterkte, de cylindersterkte of een deel daarvan in.De factor legt de plaats van de drukresultante t.o.v. de boven-kant van de balk vast.Z'=x.?(zietek.9)Bepaling van x:a. de balk bezwijkt bij overschrijding van de betonstuik; dan is4 = 4S(2) ....... Bernoulli:x= ?bs.h'Het breukmoment wordt nu gevonden als product van de kracht-arm maal de drukkracht D. Uit tek. 9 volgt:Z = h' -- Z' = h'--{?.xUit (2) en (3) kan bepaald en gesubstitueerd worden in deformules; voor D en vinden we het breukmoment:(4)....Mbr = (h'--?.x).b.x.oc.abb, de balk bezwijkt bij vloeien van het staal; dan is:CTy gelijk aan 2 400 kg/cm2(vloeigrens)De grootste betonstuik hangt dan samen met de vorm van het--diagram van het beton.Wij gaan over tot Groep II en vatten samen:1. in de gehele drukzone heerst de maximale betonspanning;2. aangenomen wordt, dat op het ogenblik, dat breuk optreedt,de vloeigrens in het staal is bereikt.De theorie?n van deze groep zijn slechts geldig voor niet over-gewapende balken; daarom wordt bij de verschillende theorie?nhet maximum wapeningspercentage vastgelegd, waarvoor detheorie nog geldt. Bij de berekeningswijze, zoals die is vastgelegdin de Russische gewapend-betonvoorschriften, wordt ook nogeen minimum wapening voorgeschreven, om bezwijken doorplotselinge breuk van het staal te voorkomen.Hierop behandelt de schrijver de proefstukken. Achter elkaarkomen de bepaling van de kubussterkte, de prisma- en cylinder-sterkte en de hierbij optredende verschijnselen ter sprake. Wilmen een storingvrij gebied ter beschikking hebben, dat even hoogals breed is, dan moet het proefstuk 3x zo hoog als breed zijn.Cylindrische proefstukken acht de schrijver minder aanbevelens-Cement 7 (1955) Nr 5-6 105waardig, om ermee het gedrag van prismatische balken te inter-preteren.Nuttig is het, prisma's excentrisch te belasten, zodat juist in hetene zijvlak de rekken nul zijn, een toestand die overeenkomt metde drukzone van een balk, die aan een vierpuntsbuigproef wordtonderworpen. Uit deze proefneming kunnen de co?ffici?nten en worden bepaald, als de excentriciteit e bekend is en d dediameter van het proefstuk.(Als kleinste afmeting van het proefstuk neme men liefst Sx degrootste korrel van het beton).Bedraagt de gemiddelde breukspanning, gemeten aan het excen-trisch belaste prisma br gemiddeld, en de breukspanning, ge-meten aan een centrisch belaste prisma, br, dan is:br gemiddeld = . br en(5) .......... = br gemiddeld/abrverder is . d = d/2 -- e(6) ....... dus = 1/2 -- e/dAfleiding van het theoretische breukmoment door T.N.O.Uit de proeven op de excentrisch belaste prisma, 10 10 x30 cm3,toegepast op niet overgedimensionneerde balken, werden deco?ffici?nten = 0,39; = 0,703; -- = 0,55 verkregen, die in-gevuld dienen te worden in formule:De door T.N.O. bepaalde waarde komt het beste overeen met detheorie, die in de Russische voorschriften is opgenomen.Voorts is de co?ffici?nt / langs theoretische weg voor eenelasto-plastisch en een parabolisch verloop van het --diagrambepaald. Het eindresultaat luidt:Voor de hier beschouwde proefnemingen van T.N.O. geldt, dathet inderdaad optredende breukmoment gemiddeld 6,6% hogeris dan het theoretische.Versteviging t.o.v. het theoretische breukmoment, hoofdstuk IV1. Theorie van So//ger; na versteviging is: ay = . ffy ?, gemiddeld = U4. De versteviging heeft dus haar oorzaakin het beter worden van koudgerekt staal.2. Al is de betondoorsnede gescheurd, toch zal de betontrekzonevlak onder de neutrale lijn nog trekspanningen opnemen.De invloed hiervan is echter zeer gering, dus te verwaarlozen.3. Emperger vestigde de aandacht erop, dat een wapeningsstaafomhuld met een dun laagje mortel bij een veel hogere rekscheuren vertoont dan bij normale breukrek van beton(4,08 ?/00 i.p.v. 0,13 ?/00!). Zelfs bij een dikte van 10 cm van demortellaag vindt men nog een verhoogde breukrek. Scheurt nude betondoorsnede, dan zal het beton, dat de staaf omringt,aan de staaf blijven kleven (zie tek. 26).Bij deze grote rek is het beton zeker plastisch en zal = 30kunnen worden gesteld. De invloed van dit verschijnsel is op8% berekend.4. Volgens Gebauer bestaat de mogelijkheid, dat t.g.v. krimp dewapeningsstaven met een bepaalde drukspanning voorgespan-nen zijn, waardoor het draagvermogen van de wapening resp.van de balk gunstig wordt be?nvloed.Als de meest waarschijnlijke oorzaak van de versteviging komtechter die onder sub 3 genoemde theorie van Emperger in aan-merking.De veiligheidsfactor, hoofdstuk VAls veiligheidsfactor wordt geen constant bedrag aangehouden,daar men door verschillende invloeden bij de ene constructie eengroter veiligheid wenst dan bij een andere constructie.De volgende factoren kunnen o.a. invloed hebben bij het bepalenvan de veiligheidsfactor:1. doel van de constructie;2. onderdeel van de constructie; zijn betekenis t.o.v. het draag"vermogen van de constructie;3. belasting, die op het onderdeel komt; verschil tussen rustendeen mobiele belasting;4. wapeningspercentage van de balk, die de aard van de breuksterk be?nvloedt;5. agressiviteit in fysisch en chemisch opzicht;6. gebruikte materialen;7. nauwkeurigheid, waarmee de berekening is gemaakt en waar-mee het werk wordt uitgevoerd (bouwcontr?le).Het is zeer moeilijk voor ieder in de practijk voorkomend gevaleen veiligheidsco?fficient bindend voor te schrijven. De bij de n-methode d.m.v. toelaatbare spanningen vast voorgeschrevenveiligheidsco?fficient is daarom aan de ene zijde gemakkelijk, maarleidt aan de andere kant tot oneconomische constructies, daar inde veiligheid de ongunstige gevallen verdisconteerd moetenworden. De methode van de Russische gewapend-betonvoor-schriften, waarbij voor de verschillende onderdelen van eenconstructie een 'richtgetal' als veiligheidsco?fficient wordt op-gegeven, verdient daarom de voorkeur:wijze van belasting hoofd-over-spanningkolommen anderedragendedelenhoofdbelasting ..........................hoofd belasting 4- wind +temperatuur ..............................hoofdbelasting+wind +temperatuur+krimp +alle andere invloeden ................2,5 (2,2)2,25(2,0)2,0 (l,6)2,2 (2,0)2,0 (l,8)I.8 (l,4)2,0 (l,8)l,8 (l,6)l,6 (l,3)Bij kolommen met een diameter kleiner dan 30 cm moeten dewaarden in kolom 2 met 25% worden verhoogd. De tussenhaakjes geplaatste waarden zijn afkomstig van de betonvoor-schriften van 1942, waarin rekening is gehouden met de nood-zakelijke besparing van cement en staal, een typisch voorbeeld,dat ook de tijdsomstandigheden de grootte van de veiligheids-co?fficient kunnen be?nvloeden.Uitbreiding en samenvatting, hoofdstuk VIDe toepassing van de plasticiteitsleer is uitgebreid op T-balken,dubbelzijdig gewapende balken en voorgespannen balken. Opdeze gevallen nader in te gaan ligt m.i. buiten het kader van dezebeknopte bespreking.Resumerend zegt de schrijver ten slotte het volgende:Met de plasticiteitsrekenmethode wordt een breukmoment be-rekend, dat goed in overeenstemming blijkt te zijn met hetbreukmoment, dat bij proeven wordt gevonden.De met de -methode gevonden breukmomenten wijken bij lagewapeningspercentages niet zo sterk van de proefresultaten af, datop grond hiervan de -methode moet worden verworpen.Bij de meeste plasticiteitsmethoden wordt alleen aandacht ge-schonken aan de sterkte van het constructieonderdeel, terwijldeformaties en scheurvorming hiermee niet worden beschreven.Alleen de theorie?n van Torroja, R?sch en Bittner voeren een'kritiek' stadium in, waarbij de vormveranderingen de doorslaggeven.Bij de -methode daarentegen zijn de toegelaten beton- en staal-spanningen zo gekozen --de practijk heeft dit geleerd-- dat hiergeen ontoelaatbare scheuren optreden.Bij langdurige belastingen zal door de kruip van het beton, dieevenredig is met de opgebrachte spanning, de spanningsverdelingveranderen en misschien wel de driehoekige spanningsverdelingbenaderen. De -methode zal dan een beter beeld van de span-ningsverdeling geven.De plasticiteitsmethode is daarom alleen academisch juist bij deuitwerking van proeven en bij constructies, waar de mobiele be-lasting overheersend is. In de practijk zal de plasticiteitstheorieechter een goede benadering geven voor de berekening van lang-durig belaste constructies.E. A. F. HuberDigest - Sommaire - Zusammenfassung p. 113106 Cement 7 (1955) Nr 5-6