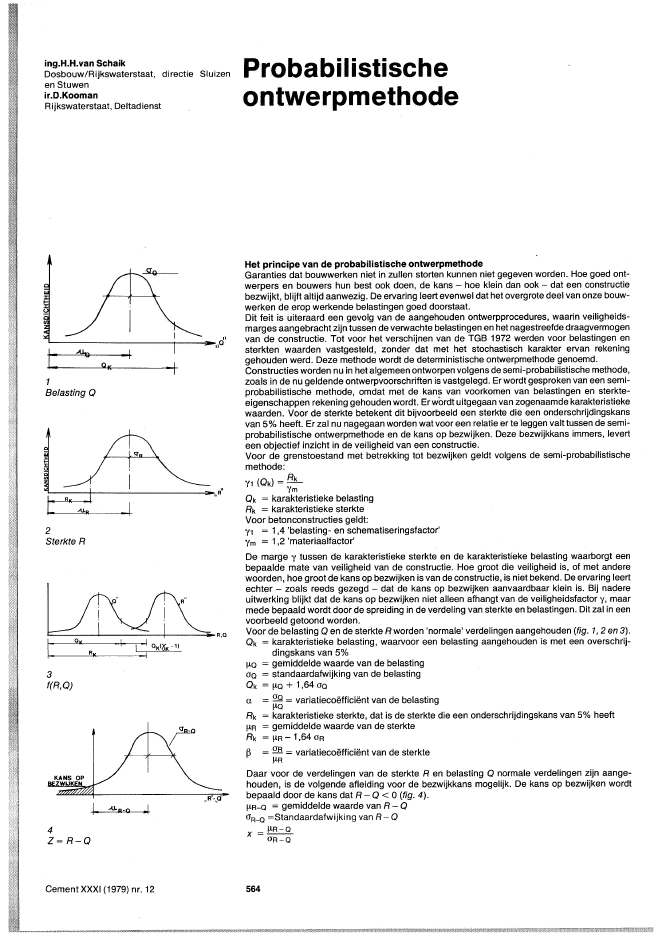
ing.H.H.van SchaikDosbouw/Rijkswaterstaat, directie Sluizenen Stuwenir.D.KoomanRijkswaterstaat, DeltadienstProbabilistischeontwerpmethodeHet principe van de probabilistische ontwerpmethodeGaranties dat bouwwerken niet in zullen storten kunnen niet gegeven worden. Hoe goed ont-werpers en bouwers hun best ook doen, de kans - hoe klein dan ook - dat een constructiebezwijkt, blijft altijd aanwezig. De ervaring leert evenwel dat het overgrote deel van onze bouw-werken de erop werkende belastingen goed doorstaat.Dit feit is uiteraard een gevolg van de aangehouden ontwerpprocedures, waarin veiligheids-marges aangebracht zijn tussen de verwachte belastingen en het nagestreefde draagvermogenvan de constructie. Tot voor het verschijnen van de TGB 1972 werden voor belastingen ensterkten waarden vastgesteld, zonder dat met het stochastisch karakter ervan rekeninggehouden werd. Deze methode wordt de deterministische ontwerpmethode genoemd.Constructies worden nu in het algemeen ontworpen volgens de semi-probabilistische methode,zoals in de nu geldende ontwerpvoorschriften is vastgelegd. Er wordt gesproken van een semi-probabilistische methode, omdat met de kans van voorkomen van belastingen en sterkte-eigenschappen rekening gehouden wordt. Er wordt uitgegaan van zogenaamde karakteristiekewaarden. Voor de sterkte betekent dit bijvoorbeeld een sterkte die een onderschrijdingskansvan 5% heeft. Er zal nu nagegaan worden wat voor een relatie er te leggen valt tussen de semi-probabilistische ontwerpmethode en de kans op bezwijken. Deze bezwijkkans immers, leverteen objectief inzicht in de veiligheid van een constructie.Voor de grenstoestand met betrekking tot bezwijken geldt volgens de semi-probabilistischemethode:Y1 (Ok) = BiLYmOk = karakteristieke belastingRk = karakteristieke sterkteVoor betonconstructies geldt:Y1 = 1,4 'belasting" en schematiseringsfactor'Ym = 1,2 'materiaalfactor'De marge y tussen de karakteristieke sterkte en de karakteristieke belasting waarborgt eenbepaalde mate van veiligheid van de constructie. Hoe groot die veiligheid is, of met anderewoorden, hoe grootde kans opbezwijken is van de constructie, is niet bekend. De ervaring leertechter - zoals reeds gezegd - dat de kans op bezwijken aanvaardbaar klein is. Bij nadereuitwerking blijkt dat de kans op bezwijken niet alleen afhangt van de veiligheidsfactor y, maarmede bepaald wordt door de spreiding in de verdeling van sterkte en belastingen. Dit zal in eenvoorbeeld getoond worden.Voor de belasting 0 en de sterkte Rworden 'normale' verdelingen aangehouden (fig. 1,2 en 3).Ok = karakteristieke belasting, waarvoor een belasting aangehouden is met een overschrij-dingskans van 5%[.lo = gemiddelde waarde van de belastingoa = standaardafwijking van de belastingOk = [.lo + 1,64 00cr = 00 = variatieco?ffici?nt van de belasting[.lORk = karakteristieke sterkte, dat is de sterkte die een onderschrijdingskans van 5% heeft/-lR = gemiddelde waarde van de sterkteRk = /-lR - 1,64 OR~ = OR = variatieco?ffici?nt van de sterkte[.lRDaar voor de verdelingen van de sterkte R en belasting 0 normale verdelingen zijn aange-houden, is de volgende afleiding voor de bezwijkkans mogelijk. De kans op bezwijken wordtbepaald door de kans dat R - 0 < 0 (fig. 4).[.lR-O = gemiddelde waarde van R - 0O"R_O =Standaardafwijking van R -- 0x = [.lR-O?R-O-I1--~~~~~~~~~~-r-~---'_I)dJt1Belasting 0I. A1. R- Q ..I4Z= R-OKANS OPZWIJKE3t(R,O)2Sterkte R:-~~~+-~~~~~~~~~-=-'I\AnCement XXXI (1979) nr. 12 5645Verband tussen bezwijkkans envariatieco?ffici?ntena = variatieco?ffici?nt belasting13 = variatieco?ffici?nt sterkteYk = Rk/Qk = 1,42 + f.l2 2 (1 + 1,64 a )2a I-' Yk 1-1 ,64 13(1+1,64a)_1Yk 1-1,64f:l2 + f.l2 2 (1 + 1,64 a)2a I-' Yk 1-1,6413Deze betrekking is in figuur 5 weergegeven.We zien dus dat bij gelijkblijvende veiligheidsco?ffici?nt Yk = ~~ de bezwijkkans sterk afhan-kelijk is van de spreiding in de verdeling van sterkte en belasting. Er lijkt dus veel voor te pleiten,even afgezien van de praktische problemen, een constructie op probabilistische wijze door terekenen. In het volgende hoofdstuk zal verder worden ingegaan op de probabilistische be"nadering van de hydraulische belastingen veroorzaakt door golf- en vervalkrachten, waarna ineen ander hoofdstuk een rekenvoorbeeld gegeven zal worden.Voor de bepaling van de kans dat R - Q < 0 is wordt x berekend uit de betrekkingf.lR-Q-X OR-Q = 0f.lR-Q = f.lR- f.lQOR-Q = VOd + o~ == Va2 f.l6 +f32~x = f.lR-Q= f.lR-f.lQOR-Q v'a2f.l6 + f32~Stel k = Rk = ffi. (1-1,6413)Y Qk f.lQ (1+1,64 a)_ 1+1,64af.lR - Yk f.lQ (1-1,64 13 )(1+ 1,64 a) _ 1Yk 1-1,6413xx0,30,22 k-::::~~~.J. h'v"-1'r0(:00.~;~.'i..De belastingenDe belastingen op de stormvloedkering bestaan hoofdzakelijk uit vervalbelastingen (statisch),veroorzaakt door verschil in waterstanden ter weerszijden van de kering, golfbelastingen meteen quasi-statisch karakter, veroorzaakt door het op zee voorkomende golfbeeld en dyna-mische belastingen, veroorzaakt door stroming en golfklappen.De kansverdeling van de belastingen is alleen bepaald voor de combinaties van verval- en golf-belasting. Dynamische belastingen zijn hierin niet meegenomen omdat er niet voldoende overbekend is. Deze worden dan ook op eenvoudige maar conservatieve wijze in de ontwerp-procedure meegenomen.NatuurrandvoorwaardenKansverdeling der vervallenDeze is voor ??n deel opgebouwd uit de kansverdeling van de hoogwaterstanden aan dezeezijde, gebaseerd op waarnemingen [3J, en gecorrigeerd voor de invloed van de Delta-werken. Hoewel hier niet essentieel: dit is een negatief exponenti?le verdeling. De anderecomponent is de kansverdeling van de waterstanden aan de Oosterscheldezijde van de storm-vloedkering. Deze is gebaseerd op de verdeling van (waargenomen)laagwaterstanden, dievoorafgaan aan hoge hoogwaterstanden; deze hoogwaterstanden zijn hoger dan dat peil dataanleiding geeft tot het sluiten van de stormvloedkering. De waargenomen laagwaterstandenzijn gecorrigeerd voor de aanwezigheid van de stormvloedkering, alsmede voor de invloed vanhet gesloten zijn van de stormvloedkering op de binnenwaterstand, zoals daardoor veroorzaak-te atwaaiing, translatiegolven die tijdens de sluiting ontstaan en dergelijke. Deze kansverdelingis een 'normale' Gaus-verdeling met een bepaalde f.l en o.Kansverdeling der golvenEen veel gebruikte methode om het onregelmatige golfbeeld op zee te beschrijven is de zgn.spectrale methode. Hierbij wordt een zgn. variantie"dichtheidsspectrum geconstrueerd op basisvan een in de tijd op ??n plaats geregistreerd waterstandsverloop. De waarnemingsperiodedient zo kort te zijn (orde van grootte 1 uur of minder) dat sprake is van een stationair golfbeeld;een voorwaarde voor een correcte statistische beschrijving van dit golfbeeld.Dit spectrum geeft in principe de verdeling van de in het golfbeeld aanwezige golfenergie pergolffrequentie weer; het spectrum wordt aangegeven met Snn. Deze spectrale beschrijvingvoorkomt dat alle aanwezige informatie over de combinaties van golfhoogten en golfperiodengedurende de berekeningen moet worden meegenomen. Dit zou een gigantische boekhoudingbetekenen. Daar tegenover staat dat bij de spectrale methode de informatie over de individuelegolven verloren gaat. Uitsluitend over de amplituden kan nog iets gezegd worden in termen vanwaarschijnlijkheid, alsmede over de gemiddelde periode.Het golfspectrum nabij de Oosterscheldekering wordt hoofdzakelijk door twee groothedenbepaald, namelijk de buitenwaterstand hw en de plaatselijke windsnelheid die gedurende 1 uurwordt overschreden Vwo Beide grootheden zijn stochastische variabelen (aangeduid met onder-streping) en in zekere mate gecorreleerd. Per hoogwaterstand is er dan ook een kansverdelingvan windsnelheden. Dus is er ook per hoogwaterstand een kansverdeling van golfspectra.Samen met de kansverdelingen van de hoogwaterstanden en de binnenwaterstanden is er dusCement XXXI (1979) nr. 12 565P-KANS-DICHTHEID...J...j....D(VARIABELE)een drie-dimensionale kansverdeling van de natuurrandvoorwaarden. Omdat het praktischer isom te werken met de afgeleide van de kansverdeling, de zgn. kansdichtheidsfunctie (kdf) dieaangeeft de kans dat de beschouwde variabele in het interval d(variabele)l?gt, wordt in hetvolgende veelvuldig met de kdf gewerkt en daarvan nog de numerieke benadering. De kans-verdeling is dan weer de integraal van de kdf (fig. 6).De drie-dimensionale kdf van de natuurrandvoorwaarden is dus:p{~ bws, Snn (hw, bws, Vw)} =P {hW (hw) } x P{ bws (bWSI hw = hw) } x p{Snn Ww\ hw = hW)} (1)Vw = windsnelheidDe spectra zelf zijn berekend met behulp van een mathematisch model dat als variabelen debuitenwaterstand, de windsnelheid en de bodemdiepte heeft. Het model is aan de beschikbarewaarnemingen getoetst.OverdrachtsfunctiesDe belastingen op een constructie worden enerzijds bepaald door de natuurrandvoorwaardenen anderzijds door de eigenschappen van de constructie zelf. Omdat uitsluitend statische enquasi-statische belastingen beschouwd worden, is alleen de geometrie van de constructie vanbelang; dynamische kenmerken als eigen frequenties van totaal en onderdelen spelen dus geenrol.Dan kan geschreven worden:vervalbelasting va = G (hw, bws, geometrie)golfbelastingsbeeld Sbb = H(hw, Snn, geometrie).De vervalbelasting is eenvoudig te bepalen door uit te gaan van hydrostatische drukverdelingenaan weerszijden van de kering alsmede een aangenomen drukverloop in de drempel. Omdat ersprake is van een nagenoeg lineair systeem kan, uitgaande van een golfspectrum, een golf-belastingsspectrum bepaald worden indien de overdrachtsfunctie bekend is:Sbb(f) = I0 (f) \2XSnn (f)f = golffrequentieDe overdrachtsfunctie 0 (f) wordt als volgt gedefinieerd: de golfbelasting (O-topwaarde) pereenheid van golfamplitude (meestal 1 meter), als functie van de golffrequentie, voor eengegeven hw. In figuur 7 is dit schematisch weergegeven.Evenals dit bij het golfspectrum het geval is, kan (bij voldoend smalle spectra, waarvan hiersprake iS) het spectrum worden gekarakteriseerd door de significante waarde G8z1/3 en degemiddelde periode Tz. De berekening hiervan is eenvoudig, namelijk met het Ode en 2demoment van het spectrum:flNHzf IN HzVARIABELESnnINM202 1N(kN/MFiguur 6SbbIN (kN~Figuur 7fiN Hzmn = Jfn X Sbb (f) df (2) enoG8z1/3 = 2vmo (3) (significante golfbelastingsamplitude)Tz = 2n' V! (4) (gemiddelde periode)De overdrachtsfuncties worden berekend op basis van de lineaire golftheorie die het mogelijkmaakt een golfdrukfiguur te bepalen afhankelijk van de reflectieco?ffici?nt (geometrie-afhankelijk) en de golfperiode en golfhoogte.De reflectieco?ffici?nten zijn bepaald met behulp van modelonderzoek in het WaterloopkundigLaboratorium te Delft, waar ook de toetsing van de berekende overdractitsfuncties heeft plaats-gevonden. Voor een gedetailleerde beschrijving wordt verwezen naar [4].De kansverdeling van de belastingenUithet voorgaande moge blijken dat het mogelijk is voor elke combinatie van hW,bws en Snn eengolfbelastingsspectrum Sbb en een vervalbelasting te bepalen, waarvan op grond van hetbehandelde in de paragraaf 'Natuurrandvoorwaarden' de kans bekend is, namelijk:kans (hWi,bwsj, VWk) = kans (V8 = V8ij en ~bb = Sik) (5)Als ontwerper is men niet ge?nteresseerd in een golfbelastingsspectrum, maar in een individuelegolfbelasting die samen met een vervalbelasting de totale belasting op de constructie geeft. Hierkomt het voordeel van de spectrale methode naar voren. Het blijkt mogelijk, analoog aan hetgolfspectrum zelf, de kansverdeling van de golfbelastingsamplituden te beschrijven met de zgn.Rayleigh-verdeling:kans (GB > TB} - kan nu worden gevonden als de somvan de gezamenlijke voorkomenskansen van VB en GB, waarvoor geldt.a x VB + f3 x GB > TBwaarin a en f3 gewichtsfactoren zijn die aangeven hoe zwaar de desbetreffende belasting-component meeweegt in de totaalbelasting.Voor de betonconstructie geldt: a = f3 = 1 (fig. 9).L MKans {TB> TB} = k k kans {VBI en GBm} x Z{= 1 m = 1waarin Z = 1 als a x V81 + f3 x GBm > TBen Z = 0 voor overige gevallen. Het resultaat is de kromme in figuur 10.De waarde van deze rekenpartij kan gemustreerd worden aan de hand van het volgende.Omstreeks 1976 was het nog zo, dat de ontwerpbelasting deterministisch was bepaald op grondvan de volgende natuurrandvoorwaarden:~:s : ~~~ ~ ~:~ ~} hieruit volgt vervalbelasting (VB)Hz1/3 = 4,5 m?~ Hindividueel = 2 Hz1/3 = 9 m } hieruit volgt golfbelasting (GB)T= 10sDe ontwerpbelasting kent als eis dat de overschrijdingskans ervan 2,5 x 10-4/jaaris. Nuiskans (hw > NAP + 5,5 m) = 2,5 x 10-4, terwijlkans (bws < NAP ~ 1,7 m) = 10-3 , zodat duidelijk is dat de vervalbelasting alleen al een over-schrijdingskans had van 10"6 ? 10-7. Deze werd vervolgens gecombineerd met ??n golfbelas-ting, waarvan nu bekend is dat de kans van overschrijden ook zeer klein is. Het is dan ook nietverwonderlijk, dat de met de probabilistische methode bepaalde ontwerpbelasting ca. 40%lager is dan de eerder gehanteerde deterministische ontwerpbelasting.DrukverdelingTen behoeve van het ontwerp moet deontwerper beschikken Over een ruimtelijke drukverdeling,op grond waarvan de constructie gedimensioneerd kan worden. Bij de stormvloedkering is hier-voor een deterministische keuze gedaan door terug te rekenen welke waterstand en golfspec-trumcombinatie de grootste bijdrage levert aan de overschrijdingskans van de ontwerpbe-lasting. Vervolgens is er een keuze gedaan met betrekking tot een individuele golf, die ge-zamenlijk met het verval, een belasting veroorzaakt gelijk aan de ontwerpbelasting.De natuurrandvoorwaarden worden in klassen opgedeeld, waardoor klassen ontstaan vanbuiten- en binnenwaterstanden. Per buitenwaterstandsklasse is er een verdeling van golf-belastingsspectra die op basis van de Rayleigh-verdeling omgezet kunnen worden in een grootaantal klassen van individuele golfbelastingen met bijbehorende kansen. Door elk van dehoogwaterstandsklassen, waarvan de voorkomenskans bekend is, nog te combineren metklassen van binnenwaterstanden waarvan eveneens de voorkomenskans bekend zijn, beschiktmen per combinatie van ??n hw- en bws-klasse (dus vervalklasse) over een kanshistogram vangolfbelastingen (fig. 8) ....... .::::.golfbelaslingklasse~GBYB. YBTB=a*YB +~G8:::: ::.LOG (kans(TJI-+TB)];g~~~~~~~g~.-~rval. O~veiligZ = ?~bezwijkenZ < ?~onveiligDe kans op falen is nu: p(F) = p(Z