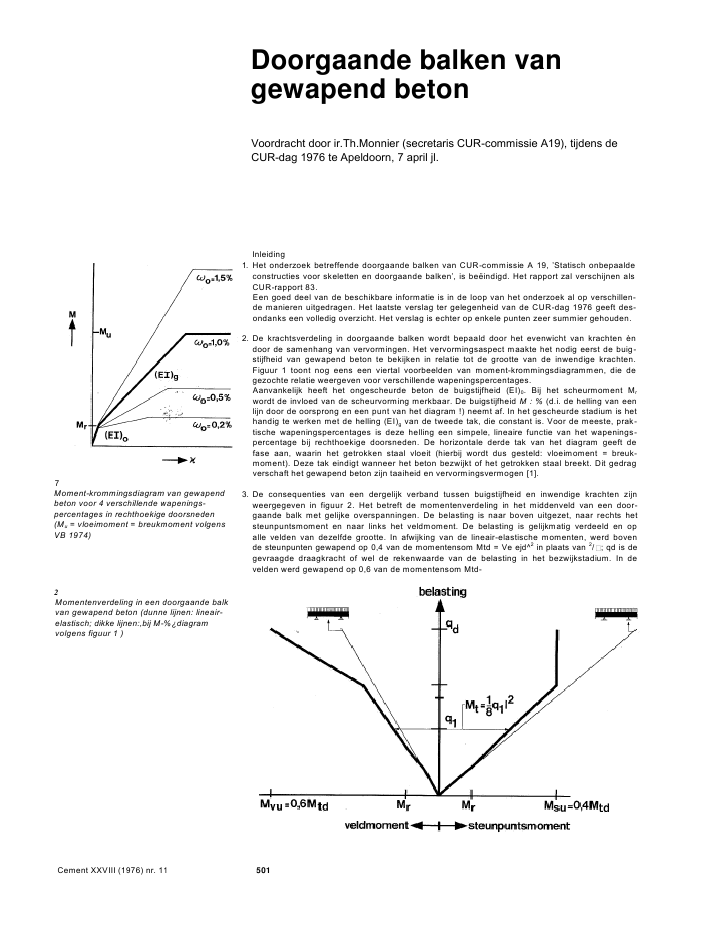
Doorgaande balken vangewapend betonVoordracht door ir.Th.Monnier (secretaris CUR-commissie A19), tijdens deCUR-dag 1976 te Apeldoorn, 7 april jl.7Moment-krommingsdiagram van gewapendbeton voor 4 verschillende wapenings-percentages in rechthoekige doorsneden(Mu = vloeimoment = breukmoment volgensVB 1974)Inleiding1. Het onderzoek betreffende doorgaande balken van CUR-commissie A 19, 'Statisch onbepaaldeconstructies voor skeletten en doorgaande balken', is be?indigd. Het rapport zal verschijnen alsCUR-rapport 83.Een goed deel van de beschikbare informatie is in de loop van het onderzoek al op verschillen-de manieren uitgedragen. Het laatste verslag ter gelegenheid van de CUR-dag 1976 geeft des-ondanks een volledig overzicht. Het verslag is echter op enkele punten zeer summier gehouden.2. De krachtsverdeling in doorgaande balken wordt bepaald door het evenwicht van krachten ?ndoor de samenhang van vervormingen. Het vervormingsaspect maakte het nodig eerst de buig-stijfheid van gewapend beton te bekijken in relatie tot de grootte van de inwendige krachten.Figuur 1 toont nog eens een viertal voorbeelden van moment-krommingsdiagrammen, die degezochte relatie weergeven voor verschillende wapeningspercentages.Aanvankelijk heeft het ongescheurde beton de buigstijfheid (EI)0. Bij het scheurmoment Mrwordt de invloed van de scheurvorming merkbaar. De buigstijfheid M : % (d.i. de helling van eenlijn door de oorsprong en een punt van het diagram !) neemt af. In het gescheurde stadium is hethandig te werken met de helling (EI)g van de tweede tak, die constant is. Voor de meeste, prak-tische wapeningspercentages is deze helling een simpele, lineaire functie van het wapenings-percentage bij rechthoekige doorsneden. De horizontale derde tak van het diagram geeft defase aan, waarin het getrokken staal vloeit (hierbij wordt dus gesteld: vloeimoment = breuk-moment). Deze tak eindigt wanneer het beton bezwijkt of het getrokken staal breekt. Dit gedragverschaft het gewapend beton zijn taaiheid en vervormingsvermogen [1].3. De consequenties van een dergelijk verband tussen buigstijfheid en inwendige krachten zijnweergegeven in figuur 2. Het betreft de momentenverdeling in het middenveld van een door-gaande balk met gelijke overspanningen. De belasting is naar boven uitgezet, naar rechts hetsteunpuntsmoment en naar links het veldmoment. De belasting is gelijkmatig verdeeld en opalle velden van dezelfde grootte. In afwijking van de lineair-elastische momenten, werd bovende steunpunten gewapend op 0,4 van de momentensom Mtd = Ve ejd^2in plaats van 2/ ; qd is degevraagde draagkracht of wel de rekenwaarde van de belasting in het bezwijkstadium. In develden werd gewapend op 0,6 van de momentensom Mtd-2Momentenverdeling in een doorgaande balkvan gewapend beton (dunne lijnen: lineair-elastisch; dikke lijnen:,bij M-%?diagramvolgens figuur 1 )Cement XXVIII (1976) nr. 11 501In de figuur geven de dunne lijnen de lineair-elastische momenten, dus berekend alsof de con-structie ongescheurd blijft. De dikke lijnen geven de momenten die werkelijk optreden, wanneerde belasting wordt aangebracht en verder toeneemt. Er treden afwijkingen op ten opzichte vande lineaire momenten wanneer scheurvorming ontstaat, de zogenaamde herverdeling van demomenten. Op grond van het vereiste evenwicht blijft de som van de veld- en steunpuntsmo-menten altijd Ve c/d^2. De herverdeling wordt belangrijk wanneer het betonstaal gaat vloeien;hier boven de steunpunten. Er ontstaat een plastisch scharnier waarin dank zij de mogelijk-heden uit het /--diagram over zekere lengte een rotatie optreedt, terwijl het vloeimoment Msugeleverd blijft worden. Verdere toename van de belasting komt nu uitsluitend voor rekening vande veldwapening. Dit gaat door tot ook in het veld het vloeimoment wordt gehaald. Stringentevoorwaarde is wel, dat g??n voortijdige breuk optreedt, dat wil zeggen dat de rotatiecapaciteitvoldoende is.Uit bovenstaande blijkt dat de totale wapening bepalend is voor de draagkracht. Daarbij is eenzekere vrijheid in de keuze van de wapeningsverdeling mogelijk.3Doorgaande balk na breuk4Momenten in een balk van gewapend beton:de stippen geven de gemeten waarden; dewapeningsverdeling komt overeen met delineair-elastische momentenverdelingExperimenteel onderzoek4. In het onderzoek zijn experimenten uitgevoerd om het een en ander te toetsen. Het betrofbalken op drie steunpunten, waarop vier puntlasten als belasting aangrepen (fig.3). De wape-ning werd gevarieerd ten opzichte van de wapening die nodig is met het oog op de lineair-elas-tische momenten [2].Figuur4 laateen van de resultaten zien. De stippen betreffen de geregistreerde momentenver-deling. De dunne lijn is de lineair-elastische momentenverdeling. De dikke lijn geeft aan welkemomentenverdeling theoretisch moet worden verwacht, uitgaande van het getoonde 3-takkigemoment-krommingsdiagram. De aangebrachte wapening was in dit geval afgestemd op delineair-elastische momentenverdeling. De gemeten momentenverdeling ligt dicht bij de lineair-elastische verdeling. Het steunpuntsmoment blijft enigszins achter bij wat theoretisch werd ver-wacht. Dit verschijnsel was ook bij de overige proefbalken aanwezig. De oorzaak moet wordengezocht bij de invloed van de dwarskracht op de buigstijfheid. Speciale aandacht verdient hetfeit, dat bij een wapening conform de lineair-elastische momentenverdeling, de optredendemomentenverdeling bij goede benadering ook inderdaad lineair elastisch is.Als volgend onderdeel van het onderzoek werd een rekenprogramma gemaakt. In dit reken-programma is voor de dwarskrachtinvloed op de stijfheid een elementair vastgestelde correctie-factor ingebouwd. Aldus konden de gemeten krachtsverdeling en de optredende vervormingengoed worden nagerekend. De simulatie van het gedrag van doorgaande balken met de compu-ter is ook getoetst aan een betrekkelijk groot aantal experimentele resultaten, dat in de literatuuris aangetroffen. De resultaten waren goed.Uitgaande van de desbetreffende moment-krommingsdiagrammen, wordt ook voor lange-duur-belasting en wisselende belasting de juiste momentenverdeling gevonden.Wat zijn nu de mogelijkheden van de vrijheid van wapenen?5. Doorgaans wordt in het bijzonder gedacht aan het verplaatsen van wapening van de steunpun-ten naar de velden. Dit staat in verband met de grote maatafwijkingen die soms in de ligging vande steunpuntswapening optreden. Een andere opvatting kan gelden met het oog op bij voor-beeld brand. Onder deze omstandigheden is de bovenliggende steunpuntswapening veel beterbeschermd en levert een betrouwbare bijdrage aan de brandwerendheid.Er is een zekere besparing van wapening mogelijk ten opzichte van het wapenen op extreme,lineaire momenten. Deze extreme momenten treden op bij verschillende belastinggevallen. Desom van de bijbehorende vloeimomenten wordt hierdoor groter dan de minimaal vereistewaarde Ve ml2- Er kan dus worden bezuinigd.De vrijheid van wapenen verschaft ook mogelijkheden voor standaardisatie. Dit is echter in hetalgemeen nog moeilijk te concretiseren. Bij beschouwingen over rationalisatie van wapeningkan enige vrijheid in de verdeling natuurlijk goed te pas komen.CUR-commissie A 19 heeft echter vooral gewerkt aan het verschaffen van methoden, waarmeede vrijheid van wapenen in de praktijk bruikbaar wordt. Het punt was daarbij niet zozeer hetbezwijkstadium, waarin voor de bepaling van de draagkracht een evenwichtsbeschouwing infeite al voldoende is. De voorwaarde voor de geldigheid van deze stelling is, dat voldoenderotatiecapaciteit aanwezig is. Daarvoor moeten de optredende rotaties en de rotatiecapaciteitdus aan elkaar worden getoetst. Bovendien moeten de gebruikseisen in het gebruiksstadiumworden gecontroleerd.Cement XXVIII (1976) nr. 11 5025Momentenverdeling in een doorgaande balkvan gewapend beton met een wapenings-verdeling volgens de lineair-elastischemomentenverdeling6Momentenverdeling in een balk vangewapend beton; boven de steunpunten isgewapend op 0,75 X het extreme, lineairemomentTabel 1Gemeten afwijkingen van de lineaire momen-ten in het gebruiksstadium bij proefbalken1) aanwezige breukmoment (volgens VB '74) /benodigde breukmoment van dezelfde door-snede van de balk met gelijke draagkracht,maar gewapend volgens de lineair-elastischemomentenverdeling2) in het gebruiksstadiumHet komt er op neer, dat over een groot gebied de momentenverdeling als functie van de belas-ting bekend moet zijn. Het probleem is, dat er g??n praktische methode bestaat waarmee dezesimpel kan worden vastgesteld. Er werd daarom gezocht naar een werkwijze, waarmee met ??nberekening naar de krachtsverdeling kan worden volstaan. Er zijn twee verschillende methodenontwikkeld.De lineair-elastische berekening met reductieregel6. De eerste methode gaat ervan uit dat de momentenverdeling in een doorgaande balk, die vooreen bepaald belastinggeval is gewapend op grond van de lineair-elastische momenten, bij datbelastinggeval ook een momentenverdeling vertoont conform de lineaire momenten (fig. 5).Bovendien kan worden vastgesteld dat een kleine variatie op die wapeningsverdeling g??ngrote verschillen oplevert in de gebruikstoestand (tabel 1). Een acceptabele variatie op delineaire momentenverdeling kan worden gesteld op 25%. In de VB 1974 is dit gesteld als eentoelaatbare reductie van ??n van de beide waarden die de momentensom bepalen.In figuur 6 is de momentenverdeling weergegeven van een middenveld van een doorgaandebalk met gelijke overspanningen onder een gelijkmatig verdeelde belasting. Twee belasting-gevallen zijn beschouwd:1. het geval volbelasting;2. het geval dat de velden afwisselend vol en voor 50% zijn belast.De dunne lijnen in de figuur geven de lineair-elastische verdelingen. Het extreme veldmomentbedraagt dan VuqF en het extreme steunpuntsmoment Vi2q?2die te zamen een som van debreukmomenten leveren van 7/48C?d^2.Cement XXVIII (1976) nr. 11 5037Theoretische rotatiecapaciteit bij recht-hoekige doorsneden8Moment-krommingsdiagram volgens deniet-lineaire elasticiteitstheorie van deVB 19749Momentenverdeling in een doorgaande balkvan gewapend beton (dunne lijnen: M-%-diagram van figuur 1; dikke lijnen:M-K-diagram van figuur 8)Voor de dimensionering van de wapening is echter gekozen voor een enigszins bijzonderewapeningsverdeling, waarbij de breukmomenten in de velden en ter plaatse van de steunpuntenalle gelijk zijn aan Vi6 Qd^2? Dit geeft de minimale momentensom Ve q