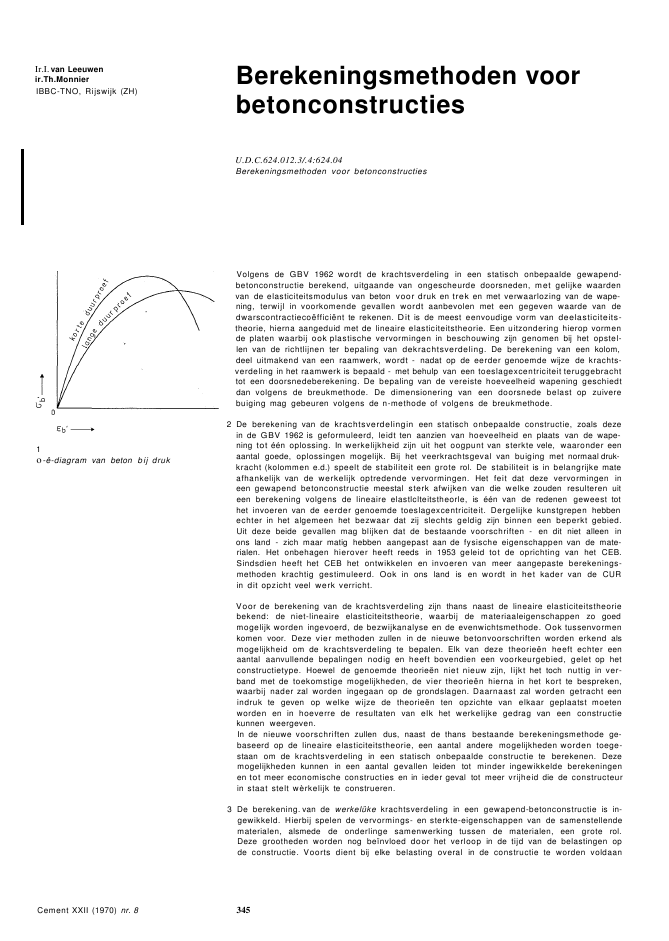
Ir.I. van Leeuwenir.Th.MonnierIBBC-TNO, Rijswijk (ZH)1o-?-diagram van beton bij drukCement XXII (1970) nr. 8Berekeningsmethoden voorbetonconstructiesU.D.C.624.012.3/.4:624.04Berekeningsmethoden voor betonconstructiesVolgens de GBV 1962 wordt de krachtsverdeling in een statisch onbepaalde gewapend-betonconstructie berekend, uitgaande van ongescheurde doorsneden, met gelijke waardenvan de elasticiteitsmodulus van beton voor druk en trek en met verwaarlozing van de wape-ning, terwijl in voorkomende gevallen wordt aanbevolen met een gegeven waarde van dedwarscontractieco?ffici?nt te rekenen. Dit is de meest eenvoudige vorm van deelasticiteits-theorie, hierna aangeduid met de lineaire elasticiteitstheorie. Een uitzondering hierop vormende platen waarbij ook plastische vervormingen in beschouwing zijn genomen bij het opstel-len van de richtlijnen ter bepaling van dekrachtsverdeling. De berekening van een kolom,deel uitmakend van een raamwerk, wordt - nadat op de eerder genoemde wijze de krachts-verdeling in het raamwerk is bepaald - met behulp van een toeslagexcentriciteit teruggebrachttot een doorsnedeberekening. De bepaling van de vereiste hoeveelheid wapening geschiedtdan volgens de breukmethode. De dimensionering van een doorsnede belast op zuiverebuiging mag gebeuren volgens de n-methode of volgens de breukmethode.2 De berekening van de krachtsverdelingin een statisch onbepaalde constructie, zoals dezein de GBV 1962 is geformuleerd, leidt ten aanzien van hoeveelheid en plaats van de wape-ning tot ??n oplossing. In werkelijkheid zijn uit het oogpunt van sterkte vele, waaronder eenaantal goede, oplossingen mogelijk. Bij het veerkrachtsgeval van buiging met normaal druk-kracht (kolommen e.d.) speelt de stabiliteit een grote rol. De stabiliteit is in belangrijke mateafhankelijk van de werkelijk optredende vervormingen. Het feit dat deze vervormingen ineen gewapend betonconstructie meestal sterk afwijken van die welke zouden resulteren uiteen berekening volgens de lineaire elastlclteitstheorle, is ??n van de redenen geweest tothet invoeren van de eerder genoemde toeslagexcentriciteit. Dergelijke kunstgrepen hebbenechter in het algemeen het bezwaar dat zij slechts geldig zijn binnen een beperkt gebied.Uit deze beide gevallen mag blijken dat de bestaande voorschriften - en dit niet alleen inons land - zich maar matig hebben aangepast aan de fysische eigenschappen van de mate-rialen. Het onbehagen hierover heeft reeds in 1953 geleid tot de oprichting van het CEB.Sindsdien heeft het CEB het ontwikkelen en invoeren van meer aangepaste berekenings-methoden krachtig gestimuleerd. Ook in ons land is en wordt in het kader van de CURin dit opzicht veel werk verricht.Voor de berekening van de krachtsverdeling zijn thans naast de lineaire elasticiteitstheoriebekend: de niet-lineaire elasticiteitstheorie, waarbij de materiaaleigenschappen zo goedmogelijk worden ingevoerd, de bezwijkanalyse en de evenwichtsmethode. Ook tussenvormenkomen voor. Deze vier methoden zullen in de nieuwe betonvoorschriften worden erkend alsmogelijkheid om de krachtsverdeling te bepalen. Elk van deze theorie?n heeft echter eenaantal aanvullende bepalingen nodig en heeft bovendien een voorkeurgebied, gelet op hetconstructietype. Hoewel de genoemde theorie?n niet nieuw zijn, lijkt het toch nuttig in ver-band met de toekomstige mogelijkheden, de vier theorie?n hierna in het kort te bespreken,waarbij nader zal worden ingegaan op de grondslagen. Daarnaast zal worden getracht eenindruk te geven op welke wijze de theorie?n ten opzichte van elkaar geplaatst moetenworden en in hoeverre de resultaten van elk het werkelijke gedrag van een constructiekunnen weergeven.In de nieuwe voorschriften zullen dus, naast de thans bestaande berekeningsmethode ge-baseerd op de lineaire elasticiteitstheorie, een aantal andere mogelijkheden worden toege-staan om de krachtsverdeling in een statisch onbepaalde constructie te berekenen. Dezemogelijkheden kunnen in een aantal gevallen leiden tot minder ingewikkelde berekeningenen tot meer economische constructies en in ieder geval tot meer vrijheid die de constructeurin staat stelt w?rkelijk te construeren.3 De berekening. van de werkel?ke krachtsverdeling in een gewapend-betonconstructie is in-gewikkeld. Hierbij spelen de vervormings- en sterkte-eigenschappen van de samenstellendematerialen, alsmede de onderlinge samenwerking tussen de materialen, een grote rol.Deze grootheden worden nog be?nvloed door het verloop in de tijd van de belastingen opde constructie. Voorts dient bij elke belasting overal in de constructie te worden voldaan3452Invloed van wisselende belastingop o3o van staalHW= warmgewalstHK = koud vervormdVoor de berekening van de krachtsverdeling in een statisch onbepaalde betonconstructie,alsmede voor de berekening van constructiedelen waarbij de stabiliteit een rol speelt, ishet M-N-x-diagram een belangrijk hulpmiddel. In dit diagram wordt voor een gegevendwarsdoorsnede van bijv. een balk, kolom, plaat, wand, stijve kern en dergelijke het verbandweergegeven tussen het buigend moment M en de bijbehorende kromming en wel vooreen gegeven constante normaalkracht N (fig. 4). In deze figuur is dit verband schematischweergegeven voor verschillend grote waarden van N. Voorts is in de figuur aangenomendat het buigend moment ??nmalig wordt opgevoerd tot bezwijken van de doorsnede op-treedt. Het blijkt dat het verband tussen M en sterk afhankelijk is van de grootte van N.Het verloop vertoont knikpunten waar bijv. het beton scheurt of het staal de vloei- of stuik-grens bereikt. Voor het geval dat N = 0 (buiging zonder normaalkracht) wordt hetMdiagram verkregen. De buigstijfheid is gelijk aan de verhouding De grootte van de buig-stijfheid is dus zowel afhankelijk van de grootte van M als van N, Het M-N-x-diagram isniet alleen afhankelijk van de vorm en afmetingen van de dwarsdoorsnede, inclusief dehoeveelheid en de plaats van de wapening, maar ook van de van het betonHet van het staal wordt ontleend aan een trekproef. Voor druk wordthetzelfde verband aangehouden. De opgaande tak van het diagram (fig. 3) is recht en, ondernormale omstandigheden, niet afhankelijk van de belastingshistorie. Het volgende gedeeltewordt, afhankelijk van de etaalkwalltelt, al dan niet ingeleid door een vloeitraject. Wordtna het bereiken van dit gedeelte de belasting weggenomen, dan ontstaat een blijvendevervorming (fig. 3).De onderlinge samenwerking tussen staal en beton betekent voor het veerkrachtsgeval vanbuiging met of zonder normaalkracht dat het staal ten opzichte van het beton niet magverschuiven. In het algemeen kan worden gesteld dat deze samenwerking bij toepassingvan goed geprofileerd staal is gewaarborgd. Ten aanzien van glad staal zal deze waarborgveelal verkregen moeten worden uit de toepassing van haken of andere voorzieningen.aan de eisen die het statisch evenwicht stelt, terwijl tevens de samenhang tussen opvolgen-de doorsneden gewaarborgd dient te zijn.De kennis omtrent het gedrag van beton onder invloed van een belasting beperkt zich inhoofdzaak tot de kennis verkregen uit proeven, waarbij in de lengterichting van een proef-stuk, dat meestal de vorm van een prisma of cilinder heeft, een drukkracht wordt aange-bracht. Tijdens het opvoeren van de belasting wordt de verkorting van het materiaal ge-meten. Dit leidt tot een c-s-dlaqrarn - zoals schematisch in fig. 1 is aangegeven- dat hetgedrag van beton dus weergeeft onder invloed van een ??n-assige, c.q, lijnspanningstoe-stand. De maximaal bereikte spanning wordt de sterkte genoemd. De vorm van het diagramblijkt onder meer afhankelijk te zijn van de belastingsnelheid (fig. 1), van de betonkwaliteiten van de vorm en afmetingen van het proefstuk. Bij het wegnemen van de belasting tredenvoorts nog blijvende vervormingen op zoals fig. 2 laat zien. Het op dezelfde wijze bepalenvan het bij een ??n-assige trekbelasting blijkt niet zo eenvoudig te zijn, ondermeer omdat door het krimpen van het proefstuk initi?le trekspanningen ontstaan, die hetresultaat belangrijk kunnen be?nvloeden, vooral ten aanzien van de sterkte. Hoewel in ver-schillende laboratoria in binnen- en buitenland momenteel onderzoekingen gaande zijn metbetrekking tot het gedrag van beton onder invloed van een meer-assige spanningstoestand,moet de huidige kennis hieromtrent als summier worden gekenschetst. De theorie?n terbepaling van de krachtsverdeling in een betonconstructie zullen zich om deze reden voor-lopig moeten beperken tot de veerkrachtsgevallen, waarbij een lijnspanningstoestand op-treedt, te weten buiging met of zonder normaalkracht. Veerkrachtsgevallen zoals dwars-kracht, pons en wringing zullen dus niet in beschouwing worden genomen. Daarentegenzullen platen w?l worden beschouwd, ofschoon in deze constructiedelen eveneens eenmeer-assige spanningstoestand optreedt. Bij platen wordt echter aangenomen dat de op-tredende hoofdmomenten onafhankelijk van elkaar kunnen worden beschouwd.IIIIIIIIIIIIIIIIIIIIIiIIIIi/Ii'/ bgtg Eoo 0,2'I,,0N=04aM-N-x-diagrammen van een gegevendoorsnede (N4) N3 > N2 > Nl)Mii4bMDefinitie van en van de buigstijfheidCement XXII (1970) nr. 8 3464 HetIljkt dus weinig zinvol te trachten het toekomstige gedrag van een constructie doormiddel van een berekening exact te voorspellen. Om deze reden verdient het de voorkeurde aandacht te richten op meer praktische berekeningsmethoden, waaraan w?l de eis moetworden gesteld dat zij in voldoende mate waarborgen dat gedurende de gehele levensduurvan de constructie aan de eis inzake veiligheid tegen bezwijken en aan bruikbaarheidseisenwordt voldaan. Alvorens op deze berekeningsmethoden nader in te gaan is het noodzakelljkna te gaan op welke wijze een statisch onbepaalde constructie zich gedraagt onder invloedvan een toenemende belasting.Bij een geringe belasting zal de constructie nergens gescheurd zljn, aannemende dat geenscheuren zijn opgetreden door krimp of door momenten ten gevolge van het eigen gewicht.De buigstijfheid wordt dan bepaald door ongescheurde doorsneden, waarbij de invloed vande wapening kan worden verwaarloosd. Ook de aanwezigheid van een eventuele normaal-kracht speelt geen grote rol. De krachtsverdeling zal zich aanpassen aan de onderlingebuigst[jfheidsverhouding. Na verhoging van de belasting zal ten gevolge van scheurvormingde buigstijfheidsverhouding veranderen en daarmede dekrachtsverdeling. De buigst[jfheidwordt in gebieden waar scheurvorming optreedt in grote mate afhankeljjk van de aldaaraanwezige wapening en van de grootte van een eventuele normaalkracht. Gedeelten metveel wapening zijn relatief stijver en zullen dus moment aantrekken (fig. 6).In een constructie waarin alleen buiging zonder normaalkracht optreedt, ontwikkelt zich bijvoortgaande verhoging van de belasting een bezw[jkmechanisme, doordat op plaatsen waarhet staal de (conventionele) vloeigrens bereikt het moment niet of nauwelijks meer toe-neemt, maar de kromming daarentegen snel groter wordt (zie fig. 4 voor N = 0). Hieruitvolgt dat op deze plaatsen een relatief grote hoekverdraaiing (rotatie) optreedt, waardoorzgn. vloeischarnieren ontstaan. Bi] voortgezette verhoging van de belasting gedragen dezeplaatsen zich inderdaad als scharnieren, echter met een ongeveer gelijk blijvend moment.enen mindere mateloopt hetvan een langeduur-belasting op hetwel verdere onderzoekingen op dit gebied gewenstwisselend moment als een wisselende normaalkrachtviaduct of van een kraanbaan) is niets bekend.Het eindpunt van een (zie x in fig. 4) wordt bereikt doordat het beton ver-bnjzelt dan wel doordat het staal breekt. Dit eindpunt geeft dus de sterkte van de door-snede weer. Uit fig. 4 blijkt dat in geval N = 0 (buiging zonder normaalkracht) v??r die tijdeen groot wordt doorlopen bi] een ongeveer gelijkblijvend moment ten gevolgevan de relatief grote vervorming die het staal kan ondergaan (fig. 3). Zoals hierna zalbl[jkenwordt bij de bezwijkanalyse van deze eigenschap gebruik gemaakt.Uit het blijkt dus dat de buigst[jfheid zowel afhankelijk is van de dwars-doorsnede, inclusief de wapening, als van dekrachtsverdeling. (SU een ontwerpberekeningzijn de twee laatste echter juist de onbekenden.) Eerst dienen dus alle afmetingen vaneen statisch onbepaalde constructie te worden aangenomen, inclusief die van de wapening,waarna vervolgens geconcludeerd kan worden of de gekozen afmetingen leiden tot eenoplossing waarbij aan de eisen ten aanzien van de veiligheid tegen bezwijken is voldaanalsmede aan andere bruikbaarheidseisen, zoals scheurvorming en doorbuiging. Is dit niethet geval dan zal de berekening moeten worden herhaald met gewijzigde wapening. Ditis dus een iteratieproces dat tot ingewikkelde berekeningen leidt. Dit maakt in het alge-meen het gebruik van computerprogramma's noodzakelijk. Het voordeel is uiteraard wel dathet gedrag van de constructie van de onbelaste toestand tot aan het bezwijken rekenender-wijs kan worden gevolgd. Ook op deze wUze is echter een volledige voorspelling van hetgedrag niet mogel[jk, omdat de toekomstige belastingen niet voldoende nauwkeurig bekendzijn en dus evenmin de invloed van het verloop van de belastingen op hetc.q. de bulqatljfheid. Voorts is de treksterkte van beton een minder betrouwbaar gegeven.Wordt de treksterkte in de berekening verwaarloosd, maar is deze in werkelijkheld w?laanwezig, dan kan een groot verschil optreden tussen het door de berekening voorspeldeen het werkelijke gedrag van de constructie.18psteunpuntpp6bVoorbeeld van een bezweken ligger op driesteunpunten6aVoorbeeld van een veranderende krachts-verdeling bij toenemende belasting bij eenligger op drie steunpuntenMs = scheurmomentvolgens Iin. el.-theorieMus = vloeimoment t.p.v. steunpunt---- werkelijke momentenverdelingMuv = vloeimoment t.o,v, veld5Voorbeeld van een in gevalvan een wisselend (positief - negatief)momentCement XXII (1970) nr. 8 347Het constructietype bepaalt het aantal vloeischarnieren dat nodig is om een bezwijkmecha-nisme te vormen; is dit gevormd dan zakt de gehele constructie in elkaar bij gelijkblijvendebelasting.In een constructie waarbij in een aantal constructiedelen buiging met normaalkracht op-treedt,is de mogelijkheid tot vorming van vloeischarnieren in deze delen veel geringer (ziefig. 4, N =/= 0), omdat de aanwezigheid van de normaalkracht de maximale kromming doetafnemen. De mogelijkheid tot aanpassing van de krachtsverdeling is in een dergelijke con-structie in het bezwijkstadium dan ook geringer dan in de eerderbesproken constructie.Bovendien kan, alvorens de maximale kromming wordt bereikt, een dergelijk constructiedeelinstabiel worden, dat wil zeggen dat een geringe verhoging van de belasting de uitbuigingvan het constructiedeel onbepaald doet toenemen.In het gedrag van een constructie kunnen dus afhankelijk van de grootte van de belastingdrie stadia worden onderscheiden nl. het ongescheurde stadium, het gescheurde stadiumen hetbezwijkstadium. Terugkerend naar de praktische berekeningsmethoden kan wordengesteld dat daarmee wordt getracht met vereenvoudigde grondslagen de krachtsverdelingin ??n of twee van de drie genoemde stadia vast te stellen. De rekenmethoden moeten dusworden gezien als zo goed mogelijke benaderingen van het werkelijke gedrag van de con-structie inde betreffende stadia. In alle gevallen wordt echter, uitgaande van de aldusberekende krachtsverdeling, de vereiste hoeveelheid wapening bepaald met behulp van eendoorsnedeberekening die wordt betrokken op het bezwijkstadium. Ten einde, ongeacht detoegepaste rekenmethode, deze werkwijze steeds mogelijk te maken, alsmede om de con-structie steeds aan bruikbaarheidseisen te kunnen toetsen, zijn bij de verschillende reken-methoden aanvullende bepalingen noodzakelijk die corrigerend werken.Achtereenvolgens zullen nu worden besproken de vier methoden die in het begin van ditartikel reeds zijn vermeld. De grondslagen van de doorsnedeberekeningkomen overeen metdie van de niet-lineaire elastlclteitstheorle en zullen aldaar worden uiteengezet.5 In de nieuwe betonvoorschriften zullen zowel de lineaire elasticiteitstheorie als de niet-lineaire elastlclteitstheorte worden opgenomen. In de zin van de voorschriften betekentelastisch dat voor elk elementje van de constructie het verband tussen de inwendige krach-ten en de bijbehorende vervormingen bij belasten volkomen gelijk is aan dat bij ontlasten.Het woord elastisch zegt evenwel niets over de vorm van dit verband; deze vorm kan inprincipe geheel willekeurig zijn. Is het verband rechtlijnig, dan wordt gesproken over lineairelastisch; in alle andere gevallen over niet-lineair elastisch (fig. 7).7Definitie van lineair elastisch en niet-lineairelastischcE0?._ .ve r vor m i nq c-c.s vervo r m rneo i r el as t isc h niet elastischCement XXII (1970) nr. 85a De lineaire elasticiteitstheorieBij deze theorie dient te worden voldaan aan de eisen die het statisch evenwicht stelt, als-mede aan de voorwaarde van samenhang tussen opvolgende doorsneden. Uitgegaan wordtvan ongescheurd beton, waarbij voor druk en trek dezelfde waarde van de elasticiteits-modulus geldt. De wapening mag bij de bepaling van de stijfheid worden verwaarloosd.Deze uitgangspunten leiden tot een M-x-diagram waarvan de vorm overeenkomt met hetlineair-elastische diagram van fig. 7. Ook de invloed van een normaalkracht op de buig-stijfheid wordt verwaarloosd. De invloed van kruip bij een langdurige belasting kan in reke-ning worden gebracht door invoering van een kruipmaat, waardoor de waarde van deelasticiteitsmodulus kleiner wordt.De dwarscontractieco?ffici?nt mag gelijk aan nul worden gesteld, desgewenst kan eenwaarde worden ingevoerd.Op grond van deze onderstellingen worden dus scheurvorming, plaatselijk vloeien van dewapening en de hieruit voortvloeiende wijzigingen in de krachtsverdeling buiten beschouwinggelaten. De theorie mag alleen worden gebruikt voor de bepaling van de krachtsverdelingen niet voor de dimensionering van doorsneden. Er wordt op gewezen dat het verbandtussen uitwendige krachten en de vervormingen (in tegenstelling tot dat tussen de inwendigekrachten en de vervormingen) ook bij deze theorie in principe niet lineair behoeft te zijn,zoals in die gevallen waar de uitbuiging van een constructiedeel van invloed is op dekrachtsverdeling (kolommen e.d.).De theorie, die overeenkomt met de methode opgenomen in de GBV 1962, leidt dus in feitealleen tot een goede benadering van de krachtsverdeling bij een geringe belasting, waarbijnog geen scheurvorming is opgetreden. Het aantrekkelijke van de methode is dat na het348vaststellen van de betonafmetingen de krachtsverdeling kan worden bepaald en daarna dehoeveelheid wapening. Het is dus een ontwerpberekening. Voorts wordt in handboekenvoor vele constructietypen de krachtsverdeling gegeven. Bovendien is in alle gevallen,waarin het verband tussen de uitwendige krachten en de optredende vervormingenrechtlijnig is, het superpositiebeginsel geldig, zodat gaapvergelijkingen, methode Cross e.d.,kunnen worden toegepast. Het bezwaar is echter dat, afgezien van enige invloed van dedwarscontractieco?ffici?nt in sommige gevallen, de methode slechts leidt tot ??n oplossing,terwijl andere, goede oplossingen ook mogelijk zijn.Zoals eerder vermeld, worden de wijzigingen in de krachtsverdeling ten gevolge van scheur-vorming e.d. buiten beschouwing gelaten. Bij een constructie, waarbij alleen buiging zondernormaalkracht. optreedt, zal inderdaad de krachtsverdeling na volledige ontwikkeling van descheurvorming ongeveer dezelfde en in het bezwijkstadium precies dezelfde zijn als die inhet ongescheurde stadium. Dit is een gevolg van de evenredigheid die bestaat tussen debuigstijfheid in het gescheurde stadium, de hoeveelheid wapening en de optredende mo-menten in het ongescheurde stadium. De grootste afwijking van deze krachtsverdeling treedtop na de eerste scheurvorming; bij opvoering van de belasting neemt deze afwijking weer af.Bij een constructie echter waarin buiging met normaalkracht optreedt, waarbij geen lineairverband bestaat tussen de uitwendige krachten en de optredende vervormingen (kolommene.d.), kunnen na scheurvorming grote afwijkingen in de krachtsverdeling optreden ten op-zichte van die in het ongescheurde stadium, Ten aanzien van dit veerkrachtsgeval geeft delineaire elasticiteitstheorie dan ook geen bevredigende oplossing. In de nieuwe voorschriftenwordt, evenals in de GBV 1962, onder meer om deze reden voor de berekening van kolom-men een toeslagexcentriciteit ingevoerd. Deze zal echter gedifferentieerder zijn dan die inde GBV 1962. Een dergelijke bepaling blijft uiteraard een kunstgreep en de toeslagexcen-triciteit heeft dan ook in het algemeen geen fysische betekenis.De dimensionering aan de hand van een doorsnedeberekening moet voor buiging met ofzonder normaalkracht worden uitgevoerd volgens de onderstellingen en met degrammen van het staal en beton, zoals deze in Sb zullen worden aangegeven.De eis ten aanzien van de doorbuiging wordt in eerste instantie betrokken op het gescheur-de stadium. De uit de lineair elastische berekening voortvloeiende doorbuiging zal dusgecorrigeerd moeten worden met een factor die onder meer afhankelijk is van de verhoudingtussen de buigstijfheid van de ongescheurde en de gescheurde doorsnede. In de nieuwevoorschriften zullen hiervoor bepalingen worden opgenomen.De controle van de maximale scheurwijdte is een aparte berekening. De staalspanningin het stadium waarin de scheurwijdte moet worden getoetst en die in de onderhavigescheurwijdteformule moet worden ingevoerd, kan worden gevonden door uit te gaan van deonderstelling dat deze lineair samenhangt met het in dat stadium optredende momentzodat:= Mu?Hierin stelt Mu het vloeimoment breukmoment) voor en de vloeigrens van het staal.8van staal voor gewapend beton ?volgens de nieuwe voorschriften(Eo = 2,1 . 106kgf/cm2)kgf Icm2iSb De niet-lineaire elasticiteitstheorieBij deze theorie wordt uitgegaan van de volgende onderstellingen:het beton kan geen trekspanningen opnemen;de verleogingen en verkortingen die de vezels door buiging ondergaan zijn rechtevenredigmet de afstand tot de neutrale lijn;het van het staal en het beton moeten worden aangenomen zoals hierna zalworden besproken.Met deze onderstellingen kan voor een gegeven dwarsdoorsnede een wor-den bepaald waarmede de buigstijfheid is vastgelegd. Desgewenst kan op dezelfde wijzede rekstijfheid door middel van een N-M-Ez-diagram worden bepaald. Onder de rekstijfheidwordt verstaan de stijfheid tegen de verlenging, c.q. verkorting ter plaatse van hetzwaartepunt van de doorsnede.Met behulp van deze diagrammen en rekening houdend met de eisen die het statisch even-wicht stelt, alsmede met de voorwaarde van samenhang tussen opvolgende doorsneden,kan de vervormingstoestand en de krachtsverdeling in een statisch onbepaalde constructieten gevolge van een gegeven belasting worden bepaald. Zoals onder 3 reeds is geschetstzal een dergelijke berekening in het algemeen met een computer moeten worden uitge-voerd *). Daar de M-N-X-diagrammen mede afhankelijk zijn van de afmetingen van de door-snede, inclusief de wapening, zullen deze eerst dienen te worden vastgesteld alvorens kanworden gerekend. De methode is dus in feite een controleberekening. Met deze methodewordt getracht het werkelijke gedrag vaneen constructie zowel in het gescheurde als in hetbezwijkstadium zo goed mogelijk te benaderen.*)Het is mogelijk om bij computerberekeningendirect met de te werkenen dus de M-N-x-diagrammen als tussen-fase te elimineren.Cement XXII (1970) nr. 8Door die belasting aan te brengen op de constructie, waarbij aan eisen van scheurvormingof doorbuiging moet worden voldaan, kan de gehele constructie rekenenderwijs aan dezeeisen worden getoetst. Evenzo kan, na het aanbrengen van die belasting die de constructiein het bezwijkstadium nog juist moet kunnen weerstaan, deze constructie overal worden ge-toetst aan de eis inzake de veiligheid tegen bezwijken. Dit bezwijken kan optreden ?f omdatin een doorsnede het eindpunt van het M-N-x-diagram wordt bereikt (zie x in fig. 4) ?fdoor instabiliteit van bijv. een kolom.34911Reductie van o-e-dteqrem i.v.m. spreidingin de sterkte10Vorming van het bi-lineair diagram(streeplijn)=bg tg Eo =helling raaklijn in 0 aangemiddeld=bg tg (0,9 Eo) =helling opgaande takvan bi-lineair diagram)Hieruit mag blijken dat uit de berekening zowel de krachtsverdeling in het bezwllkstadtumals de sterkte van de constructie volgt. De grondslagen voor de dimensionering door middelvan een doorsnedeberekening z!jn dus gel(jk aan die voor de bepaling van de krachts-verdeling. Voor beide gevallen worden deze vastgelegd in het Het zaloverigens duldelijk zijn dat, gezien de vorm van het het superpositiebe-ginsel niet geldt. Wanneer uit de berekening blijkt dat aan ??n van de eisen niet wordtvoldaan, zal de berekening moeten worden herhaald met gewUzigde wapening.Behalve het feit dat deze methode een zo goed mogel(jke benadering geeft van het werkelljkgedrag van deconstructie in het gescheurde en in het bezwijkstadium, is hetaantrekkel?kedat deze kan leiden tot meerdere goede oplossingen, zodat de constructeur de vrijheidheeft de zijns inziens meest gewenste oplossing te kiezen. Voorts mag uit het voorgaandeblUken dat geen afzonderlijke berekeningen nodig zUn ten aanzien van stabiliteit en door-bUiging,. terwUI de in de scheurw(jdteformule in te voeren staalspanning eveneens directwordt verkregen.In de nieuwe betonvoorschriften wordt voor alle staalsoorten het bilineaire o-s-dlaqram,zoals weergegeven in fig. 8, verplicht gesteld. De maximale in rekening te brengen ver-lenging wordt dus beperkt tot 30%0. De maximale drukspanning is gelUk aan de stuikgrense'e echter met de beperking dat deze spanning niet groter mag worden aangenomen dan4200 kgfjcm2, zijnde de spanning die behoort bij een verkorting van 2%0. In nader tebepalen gevallen mag echter voor koudvervormde staalsoorten een meer aangepast diagramworden gebruikt.Voor het beton zal eveneens een bilineair c-e-diaqram worden voorgeschreven, zoals infig. 9 is weergegeven. De helling van de opgaande tak wordt bepaald door de grootte vande elasticiteitsmodulus E, die afhankelijkIs van Eo en dekruipmaat De grootte van Eowordt bepaald uit de helling in de oorsprong van het c-e-draqram dat na 28 dagen verhar-ding wordt verkregen aan de hand van een drukproef op een prisma of cilinder. Zowel voorEo als voor zullen bepalingen in de voorschriften worden opgenomen. De ligging van dehorizontale tak wordt bepaald door de rekenwaarde van de sterkte b", Deze waarde zalbij aanwezigheid vaneen uitwendige normaaldrukkracht lager zUn dan bU buiging zondernormaalkracht. De maximale verkorting wordt, evenals in de GBV 1962, aangehouden op3,50/00. Bij toepassing van de niet-lineaire elastlclteltstheorle kan de constructeur aan dehand van de gegeven bepalingen voor ieder geval het best aangepaste diagram vaststellen.Dit diagram zal in het ene geval meer tot een rechthoek naderen en in andere geval meertot een driehoek. Daar de niet-lineaire elasticiteitstheorie in het algemeen met behulp vaneen computer zal worden toegepast lUkt dit geen bezwaar. SU toepassing van de lineaireelasticiteitstheorie, de bezwjjkanalyse of de evenwichtsmethode zal voor de dimensioneringvan de doorsnede een standaard diagram worden voorgeschreven, zodanig dat het resultaatweinig of niet zal afwijken van dat verkregen met de tweedegraadsparabool van de GBV1962.Het is voorts mogel!jk veilig te schematiseren. Deze schematiseringmoet dan zodanig zijn dat bl] iedere combinatie van M en N de bljbehorende niet kleineris dan volgens de diagrammen het geval zou z!jn. Deze benadering moet dan wel consequentin de gehele constructie worden. doorgevoerd.In het kort zUn de overwegingen die tot de keus van het bilineair diagram hebben geleidals volgt samen te vatten:Wanneer van een hoeveelheid beton een aantal croS-diagrammen wordt bepaald op deeerder beschreven wUze, dan zullen deze diagrammen onderling spreiding vertonen, zodatzich een bundel IUnen vormt wanneer de diagrammen t.o.v. dezelfde co?rdinaatassen wordenuitgezet (fig. 10). In de figuur is schematisch het gebied aangegeven waarbinnen 90% vanalle waarnemingen is gelegen alsmede het gemiddelde diagram.3,5 'lkorokteristiekep r ! s rn c ruksterktevoor b ui ?l n ? zondernormaalkracht)5% grens?e midde I depr l 5 rnu.d ruk sterkte'pbeton volgens de nieuwelo9vanvoorschriftenE = 0,9 Eo1 +?Door de ontwikkeling in de bouw in ons land zullen stabiliteitsberekeningen steeds belang-rijker worden. Bij een derqelilke berekening speelt de uitbuiging van een constructiedeeldat op buiging met normaaldrukkracht wordt belast een grote rol en daarmede ook de stijf-heid. Deze uitbuiging wordt bepaald door het gehele constructiedeel, d.W.Z. door alle op-eenvolgende doorsneden. Een plaatselijk kleinere stijfheid zal de uitbuiging nauwelijksbe?nvloeden. Het constructiedeelzal bezwijken in de maatgevende doorsnede. De draag-kracht hangt dus af van de plaatselijke materiaalsterkte in deze doorsnede en van degemiddelde stijfheid van het gehele constructiedeel. De in een berekening in te voerensterkte moet dus worden betrokken op een ondergrens; de stijfheid echter op eengemiddelde waarde van de E-modulus. Bij de tweedegraadsparabool in de GBV 1962 is dereductie in de sterkte daarentegen op dezelfde wijze doorgevoerd ten aanzien van deE-modulus (fig. 11). In fig. 10 is aangegeven dat de horizontale tak van het bilineaire dia-gram correspondeert met een ondergrens van de sterkte, terwijl de helling van de opgaandetak zo goed mogelijk overeenkomt met het verloop van het gemiddeld c-s-dlaqram. Tenslotte kunnen langeduureffecten op de sterkte en op de E-modulus afzonderlijk in rekeningworden gebracht. De grootte van de E-modulus is dus een re?le waarde en geldt voor allestadia. Voorts is het diagram eenvoudig van vorm zodat geen behoefte meer bestaat aaneen vereenvoudigd (rechthoekig) diagram zoals in de GSV 1962 is opgenomen voor deberekening van ingewikkelde doorsneden.Cement XXl! (1970) nr. 8 350Sc De elementaire bezwijkanalyse en de vloeilijnentheorieZoals de naam reeds aangeeft heeft deze theorie betrekking op het bezwijkstadium. Deconstructie wordt in dit stadium geschematiseerd tot een mechanisme bestaande uit on-vervormde delen die onderling en aan de ondersteuningen zijn verbonden door scharnieren.Deze scharnieren kunnen zijn vloeischarnieren (liggers), vloeilijnen (platen) of scharnierendeopleggingen. In geval van staafvormige constructies wordt gesproken over elementairebezwijkanalyse; in geval van platen over vloeilijnentheorie. De constructie zakt onder gelijk-blijvende belasting in elkaar zodra zich voldoende scharnieren hebben gevormd.Het woord 'elementair' heeft betrekking op het in de berekening verwaarlozen van allevervormingen ten opzichte van die in de scharnieren. Het uit fig. 4 wordt dusop de in fig. 12 aangegeven wijze. De verticale tak heeft betrekking op deonvervormde delen, de horizontale tak op de vloeischarnieren. Met de elementaire bezwijk-analyse kunnen om deze reden geen stabiliteitsberekeningen worden uitgevoerd.Uiteraard dienen zodanig plastische vervormingen te kunnen optreden dat inderdaad vloei-scharnieren ontstaan met voldoende rotatiecapaciteit (= hoekverdraaiingscapaciteit, ziefig. 13).De hoekverdraaiing is gelijk aan het produkt van de kromming en de lengte van hettraject waarover deze kromming aanwezig is. De vorm. van het vertoont dusgrote overeenkomst met die van het In fig. 4 is reeds gebleken dat de aan-wezigheid van een normaaldrukkracht de maximale kromming en daarmede doetafnemen. De elementaire bezwijkanalyse wordt dan ook voorlopig beperkt tot het geval vanbuiging zonder normaalkracht. Echter ook in het laatste geval zal een beperking moetenI worden opgelegd en wel aan de maximale hoeveelheid wapening in een doorsnede. HetI wapeningspercentage moet steeds zodanig zijn dat alvorens in een op buiging belastedoorsnede het beton bezwijkt, het staal reeds een zeker vloeitraject heeft doorlopen. Naar-mate het percentage groter wordt zal dit traject afnemen en daarmede resp. HetI kan zover worden opgevoerd dat in de doorsnede gelijktijdig het beton bezwijktI e de vloeigrens van het staal wordt bereikt. Bij dit maximale wapeningspercentage is dusgee rotatiecapaciteit meer aanwezig. Dit wapeningspercentage is rechtstreeks in verbando te brengen met een maximale hoogte van de betondrukzone in het bezwijkstadium. Tenaanzien van deze hoogte zullen inde voorschriften bepalingen worden opgenomen opdateen minimaal vereiste rotatiecapaciteit is verzekerd.12Geschematiseerd13GeschematiseerdOok bij deze theorie moet worden voldaan aan de eisen die het statisch evenwicht stelt,terwijl de samenhang van de constructie moet worden verzorgd door de vloeischarnieren.De plaats en het aantal scharnieren moet zodanig worden gekozen dat uit het oogpunt vangeometrie rotatie van deschamieren mogelijk is.Bij het bezwijken zakt de constructie dus in elkaar bij gelijkblijvende belasting en krachts-verdeling. Is het bezwijkmechanisme bekend dan kan volgens de wet van behoud vanenergie de door de belasting verrichte uitwendige arbeid (= belasting X zakking) gelijkworden gesteld aan de inwendige verrichte arbeid (= vloeimoment X hoekverdraaiing).Wanneer het vloeimoment bekend is kan de bezwijkbelasting worden berekend, is daaren-tegen de vereiste bezwijkbelasting gegeven, dan kan het vloeimoment worden bepaaldresp. de doorsnede worden gedimensioneerd. Het bepalen van het vloeimoment, c.q. hetdimensioneren van de doorsnede geschiedt voorts volgens de onderstellingen en met deo-s-dlaqramrnen van het staal en het beton zoals deze in Sb zijn vermeld.oIIIIIIIIIEr zijn uiteraard vele bezwijkmechanismen mogelijk. Het juiste bezwijkmechanisme wordtgevonden door te zoeken naar de ongunstigst denkbare ligging van de vloeischarnieren.Volgens een stelling van Prager zal nl. bezwijken optreden volgensd?t mechanisme datdoor de laagste belasting in beweging kan worden gebracht.De bezwijkbelasting past nu bij de gunstigst denkbare krachtsverdeling die bij dit bezwijk-mechanisme kan optreden. Een andere stelling van Prager zegt nl. dat geen bezwijken zaloptreden zolang nog een krachtsverdeling mogelijk is waarbij evenwicht wordt gemaakt meteen r:og hogere belasting.De stellingen gelden uiteraard indien geen instabiliteitsverschijnselen optreden of breukoptreedt ten gevolge van dwarskracht, wringing e.d.Voor platen is in handboeken voor vele vormen en voorwaarden het juiste bezwijkmechanis-me gegeven. Het komt daarbij voor dat verfijningen zijn aangebracht die enerzijds hetresultaat nauwelijks verbeteren maar anderzijds het rekenwerk bemoeilijken. In de nieuwevoorschriften worden zeer waarschijnlijk aanwijzingen gegeven op grond waarvan met eenzo eenvoudig mogelijk vloeilijnenpatroon mag worden gerekend.De elementaire bezwijkanalyse en de vloeilijnentheorie geven ten aanzien van het wapeneneen grote vrijheid en bieden de mogelijkheid een wapening aan te brengen die niet over-eenkomt met die welke voortvloeit uit de lineaire elasticiteitstheorie, Dit kan tot economischeconstructies leiden. Wanneer al te ver van de lineair elastische krachtsverdeling wordt af-geweken dan is het mogelijk dat in een vroeg stadium vloeischarnieren optreden, Dit zouonaanvaardbare scheurvorming of doorbuiging in het gebruiksstadium tot gevolg kunnenhebben. Vooral ten aanzien van wisselende belastingen is het optreden van vloeischarnierenin dit stadium niet gewenst. Inzake de scheurvorming en de doorbuiging zullen nadere richt-lijnen worden gegeven.Cement XXII (1970) nr. 8 3515d De evenwichtsmethodeVolgens de evenwichtsmethode kan men zelf een systeem van belastingafdracht naar deondersteuningen kiezen. Hierbij dient te worden voldaan aan de eisen die het statischevenwicht stelt. De samenhang in de constructie wordt buiten beschouwing gelaten. Is een-maal een systeem gekozen, dan moeten uiteraard wel alle consequenties van het systeemin de dimensionering van de constructie worden verdisconteerd.Hoewel deze methode de minst elegante is van de besproken methoden, leidt deze volgensde laatst genoemde stelling van Prager onder 5c tot veilige uitkomsten. Uiteraard is ditalleen het geval als het materiaal voldoende plastische vervormingen toestaat, opdat degekozen belastingafdracht inderdaad in het bezwijkstadium kan optreden. Ook in dit gevalmag geen voortijdig bezwijken ontstaan door instabiliteit, dwarskracht, wringing e.d.De methode leidt dus tot een grote mate van vrijheid ten aanzien van de ligging van dewapening. Het is echter wenselijk een systeem te kiezen dat in grote lijnen de aard van deconstructie niet aantast en dat kan worden ontleend aan inzichten die met ??n der eerderbesproken methoden zijn verkregen. Dit is ook om economische redenen wel geboden.Hoe onhandiger het gekozen systeem constructief gezien is, des te meer wapening hetvereist.De dimensionering wordt ook bij deze methode betrokken op het bezwijkstadium en volgensde onderstellingen en c-e-dlaqrammen zoals vermeld onder 5b. Ook bij deze methode zalde constructie moeten voldoen aan eisen inzake scheurvorming en doorbuiging.6 De besproken berekeningsmethoden zullen dus alle in de nieuwe betonvoorschriften alsmogelijkheden worden geboden voor de berekening van de krachtsverdeling in betoncon-structies. Voor de verschillende constructietypen zijn niet alle methoden bruikbaar. In detabel zijn de mogelijkheden samengevat. In alle gevallen vindt de dimensionering van de-, doorsnede plaats volgens de niet-lineaire elasticiteitstheorie.dlmenslonertnq van dekrachtsverdeling doorsnedebuiging (+ normaalkracht)liggers, platenpaddestoelvloerenkolommen, wandenlineaire ef.-thecrte (metplastische overwegingen)element. bezwijkanalysec.q. vloeilijnentheorieevenwichtsmethode(niet-lineaire eL-theorie)lineaire eL-theorie (metplastische overwegingen)niet-lineaire eL-theorielineaire eL-theorie +aanvullende eisenniet-lineaire eL-theoriemet standaard diagramvoor betonniet-lineaire eL-theorieniet-lineaire eL-theoriemet standaard diagramvoor betonniet-lineaire eL-theorie niet-lineaire el-theorieraamwerkenlineaire eL-theorie +aanvullende eisenniet-lineaire eL-theoriemet standaard diagramvoor betonCement XXII (1970) nr. 8In die gevallen, waarin kruipverschijnselen een belangrijke rol kunnen spelen ten aanzienvan de krachtsverdeling, is de toepassing van de methoden beperkt tot de niet-lineaireelasticiteitstheorie en tot de lineaire elasticiteitstheorie met aanvullende eisen. Met betrek-king tot de dimensionering van de doorsnede kunnen, door het invoeren van het standaard-diagram voor beton,langeduureffecten geacht worden te zijn verdisconteerd. Ten aanzienvan wisselende belasting, waarvan over de invloed op de krachtsverdeling en de sterktenog weinig bekend is, blijft in die gevallen waarin relatief grote wisselende momenten en/ofnormaalkrachten optreden voorzichtigheid geboden. In dit verband kan worden vermeld datin het kader van de CUR in de komende jaren onderzoekingen zullen plaatsvinden naar hetgedrag van kolommen onder wisselende belasting.Resumerend mag worden gesteld dat, ondanks enkele lacunes in de kennis omtrent hetgedrag van gewapend-betonconstructies, de opzet van de nieuwe voorschriften- een goedestap vooruit l?kt naar het w?rkel?k construeren!352

Reacties