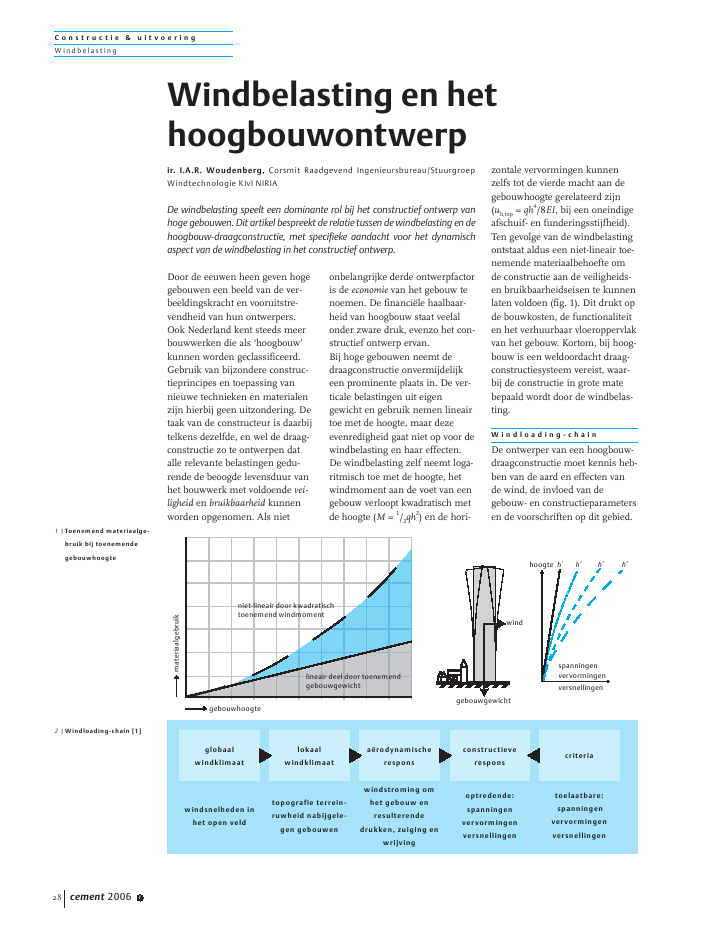
C o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 128Door de eeuwen heen geven hogegebouwen een beeld van de ver-beeldingskracht en vooruitstre-vendheid van hun ontwerpers.Ook Nederland kent steeds meerbouwwerken die als `hoogbouw'kunnen worden geclassificeerd.Gebruik van bijzondere construc-tieprincipes en toepassing vannieuwe technieken en materialenzijn hierbij geen uitzondering. Detaak van de constructeur is daarbijtelkens dezelfde, en wel de draag-constructie zo te ontwerpen datalle relevante belastingen gedu-rende de beoogde levensduur vanhet bouwwerk met voldoende vei-ligheid en bruikbaarheid kunnenworden opgenomen. Als nietonbelangrijke derde ontwerpfactoris de economie van het gebouw tenoemen. De financi?le haalbaar-heid van hoogbouw staat veelalonder zware druk, evenzo het con-structief ontwerp ervan.Bij hoge gebouwen neemt dedraagconstructie onvermijdelijkeen prominente plaats in. De ver-ticale belastingen uit eigengewicht en gebruik nemen lineairtoe met de hoogte, maar dezeevenredigheid gaat niet op voor dewindbelasting en haar effecten.De windbelasting zelf neemt loga-ritmisch toe met de hoogte, hetwindmoment aan de voet van eengebouw verloopt kwadratisch metde hoogte (M = 1/2qh2) en de hori-zontale vervormingen kunnenzelfs tot de vierde macht aan degebouwhoogte gerelateerd zijn(uh,top= qh4/8EI, bij een oneindigeafschuif- en funderingsstijfheid).Ten gevolge van de windbelastingontstaat aldus een niet-lineair toe-nemende materiaalbehoefte omde constructie aan de veiligheids-en bruikbaarheidseisen te kunnenlaten voldoen (fig. 1). Dit drukt opde bouwkosten, de functionaliteiten het verhuurbaar vloeroppervlakvan het gebouw. Kortom, bij hoog-bouw is een weldoordacht draag-constructiesysteem vereist, waar-bij de constructie in grote matebepaald wordt door de windbelas-ting.W i n d l o a d i n g - c h a i nDe ontwerper van een hoogbouw-draagconstructie moet kennis heb-ben van de aard en effecten vande wind, de invloed van degebouw- en constructieparametersen de voorschriften op dit gebied.Windbelasting en hethoogbouwontwerpir. I.A.R. Woudenberg, Corsmit Raadgevend Ingenieursbureau/StuurgroepWindtechnologie KIvI NIRIADe windbelasting speelt een dominante rol bij het constructief ontwerp vanhoge gebouwen. Dit artikel bespreekt de relatie tussen de windbelasting en dehoogbouw-draagconstructie, met specifieke aandacht voor het dynamischaspect van de windbelasting in het constructief ontwerp.materiaalgebruikgebouwhoogteniet-lineair door kwadratischtoenemend windmomentlineair deel door toenemendgebouwgewichtgebouwgewichtwindhoogtespanningenvervormingenversnellingenh1h2h3h4globaalwindklimaatlokaalwindklimaata?rodynamischeresponsconstructieveresponscriteriawindsnelheden inhet open veldtopografie terrein-ruwheid nabijgele-gen gebouwenwindstroming omhet gebouw enresulterendedrukken, zuiging enwrijvingoptredende:spanningenvervormingenversnellingentoelaatbare:spanningenvervormingenversnellingen1 |Toenemend materiaalge-bruik bij toenemendegebouwhoogte2 |Windloading-chain [1]C o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 1 29De windloading-chain (fig. 2)maakt overzichtelijk welke para-meters een rol spelen bij het ont-werpen van een bouwwerk opwindbelasting. De eerste tweeparameters uit de windloading-chain zijn het globale en lokalewindklimaat. Deze vormen teza-men de windomgeving van hetgebouw en zijn afhankelijk van degebouwlocatie. De mate waarin dewind wordt omgezet naar eenbelasting op het gebouw, wordt dea?rodynamische respons genoemd.Bepalend hierbij zijn met namede gebouwvorm en ?afmetingen.Omdat de wind een dynamischebelasting is, wordt de in rekeningte brengen belasting medebepaald door de dynamischeeigenschappen van de constructiezelf. Hoe de constructie op dezedynamische belasting reageert,wordt de constructieve responsgenoemd, die is uit te drukken intermen van spanningen, vervor-mingen en versnellingen. Dezezijn te berekenen volgens de leervan de mechanica en moeten vol-doen aan de criteria als vastgelegdin de voorschriften.NEN 6702 [2] schrijft de windbe-lasting voor, door waarden tegeven voor de verschillende facto-ren uit de windloading-chain. Hetglobale en lokale windklimaat ver-taalt zich in de te hanteren stuw-druk en de a?rodynamische res-pons in een windvormfactor Cteneen Cdim. Als alternatief kan wind-tunnelonderzoek worden verrichtom de a?rodynamische respons tebepalen.Uit oogpunt van veiligheid enbruikbaarheid worden grenzengesteld aan de constructieve res-pons. In NEN 6700 is onder meerhet veiligheidsniveau vastgelegdwaaraan constructies moeten vol-doen. In de praktijk werkt menmeer met de materiaalgebondennormen van de 6700-serie en deeerder genoemde belastingnormNEN 6702. De materiaalnormen,zoals NEN 5950, geven op hunbeurt rekenprocedures en criteriaom het materiaal van de draagcon-structie te toetsen, zoals demateriaalspanningen maar ook destabiliteit van de constructie-elementen.Daarbij zal in de toekomst gewerktgaan worden met de Eurocode,waarin de internationale kennis isgebundeld. In deze code zijn ookop het gebied van de windbelastingcriteria geformuleerd voor de con-structieve respons.W i n d a l s d y n a m i s c h eb e l a s t i n gStatische belastingen worden relatieflangzaam op een constructie aan-gebracht en zijn onveranderlijk vankarakter. Voorbeelden hiervan zijnbelasting door eigen gewicht,gebruikers, sneeuw, regenwater,temperatuur en zettingen. Dynami-sche belastingen worden plotselingaangebracht en veranderen snelvan grootte en richting. Het is vaakmoeilijker om vast te stellen wat deexacte aard van de dynamischebelastingen is en hoe de construc-tie zich onder deze belastingengedraagt. Onder dynamische belas-tingen vallen onder meer de belas-tingen door aardbeving en wind.Daarbij ligt de trillingsfrequentievan aardbevingen gemiddeld tus-sen de 1 en 10 Hz, en die van dewind tussen de 0,01 en 1 Hz (fig.3). Dientengevolge is hoogbouw,met een eigenfrequentie onder de1 Hz over het algemeen gevoeligervoor windbelasting dan voor aard-bevingen.Windbelasting is als zodanig eendynamische belasting. De windbe-lasting is gerelateerd aan de wind-snelheid u (p = u2). Het aardop-pervlak zorgt voor een turbulentewind. De tijdsafhankelijkewindsnelheid U(t) kan wordenopgedeeld in een tijdsgemiddeldestatische component u(z) en tijds-afhankelijke dynamische compo-nent u~(t). De statische componentu(z) neemt logaritmisch toe metde hoogte door de afnemendeinvloed van de wrijving. Dit isweergegeven in figuur 4, waarbijook voor een bepaald punt eenindruk wordt gegeven van de vari-atie om de tijdsgemiddelde com-ponent.Volgens NEN 6702 is een dynami-sche belasting een belasting dieversnellingen van meer dan0,5 m/s2kan veroorzaken in debouwconstructie of onderdelendaarvan. Versnellingen die zich bijgebouwen onder invloed van windvoordoen, liggen bij hoogbouwechter in de grootte-orde van 0,1 ?hoogbouw laagbouwaardbevingwindfrequentie (Hz)0,001 0,01 0,1 1 10belasting3 |Belastingsspectrum voorwind en aardbeving [4]zu~(t)u~(z)u~(t)u?(z)U(t)U(z,t)tU(t)U(t)4 |Fluctuatie van windsnel-heid om een tijdsgemid-delde en met de hoogteC o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 1300,2 m/s2. NEN 6702 kent daaromook nog het begrip quasi-statischebelasting. Dit zijn dynamischebelastingen waarvan het dyna-misch deel relatief gezien beperktis. Windbelasting is volgens hetvoorschrift dan ook een quasi-sta-tische belasting. Volgens NEN6702 mag de constructie statischworden doorgerekend, waarbij hetdynamische effect wordt meege-nomen door de dynamische ver-grotingsfactor, 1. Deze factor isafhankelijk van de opbouw van dewindbelasting, de gebouwafmetin-gen en de constructieve eigen-schappen zoals stijfheid, massa endemping.C o n s t r u c t i e v e r e s p o n sDe reactie van de constructie opde (wind-)belasting wordt de con-structieve respons genoemd. Degeometrie van het gekozen draag-systeem bepaalt de interne krach-ten uit de windbelasting, die inmateriaalspanningen te vertalenzijn. Onder invloed van dezespanningen treden lokale en glo-bale vervormingen op. Doordat devervormingen onder de dynami-sche windbelasting tijdsafhanke-lijk zijn, ontstaan versnellingen.Aangaande de constructieve res-pons moeten de verschillendedimensies in ogenschouw wordengenomen: hoogterichting, lengte-richting, dwarsrichting, draairich-ting en de tijdsdimensie. Zo kanop materiaalniveau wordengedacht aan normaalspanningen,schuifspanningen en wringspan-ningen, al dan niet tijdsafhanke-lijk.Ook verplaatsingen en versnellin-gen treden op in de verschillenderichtingen: parallel aan en dwarsop de windrichting en in de draai-richting. Veelal wordt voor gebou-wen alleen gekeken naar effectenin de richting van de wind. Trillin-gen dwars op de wind kunnenechter ook optreden, bijvoorbeelddoor turbulentie dwars op dewindrichting, maar eerder nogvortex-shedding. Daarnaast zaltorsie optreden bij een excentrici-teit tussen het zwaartepunt van deresulterende windbelasting en hetdwarskrachtencentrum van deconstructie. De optredende torsiekan worden versterkt door eenexcentriciteit tussen het massa-zwaartepunt en het dwarskrach-tencentrum van de constructie.S t a b i l i t e i t s s y s t e m e nOver het algemeen wordt de wind-belasting op een gebouw door degevel naar de vloeren afgedragen.De vloeren dragen de belastingvervolgens via schijfwerking afnaar de constructie die de hori-zontale windbelasting op een sta-biele wijze verticaal afdraagt naarde fundering. In de loop der jarenzijn verschillende constructieprin-cipes ontwikkeld die de stabiliteitkunnen verzorgen. Algemeenbekend zijn de raamwerkconstruc-tie, stijve-kernconstructie, gevel-buisconstructie, megaconstructieen diverse combinaties. De keuzevoor een van deze systemen issterk afhankelijk van de hoogte enslankheid, architectuur en platte-grond van een gebouw. Elk geko-zen stabiliteitssysteem is uiteinde-lijk een specifiek antwoord op eenunieke reeks van ontwerpvragen.M o d e l l e r e n v a n d ec o n s t r u c t i eOm het gedrag van een gekozengebouwconstructie te analyserenmoet een rekenmodel wordenopgezet. Daarbij zullen allereerstde hoofdafmetingen van hetgebouw en de constructie moetenworden vastgelegd. Hieruit volgenook de aan te houden belastingen.Aanvullend moeten de doorsnede-afmetingen van de constructieveelementen worden vastgelegd,samen met de gewenste materiaal-eigenschappen. Vervolgens kan deconstructie worden gemodelleerden doorgerekend, ter verkrijgingvan de constructieve respons.Daarop volgt de controle van desterkte, stijfheid, stabiliteit ensamenhang van de constructie, opniveau van de constructie als totaal,dan wel op doorsnedeniveau.EI.GACf5 |Eendimensionaalmechanicamodel van eenstabiliteitsconstructietopEIEI GACftopGACfEI GA Cf+ +=EIqh48EIGA;qh22GACf;qh32Cf= = =top qwindh48EIh22GAh32Cf+ + =6 |Werking van een 1D-mechanicamodel metbuiging, afschuiving enfunderingsrotatieC o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 1 31Omdat in het ontwerptraject vangrof naar fijn wordt gewerkt, heb-ben bovengenoemde stappen tel-kens op meer gedetailleerd niveauplaats. Daarnaast is het voor hoog-bouw niet ongebruikelijk in eendefinitiever ontwerpstadium eendriedimensionaal computermodelvan de constructie te maken. Eendergelijk computermodel zou ineen vroeg ontwerpstadium hetdoel voorbij schieten en boven-dien een ongewenste schijnnauw-keurigheid voorspiegelen.1 D - m e c h a n i c a m o d e lDe meest eenvoudige representa-tie van een stabiliteitsconstructieis het ??ndimensionale mechani-camodel (fig. 5), waarin de con-structie wordt beschreven meteen rotatieveer ten behoeve vande funderingsstijfheid (Cf), staafmet buigstijfheid (EI) en afschuif-stijfheid (GA) en een staaflengtegelijk aan de gebouwhoogte (h).Wanneer wordt gekeken naar destijfheid van een constructie en deoptredende vervormingen bij eenhorizontale (wind-)belasting, kande totale vervorming in drie com-ponenten worden onderverdeeld:buiging, afschuiving en funde-ringsrotatie. In figuur 6 zijn daar-om de vervormingsdiagrammengetekend voor de afzonderlijkestijfheidsmechanismen, uitgaandevan een gelijkmatig verdeeldehorizontale lijnlast q.Met deze basis-schematiseringvan de constructie kan in eenvroeg ontwerpstadium eeninschatting worden gemaakt vande benodigde constructie-afme-tingen. Hiervoor zijn aannamesnoodzakelijk van onder meer deE-modulus, doorsnede- en stijf-heidsreducties door (raam-)spa-ringen, scheurvorming, invloedvan verbindingen, funderings-stijfheid enz. Om het model han-teerbaar en helder te houden zijnsimplificaties gewenst, maarmoet de essentie worden behou-den. Het ??ndimensionalemechanicamodel kan op velerleiwijze worden uitgebreid naargelang de complexiteit van hetontwerp en het stadium waarinhet zich bevindt.T w e e d e - o r d e - e f f e c tBij de berekening van de stabili-teitsconstructie van een hooggebouw is het zogenoemde tweede-orde-effect veelal niet te verwaarlo-zen. De windbelasting zorgt vooreen eerste-ordeverplaatsing. Dezeverplaatsing veroorzaakt een ex-centriciteit van de verticale belas-tingen, waardoor een versterkingvan de verplaatsingen optreedt.Dit verschijnsel wordt het tweede-orde-effect genoemd (fig. 7). Demate waarin dit effect optreedt,hangt af van de stijfheidseigen-schappen van de stabiliteitscon-structie en de grootte van de verti-cale belastingen op de constructiezelf en op de aanpendelendedelen. Deze parameters bepalende knikfactor n, die vervolgens denQkQoptr1qm1h h38EI 2GAh22Cf+ + = =qwindhq1mhq2mhqm= q1m+ q2mq1mq2mh/2h/2qwindCfdtop,0dtop,0/2EI,GAverticale belasting op destabiliteitsconstructie (q1m)aanpendelendebelasting (q2m)top eind,nn 1?top 0, ;= nQkQoptruit het kritieke evenwicht volgt (bij benadering van de buigvorm):knikkracht waarbij: Q k= qmh = Q optr=voor de totale topverplaatsing:=qwind h 1/21/2hqmh top 0, qmhqwindh2top 0,= =top,0 qwindh48EIh22GAh32Cf+ + =Qkqwindh2top 0,1h28EI12GAh2Cf+ + = =n ofwel:QkQoptr1qm1h h38EI 2GAh22Cf+ + = =1nqmh h38EI 2GAh22Cf+ + =qwindh2top 0,7 |Werking van het tweede-orde-effectC o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 132vergrotingsfactor n/n-1 bepaalt.Deze vergrotingsfactor kan wor-den afgeleid volgens de exercitiein het kader op blz. 31 en ligt overhet algemeen tussen de 1,0 en 1,2.D y n a m i s c h e c o n s t r u c -t i e v e e i g e n s c h a p p e nHet dynamisch gedrag van eendoor wind belaste constructiewordt met name bepaald door destijfheid, massa en demping. Deontwikkeling van moderne materi-alen en constructietechniekenleidt tot steeds slankere hoog-bouw, met minder constructiema-teriaal, minder massa en minderdemping. Hierdoor neemt hetdynamisch effect van de windbe-lasting toe.Het dynamisch gedrag van de sta-biliteitsconstructie kan theoretischworden geanalyseerd en gesche-matiseerd met een massa-veer-dem-persysteem (fig. 8). Het dynamischgedrag wordt daarin bepaald doorde dynamische belasting (f(t)),effectieve stijfheid (ke), effectievemassa (me) en effectieve demping( of D).De dynamische vergrotingsfactor1uit NEN 6702 is naar ditsysteem terug te herleiden. DeNEN geeft grafieken en formulester bepaling van 1. Hiervoor moe-ten de gebouwafmetingen (b enh), de eigenfrequentie (fe) en dedemping (D) bekend zijn. Deeigenfrequentie is een maat voorde dynamische stijfheid van hetgebouw, waarin gebouwmassa enstijfheid zijn verwerkt. De dem-ping is een maat voor de opnamevan trillingsenergie, die bepaalthoe snel een trilling wordt uitge-dempt. Deze demping heeft inconstructieve en niet-constructievematerialen plaats, en in eventueelkunstmatig toegevoegde demping.De waarde van de vergrotingsfac-tor 1varieert meestal tussen de1,0 en 1,2. Bij een factor 1,0 kanhet dynamisch effect worden ver-waarloosd. Bij waarden groter dan1,2 moet het dynamische effect opnauwkeuriger wijze worden mee-genomen.EigenfrequentieDe stijfheid en massa komensamen in de eigenfrequentie. Omte beginnen kan worden gekekennaar de eerste eigenfrequentie, dievaak bepalend is voor de belang-rijkste dynamische respons. Vol-gens de mechanicatheorie geldtvoor de eerste eigenfrequentie vaneen systeem met een bepaaldestijfheid k en massa m:1 k 1 kf1= ____ __ (1 ? D2) ____ __2 m 2 mDe demping (D) heeft bij eenwaarde van 0,010 ~ 0,020 een teverwaarlozen invloed op de eigen-frequentie. Op deze theoretischeformule is NEN 6702 gebaseerd.Daarbij is in de NEN tevens uitge-gaan van een buigligger (GA isoneindig). Een gebouwconstructiezal in het algemeen niet geheel alseen buigligger vervormen, maarook deels als een afschuifligger.Dit wordt in de NEN niet meege-nomen, wat een conservatievebenadering is, omdat bij eenafschuifligger de effectieve massagroter is.Uit een groot aantal gemeteneigenfrequenties van hoge gebou-wen kan de eigenfrequentie wor-den benaderd met fe= 46/gebouw-hoogte, hoewel zeer grof en geldigtot een hoogte van ongeveer200 m.De eerste eigenfrequentie voortorsie ligt in het algemeen wathoger, in de ordegrootte fe= 72/gebouwhoogte. Problemen kun-nen zich voordoen wanneer beideeigenfrequenties dicht bij elkaarliggen, waardoor zich een gekop-pelde respons kan voordoen. Indit geval is het verstandig de opzetvan de constructie zo te verande-kef(t)me of DdmaxdmindmaxtTe = 2//2??n volledige trillingx t( ) max t( )sin=v t( ) max t( )cos=a t( ) ?2max t( )sin= 2fe2Te= =fe12 12km= =amax 2max 2fe( ) max (amax ga )= = =aamaxg=g 3 5,Uit de harmonische trilling kunnen de volgendeparameters worden afgeleid:maximale versnelling:standaardafwijking van de:waarbij de piekfactor: volgens NEN67028 |Massa-veer-dempersys-teem9 |Karakteristieken van eenharmonische trillingC o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 1 33ren dat deze op een andere wijzeweerstand biedt tegen translatieen rotatie in het horizontale vlak.H i n d e r l i j k h e i d g e b o u w -b e w e g i n g e n d o o r w i n dOnder invloed van de windbelas-ting kunnen zich onacceptabelegebouwbewegingen voordoen,ondanks dat constructieve veilig-heid is verzekerd. Hoe mensen opeen gebouwbeweging reageren,hangt af van diverse factoren,zoals richting van de beweging,activiteit van de waarnemer (rus-ten, lopen, werken, wonen), hoesterk, hoe vaak en wanneer hetzich voordoet, of het hoorbaar danwel zichtbaar is, enz.De dynamische vervormingen vaneen gebouw kunnen wordenbestudeerd aan de hand van eenharmonische trilling (fig. 9). Nietde uitwijking zelf, maar de ver-snelling van de beweging bepaalthet discomfort. Zo voelt een per-soon in een rijdende auto niets bijconstante snelheid, maar wel watbij versnelling of vertraging.Met de formules voor een harmo-nische trilling kan de maximaleversnelling (amax) door een piekfac-tor (g) worden uitgedrukt in destandaardafwijking van de versnel-ling (a) en vice versa. Daarbijhangt amaxalleen nog af van deeigenfrequentie van de constructie(fe) en de maximale topverplaat-sing (max) onder invloed van dedynamische belasting.C o m f o r t c r i t e r i a u i tN E N 6 7 0 2Mensen ervaren in het algemeeneen versnelling van 1,5% van degravitatieversnelling (g) als hinder-lijk; dit is 0,15 m/s2. Deze waardezou als maximum kunnen wordengehanteerd voor de optredendeversnelling in een hoog gebouw,met daarbij de toelaatbare herha-lingstijd van optreden. NEN 6702geeft een criterium dat een limietstelt aan de horizontale versnellin-gen die hoogstens eenmaal perjaar mag worden overschreden.Deze limiet is iets genuanceerderdan de 0,15 m/s2en is afhankelijkgesteld van de eigenfrequentie vanhet gebouw, alsmede de gebruiks-functie (zie hiervoor figuur 21 vanNEN 6702). Voor eigenfrequentiesonder de 1,0 Hz neemt de toelaat-bare versnelling toe naarmate defrequentie afneemt. Voor kantorenis de limiet gesteld op 0,5 m/s2voor een eigenfrequentie van0,1 Hz, lineair afnemend tot0,2 m/s2voor 1,0 Hz en daarbo-ven. Voor een woonfunctie is delimiet gesteld op 0,2 m/s2vooreen eigenfrequentie van 0,1 Hz,lineair afnemend tot 0,1 m/s2voor1,0 Hzen daarboven. De eerder genoem-de hinderlijkheidsgrens van0,15 m/s2is als zodanig een aar-dig gemiddelde voor de hogerefrequenties.Dat de eisen voor een woon- ofslaapgebouw strenger zijn, heeftonder meer als oorzaak dat degewaarwordingsdrempel lager ligtbij stilstaande personen dan bijlopende of anderszins actieve per-sonen. Ook bij direct contact tus-sen het hoofd en het in bewegingzijnde gebouw, bijvoorbeeld bijslapen, wordt men zich eerder vande beweging gewaar. Daarnaastzijn mensen een groter deel vande dag in huis aanwezig dan opkantoor.Onderzoek heeft daarnaast aange-toond dat bij zeer geconcentreerdwerk de gewaarwordingdrempelwel eens lager kan liggen dan voorwoningen. Daarentegen zou bijfysieke arbeid de drempel hogerliggen dan voor kantoren. Ditonderscheid is in NEN 6702 (nog)niet gemaakt.P o s i t i e f b e ? n v l o e d e n v a nh e t d y n a m i s c h g e d r a gConform het massa-veer-demper-systeem kunnen maatregelentegen een overmatig dynamischgedrag worden gevonden in hetbe?nvloeden van de dynamischebelasting (f(t)), effectieve stijfheid(ke), effectieve massa (me) eneffectieve demping ( of D). Depraktische mogelijkheden enonmogelijkheden worden kortbesproken.Dynamische windbelastingbe?nvloedenDe dynamische windbelasting(f(t)) is een gegeven zodra locatie,vorm en afmetingen van hetgebouw vastliggen. De construc-tief ontwerper zal of kan dezeparameters vaak weinig be?nvloe-den. Wanneer we echter kijkennaar het zogenoemde vortex-shed-ding, dan kan de vorm behoorlijkinvloed hebben op het karaktervan de uiteindelijke dynamischebelasting.Doordat (hoge) gebouwen veelalongestroomlijnd zijn, zal de stro-ming scheiden in plaats van degebouwcontouren te volgen. Bijhet loslaten van de windstroomontstaan wervels. De wervels latenbeurtelings los, wat vortex-shed-ding wordt genoemd. Het gebouwondervindt zo een fluctuerendebelasting loodrecht op de wind-richting. De wervelvorming wordtbe?nvloed door de vorm van hetgebouw en de structuur van dewind. De aanwezigheid van ande-re, gelijkvormige gebouwen aande wind-opwaartse zijde kan wer-velvorming sterk be?nvloeden.Vortex-shedding treedt altijd op.Het wordt pas een probleem alsde wervels grote drukverschillenteweegbrengen en/of gelijktijdigover een groot deel van degebouwhoogte optreden. Om dittegen te gaan, kan de gebouw-vorm met de hoogte worden aan-10 | Voorbeelden vangebouwvormen die destructuur van wervel-vorming verstoren(v.l.n.r.: Burj Dubai,Guangzhou TV andSightseeing Tower,Taipei 101) [6]C o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 134gepast of kunnen verstoringenworden aangebracht in de vorm.Voorbeelden zijn gegeven infiguur 10. Slechts bij zeer slankegebouwen kan wervelvorming eenrol spelen in het ontwerp. Bijschoorstenen daarentegen is hetheel gebruikelijk om met vortex-shedding rekening te houden.Veelal worden daarvoor stripsrond de schoorsteen aangebracht,om de structuur van de wervelvor-ming te breken.Effectieve stijfheid be?nvloedenDe effectieve stijfheid (ke) is voorgebouwen sterk van invloed op degebouwversnelling. Wel neemt deinvloed af met toenemendegebouwhoogte. Figuur 11 geefttwee gebouwen weer die net aanhet comfortcriterium uit ISO 6897voldoen. Gebouw A is slank meteen eigenfrequentie van ongeveer0,2 Hz en gebouw B is gedrongenmet een eigenfrequentie van0,9 Hz. Per gebouw zijn de effec-ten berekend van de massa, stijf-heid en demping op de standaard-afwijking van de versnelling a.De pijlen in figuur 13 wijzen in derichting van een toename van destijfheid, massa of demping. Uithet figuur blijkt dat het vergrotenvan de stijfheid slechts geringeinvloed heeft op de standaardaf-wijking van de versnelling, a.Wanneer het dynamisch gedraggeringe be?nvloeding behoeft, kande stijfheid worden aangepast. Bijzeer slanke gebouwen (h/b > 6 ),waar het dynamisch effect van dewindbelasting het grootst is, zullenstijfheidsvergrotende maatregelenweinig effectief zijn. Hier zalgezocht moeten worden naar ver-groting van de massa of demping.Effectieve massa be?nvloedenDe effectieve massa (me) wordtbepaald door de gebouwmassa, demassaverdeling over de hoogte ende uitbuigingsvorm van de con-structie. Een vergroting van detotale gebouwmassa verkleint degebouwversnelling bij eenzelfdedynamische belasting (f = ma). Ditzou echter meer materiaal enhogere belastingen op de funde-ring betekenen, wat een kostbaremaatregel is.De effectieve massa kan ook wor-den vergroot door de uitbuigings-vorm van het gebouw aan te pas-sen, zodanig dat bij eenzelfdewindbelasting meer massa inbeweging wordt gebracht, waar-door de optredende versnellingafneemt. Een constructie diewerkt als buigligger heeft eentweemaal kleinere effectievemassa dan een gebouw metdezelfde massa(-verdeling), maarmet de vervormingseigenschap-pen van een afschuifligger. Ditkan worden herleid.Voor een vrij trillend systeemgeldt dat de maximale kinetischeenergie, optredend bij de nuldoor-gang, gelijk is aan de maximalepotenti?le energie, bij maximaleuitwijking. Dit correspondeertmet figuur 9 van de harmonischetrilling. Wanneer nu niet alleennaar de topuitwijking wordt geke-ken, dan bepaalt de horizontaleverplaatsing op elk punt de poten-ti?le energie van dat punt. In depositie van maximale uitwijkingkan de totale potenti?le energieover de hoogte worden ge?nte-greerd. Wanneer de massa's voorde buigligger en afschuifliggergelijk zijn, kan de effectieve massaeenvoudig worden vastgestelddoor de oppervlakken tussen derechte staafas en de gebogen ofafgeschoven staafas te vergelijken(fig. 12). Bij een afschuifligger isdit oppervlak een factor 2 groterdan bij een buigligger.Om de uitbuigingsvorm en daar-mee de effectieve massa positief tebe?nvloeden, kan in plaats van eenkernconstructie een raamwerkcon-structie worden toegepast, of eencombinatie van een kern met over-drachts- of raamwerkconstructie.Tevens kan een herverdeling vande massa leiden tot een grotereeffectieve massa.11 | Effectiviteit van stijf-heid (k), massa (m) endemping () op degebouwbeweging [5]0,100,010,10 1,00iso-criteriummkmkgebouw A:'slank'gebouw B:'plomp'a(m/s2)fe(Hz)fe12gmiimii2=dtopdEIdGAmtopAEIEIbuiging afschuivingGAAGA= 2AEImidi12 | Eigenfrequentie eneffectieve massa inrelatie tot buigvormC o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 1 35Demping be?nvloedenDemping ( of D) is ongetwijfeldde meest effectieve manier om hetdynamisch gedrag van een con-structie positief te be?nvloeden enhinderlijke gebouwtrillingen tebeperken. De demping kan uitconstructieve en niet-constructievematerialen komen, waarbij deinvloed van de laatste veelal wordtverwaarloosd. Daarnaast kankunstmatig demping worden toe-gevoegd. De demping door langs-stromende lucht, zogenoemdea?rodynamische demping, wordtmeestal verwaarloosd. Echter, bijconstructies met geringe massaen lage eigenfrequenties kan dezeeen belangrijke bijdrage leveren.De materiaaldemping is afhanke-lijk van het gebruikte materiaal ende uitwijking gerelateerd aan degebouwhoogte (tabel 1). NEN6702 maakt alleen onderscheidnaar materiaal. Zo is de dem-pingsmaat voor een staalconstruc-tie sterk afhankelijk van de soortverbindingen. Een lasverbindingis stijf, terwijl bij het slippen vanboutverbindingen energie wordtomgezet in warmte, hetgeen dem-ping veroorzaakt.Het materiaal beton heeft dooreen groter `hysteresis'-gedrag eenhogere demping dan staal. Bijbeton hangt de dempingsmaat afvan de mate van aanwezigheidvan scheuren. Als de breukvlak-ken in een scheur langs elkaarbewegen, wordt namelijk doorwrijving energie geabsorbeerd. Dedempingsmaat van ongescheurdbeton heeft zo een waarde van0,007 tot 0,010, terwijl de dem-pingsmaat voor gescheurd beton0,010 tot 0,040 bedraagt. Dit bete-kent voor hogesterktebeton ofbeton met voorspanning wellichteen lagere dempingsmaat danvoor een gemiddelde betonsterkte-klasse.NEN 6702 hanteert voor zowel desterkte- als stijfheidsberekeningende volgende dempingswaarden:D = 0,01 voor staalconstructies enD = 0,02 voor betonconstructies.Echter, voor toetsing van het tril-lingscomfort hanteert NEN 6702een D-waarde van 0,01 voor zowelstaal als beton (bij fe< 1Hz). Voorbeton is dit dus lager dan de eer-der genoemde waarde van 0,02.Dit zou kunnen worden verklaarddoor het feit dat wanneer mennaar comfort kijkt, de optredendespanningen lager zijn en hierdoorminder scheurvorming in hetbeton optreedt. Onder extremebelastingen zal meer scheurvor-ming optreden dan onder fre-quenter voorkomende belastin-gen. Toch kunnen ook in degebruikstoestand al scheuren inhet beton aanwezig zijn, bijvoor-beeld door uitzetten en krimp vanhet beton en door de belastingsge-schiedenis van de constructie.Bij gebouwen die zich zeer dyna-misch gedragen kan de additioneledemping het dynamische gedragverbeteren. Hierin zijn twee prin-cipes te onderscheiden: passieveen actieve demping. Passievedemping is het principe waarbijenergie wordt geabsorbeerd, zon-der dat deze wordt geregeld ofteruggekoppeld met de gebouwbe-weging. Bij het principe van actie-ve demping wordt de gebouwbe-weging gecontroleerd gedemptdoor een regelsysteem met terug-koppeling en een externe energie-bron. Tabel 2 geeft een beknoptoverzicht van verschillende dem-pingprincipes. De meest toegepas-te principes zijn de visco-elasti-sche demper en de zogenoemdeafgestelde massademper, in hetengels Tuned Mass Damper.De visco-elastische demper isgebaseerd op het principe van vis-cositeit, taaie vervormbaarheid,van een materiaal. Dit soort dem-per kan bijvoorbeeld opgebouwdzijn uit staalplaten met daartussenhet visco-elastische materiaal. Dedempers moeten worden aange-bracht alwaar vervormingen optre-den, waar de dempers deze ver-vormingsenergie omzetten inwarmte. Visco-elastische demperswaren toegepast in de als vakwerkuitgevoerde vloerliggers van hetWorld Trade Center in New York.De Tuned Mass Damper is geba-seerd op de massatraagheid vaneen toegevoegde massa. Dezemassa bedraagt meestal 0,5% tot1,0% van de totale gebouwmassa.Aan deze massa is een systeembevestigd dat energie dissipeerttijdens de relatieve beweging vande massa, bijvoorbeeld veren ofpneumatische dempers. De dem-pers kunnen worden afgesteld(`getuned') op de gebouwfrequen-tie. Als het gebouw beweegt zul-len de dempers door de traagheidvan de massa worden ingedruktdan wel uitgetrokken, waardoor degebouwbeweging wordt tegenge-werkt. De optimale massa en fre-quentie van het systeem zijn theo-retisch te bepalen.Een state-of-the-art Tuned MassDamper is toegepast in het 508 mhoge Taipei 101-gebouw, momen-teel het hoogste gebouw van dewereld (fig. 10 en 13). Het gebouwstaat in een regio waar veelvuldigtyfoons en aardbevingen voorko-men. Bovenin het gebouw hangteen stalen bal met een massa van800 ton. De bal is opgebouwd uit12,5 cm dikke platen en hangt aanstalen kabels. Met de lengte vande kabels kan de eigenfrequentievan het systeem worden ingesteld.Door het verschil in eigenfrequen-tie met dat van het gebouw,beweegt de slinger uit fase en metTabel 1|Overzicht van algemene waarden voor de dempingsratio's [9]type draagconstructie dempingratio Dhoogbouw (h>100m): min. gem. max.gewapend beton 0,010 0,015 0,020staal 0,007 0,010 0,013laagbouw (h~50m):gewapend beton 0,020 0,025 0,030staal 0,015 0,020 0,025Tabel 2|Overzicht additionele dempingsprincipes (passief en actief) [7]passieve demping actieve dempingmetaaldempers actieve verbanden systeemwrijvingsdempers actieve massa dempersvisco-elastische dempers actieve variabele stijfheid- of dempings-systeemviskeuze vloeistofdempers pulssysteemmassadempers a?rodynamische voorzieningenvloeistofdempersC o n s t r u c t i e & u i t v o e r i n gW indbelas tingcement 2006 136een andere snelheid. Als hetgebouw naar rechts beweegt,beweegt de demper naar links.Acht hydraulische veren, elk onge-veer 2 m lang, vangen de bewegingvan de stalen bal op en zetten dezeom in warmte.De Tuned Mass Damper van Taipei101 heeft 4 miljoen dollar gekosten reduceert de piekversnellingenop de topverdieping met 40%.K o s t e n - b a t e n a n a l y s eBeschreven mogelijkheden om hetdynamisch gedrag van een gebouwpositief te be?nvloeden hebben elkeen bepaalde effectiviteit en effi-ci?ntie. De constructeur zal veelalbeginnen met het verhogen van deconstructiestijfheid, door aanpas-sing van het systeem, toevoegingvan materiaal of wijziging van demateriaaleigenschappen. Indien ditonvoldoende of onmogelijk is, zalde duurdere oplossing van additio-nele demping worden aangewend.Daarbij neemt de relatieve effectivi-teit van toegevoegde demping inhet algemeen af naarmate deomvang van de dempingsmaatre-gelen toeneemt.De baten, bruikbaarheid en com-fort, zullen afnemen met het toe-nemend optreden van hinderlijketrillingen. De huurders van eengebouw zullen bij toenemendongemak het gebouw lager waar-deren. Het is echter geen eenvou-dige zaak de overwegingen naareen kosten-batenvraagstuk te ver-talen voor de gebouweigenaar ofinvesteerder.C o n c l u s i e sDe uniciteit die hoogbouw inhe-rent in zich heeft, vraagt telkensom een toegesneden antwoord vande constructief ontwerper. Mindertechnische randvoorwaarden alsbruikbaarheid, comfort en econo-mie zijn daarbij zeer bepalend. Hetdynamisch gedrag van de construc-tie moet in deze context geen vraagzijn, maar een resultaat, door deconstructeur aangestuurd geduren-de het gehele ontwerpproces. Hier-voor is kennis en kunde vereist vande verschillende parameters uit dewindloading-chain (zie fig. 2).Ten aanzien van de constructieverespons moeten de windbelastingen de constructie op een juistewijze, inzichtelijk en doelmatigworden gemodelleerd. Daarbij zalde betrouwbaarheid van de gevon-den resultaten evenredig toenemenmet de diepgang van elk ontwerp-stadium. Toch zullen ook in demeest geavanceerde modelleringenonzekerheden aanwezig zijn. Tenaanzien van het dynamisch gedraggaat het daarbij met name om demateriaaldemping, die geen onbe-langrijke invloed uitoefent op hetdynamisch gedrag. De voor de con-structie aan te houden dempings-waarde volgt weliswaar uit de NEN6702, maar verdient nog naderonderzoek. Metingen aan gebou-wen en laboratoriumonderzoekgeven een grote spreiding aan enbrengen de invloed van diversemechanismen aan het licht. Eennadere nuancering van de dem-pingswaarde zou een gewenste toe-komstige stap zijn. Daarbij zouvoor het materiaal beton de dem-pingswaarde afhankelijk kunnenworden gesteld van de optredendespanningen, de mate van scheur-vorming, de invloed van de beton-sterkte, aanwezige wapening, toe-slagmateriaal en voorspanning, deinvloed van voegen en/of prefabri-cage enz. Zo zou afhankelijk ofgekeken wordt naar extreme span-ningen, vervormingen of versnel-lingen een beter onderbouwdedempingswaarde kunnen wordenaangehouden, wat de betrouwbaar-heid van de resultaten ten goedekomt.Hoogbouw is dynamisch en kentvele uitdagingen. De kreet "Thesky is the limit" gaat echter alleenop zolang de andere grenzen daar-bij niet worden overschreden. nL i t e r a t u u r1. Davenport, A.G., The interac-tion of wind and structures.In: Engineering meteorology(red. E.J.Plate), Studies inWind Engineering and Indu-strial Aerodynamics, Vol.1,Elsevier, 1982.2. NEN 6702:2001, Belastingenen vervormingen, TGB 1990.NEN, december 2001.3. CUR-rapport 97-5, Dyna-misch gedrag van hogegebouwen. CUR, oktober1997.4. Holmes, J.D., Wind loadingof Structures. Spon Press,Londen, 2001.5. Oosterhout, G.P.C. van, enC.P.W. Geurts, Trillingen enhoogbouw: comfort en dem-ping. Cement 2001 nr. 2.6. www.Skyscraperpage.com.7. Soong, T.T. en M.C. Constan-tinou, Passive and ActiveStructural Vibration Controlin Civil Engineering. CISMNo.345, Springer-Verlag,Wenen/NewYork, 1994.8. www.monitoring.ca, Not AllVibrations Are Good Vibrati-ons. MSC Software Corporati-on, 2001.9. ISO 4354, Wind actions onstructures, 1997.13 | Tuned Mass Damper bijTaipei 101 [8]