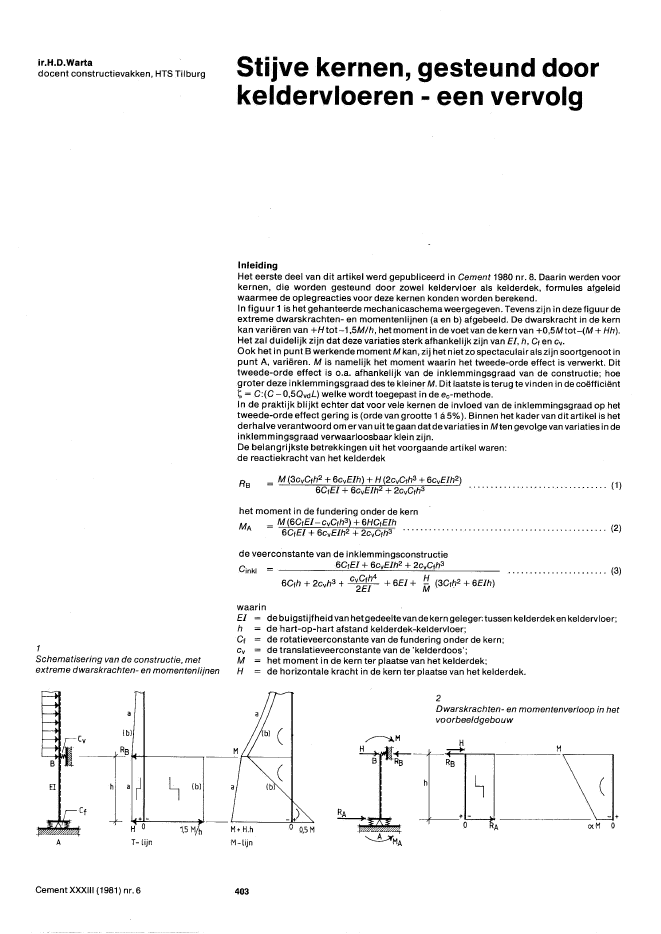
ir.H.D.Wartadocent constructievakken, HTS Tilburg Stijve kernen, gesteund doorkeldervloeren ?een vervolgInleidingHet eerste deel van dit artikel werd gepubliceerd in Cement 1980 nr. 8. Daarin werden voorkernen, die worden gesteund door zowel keldervloer als kelderdek, formules afgeleidwaarmee de oplegreacties voor deze kernen konden worden berekend.In figuur 1 is het gehanteerde mechanicaschema weergegeven. Tevens zijn in dezefiguurdeextreme dwarskrachten- en momentenlijnen (a en b) afgebeeld. De dwarskracht in de kernkan vari?ren van +Htot-1,5M/h, hetr;noment in de voet van de kern van +0,5Mtot-(M + Hh).Het zal duidelijk zijn dat deze variaties sterk afhankelijk zijn van EI, h, C, en cv.Ook het in punt B werkende moment M kan, zij het niet zo spectaculair als zijn soortgenoot inpunt A, vari?ren. M is namelijk het moment waarin het tweede-orde effect is verwerkt. Dittweede-orde effect is o.a. afhankelijk van de inklemmingsgraad van de constructie; hoegroter deze inklemmingsgraad des te kleiner M. Dit laatste is terug te vinden in de co?ffici?nt1;, = C:(C - 0,5QvdL) welke wordt toegepast in de ec-methode.In de praktijk blijkt echter dat voor vele kernen de invloed van de inklemmingsgraad op hettweede-orde effect gering is (orde van grootte 1 ? 5%). Binnen het kader van dit artikel is hetderhalve verantwoord om ervan uittegaan dat de variaties in Mten gevolge van variaties in deinklemmingsgraad verwaarloosbaar klein zijn.De belangrijkste betrekkingen uit het voorgaande artikel waren:de reactiekracht van het kelderdekRB _ M (3cvC,h2 +6cvEIh) + H(2cvC,h3+6cvEIh2)- 6C,EI + 6cvElh2 + 2cvC,h3 (1)het moment in de fundering onder de kernMA = M(6C,EI- cvC,h3) + 6HC,Elh (2)6C,EI + 6cvElh2 + 2cvC,h3 .de veerconstante van de inklemmingsconstructiee- - 6C,EI + 6cvElh2 + 2cvC,h3mkl - ?..?....?........?....? (3)6C,h + 2cvh3 + c2~t + 6EI + ~ (3C,h2 + 6Elh)1Schematisering van de constructie, metextreme dwarskrachten- en momentenlijnenwaarinEI de bu igstijfheid van hetgedeeltevan dekern geleger. tussen kelderdeken keldervloer;h de hart-op-hart afstandkelderdek-keldervloer;C, de rotatieveerconstante van de fundering onder de kern;Cv de translatieveerconstante van de 'kelderdoos';M het moment in de kern ter plaatse van het kelderdek;H de horizontale kracht in de kern ter plaatse van het kelderdek.2Dwarskrachten- en momentenverloop in hetvoorbeeldgebouwo 0,5 M((lbT-lijnaCv lb)I;;-1"lof-+-------------,1'~" ~ Ibl~HR'O'-----1-,5-M-?~h' - - M+ H.hM-lijnACement XXXIII (1981) nr. 6 403-+hl- - ,--'---C--,--- -'.~ - -Irr---II I iI I Ijl I- C~ ~cI I I 111lP"IL-~~-h+I I II . I. I4Kelderdoos met krachten U?t de kern3Doorsnede ?n langsr?cht?ng van hetvoorbeeldgebouwDe veerconstanten Cv en CfDe veerconstanten Cv en Cf zijn van grote invloed op met name de dwarskracht in kerngedeelteAB.In het eerste deel van dit artikel is dit onderzocht aan de hand van de invloed van cven Cfopdefactor a, de factor waarmee MA uitgedrukt kon worden in M(MA= aM). HetbleekdathoegroterCv des te kleiner a, enhoe groter Cf des te groter a (zie figuur 6a en ben tabel 1 uit deel I). Deinvloed van a op de dwarskracht kunnen we aflezen uit het volgende:I':..M M-aM MT = h = --h- = (1-a)T/ (4)In de inleiding is reeds geconstateerd dat variaties in de inklemmingsgraad in de meestegevallen slechts geringe variaties in het moment Mtotgevolg hadden. De invloed van Cv en Cfop het moment M mogen we verwaarlozen indien, in ec-rnethode termen, C : 0,5QvdL > 20,hetgeen in de praktijk ook meestal zo is.De grootte van de dwarskracht in de kern wordt dan in hoofdzaak bepaald door de factor a.Deze laatste iseen functievan meerderevariabelen, namelijkEI, h, M/h, cven Cf. Deeerste driegenoemde variabelen mogen we als gegeven beschouwen, daar ze ofwel met de huidigevoorschriften eenvoudig te bepalen zijn, ofwel direct volgen uit de door de architect ontwor-pen afmetingen. Voor Cv en Cf ligt dit heel anders; hiervoorstaan geen pasklare methodes terbeschikking. Ze zullen met een veilige benadering moeten worden bepaald. Een veiligemethode is di? benadering waarbij een zo klein mogelijke a wordt gevonden, omdat dan dedwarskracht wordt berekend op een zo grootmogelijke, dus veilige waarde. (In dit licht werdin heteerste deel ervoorgepleit om te rekenen met a = 0). Dit houdtvoorCv in dat gezocht dientte worden naar een benaderende berekening 'waarvan de j uitkomst zo grootmogelijk isen voor Cf een berekening waarvan de uitkomst zo klein mogelijk is. Natuurlijk dient bij ditalles de redelijkheid niet uit het oog te worden verloren.Benaderende berekening voor CvAan de hand van het voorbeeld uit het eerste deel zullen we een benaderende berekeninguitvoeren voor Cv. Daarbij gaan we uit van het in figuur 2 geschetste dwarskrachten- enmomentenverloop. In figuur 3 is een doorsnede gegeven van het betreffende gebouw. Deverbindingen tussen het kelderdek en de kern, respectievelijk de keldervloer en de kern zijnhierin geschematiseerd tot scharnieren. De afrnetingen zijn: lengte 60 rn, breedte 30 m,kelderhoogte 3,5 m, wand- en vloerdikte 0,25 m.De kracht op het kelderdek (Ug.4) wordt via dit dek afgevoerd naar de kelderwanden. Wegenshun geringere stijfheid in de beschouwde richting zal het aandeel van de kopwandenverwaarloosbaar zijn ten opzichtevan het aandeel der zijwanden. Via de zijwanden wordt debelasting dan afgevoerd naar de keldervloer. Te zamen met de kracht van de kern op dekeldervloer vormt dit dan de horizontale belasting van deze vloer.Hoe groot is nu de verplaatsing van punt B ten opzichte van punt A? In puntB werkt een krachtter grootte Rs en in punt A een kracht ter grootte RA= Rs - H. Vertalen we dit naar??nheidskrachtendanvindenweFs=1enFA=1-~.Nu is veelal het quoti?nt van Hen. RsRs verwaarloosbaar klein ten opzichte van de ??nheid (zo was bijvoorbeeld in deel I: H = 2300kN en Rs = 23728 kN, ofwel H/Rb = 2300/23728 = 0,097). Het is derhalve in dit voorbeeldverantwoord om te stellen dat FA = Fs = 1.De kracht Fs laten we, zoals in het voorafgaande reeds werd vermeld, volledig opnemen doorde zijwanden van de kelder. Perwand werkterzodoende een kracht FWand= 1f2, waarvanwordtaangenomen dat deze kracht gelijkmatig over de lengte van de wand verdeeld zal zijn.De verplaatsing van punt B kunnen we opgebouwd denken uit de verplaatsingsaandelen vanhet dek, de zijwanden, de vloer en de palen.Cement XXXIII (1981) nr.6 404Cement XXXIII (1981) nr. 6a. verplaatsingsaandeel dek:d k ht . "- l'b~ 'I: .1'b - V2Fb.1'b~ b _(1+f-l)'b_1,16bwars rac vervormmgu,-y' 12 - G 12 - d.e.G 12 - 4deG - 2Ede - 2EdeIk . "-1'. V2 Fs. V2e ~ e ~ enormaa rachtvervormmguN- 12 ~--A- - 8EA - 8Edbb. verplaatsingsaandeel zijwanden:dwarskrachtvervOrming?,=y.h=G'I: ?h= 2(1+1'). V2 Fs' h = 1,16hE de Edec. verplaatsingsaandeel vloer:Wegens de aanwe:i!:igheid van palen en poeren onder de vloer zal de vervorming van de vloergeringer zijn dan van hetdek. De mate waarin hangt o.a. af van wat men aan belastingafdrachtwil toekennen aan de palen. In het kadervan een veiligebenadering stellen we hetaandeel nul.d. verplaatsingsaandeel palen:?= Ct = lpcp = 2,8' 107 kNmiradCp = 0,5' 105 kN/mSubstituerenwenucv=0,82'107 kN/menCt=2,8'107 kNm/rad in a = CtCt + cvh2 'dan vinden we a = 0,22.ConclusieWegens het ontbreken van nauwkeurige handberekeningsmethoden voordeveerconstantenCv en Ct is het, in verband met de dwarskracht in de kern, raadzaam om uit te gaan vanongunstige waarden voor beide constanten. Het tussen kelderdek enkeldervloer gelegengedeelte van de kern wordt dan weliswaar op dwarskracht te zwaar berekend, doch dedaarvoor eventueel benodigde maatregelen zijn van dien aard, dat ze nauwelijks kostenver-hogend zullen zijn.405