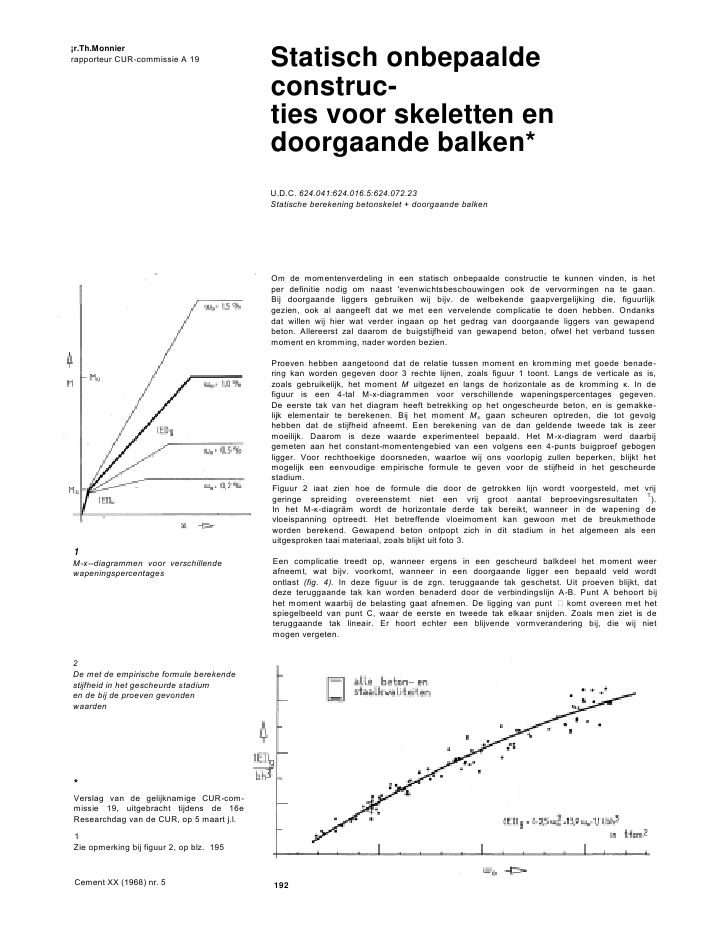
?r.Th.Monnierrapporteur CUR-commissie A 19 Statisch onbepaaldeconstruc-ties voor skeletten endoorgaande balken*U.D.C. 624.041:624.016.5:624.072.23Statische berekening betonskelet + doorgaande balken1M-x--diagrammen voor verschillendewapeningspercentagesOm de momentenverdeling in een statisch onbepaalde constructie te kunnen vinden, is hetper definitie nodig om naast 'evenwichtsbeschouwingen ook de vervormingen na te gaan.Bij doorgaande liggers gebruiken wij bijv. de welbekende gaapvergelijking die, figuurlijkgezien, ook al aangeeft dat we met een vervelende complicatie te doen hebben. Ondanksdat willen wij hier wat verder ingaan op het gedrag van doorgaande liggers van gewapendbeton. Allereerst zal daarom de buigstijfheid van gewapend beton, ofwel het verband tussenmoment en kromming, nader worden bezien.Proeven hebben aangetoond dat de relatie tussen moment en kromming met goede benade-ring kan worden gegeven door 3 rechte lijnen, zoals figuur 1 toont. Langs de verticale as is,zoals gebruikelijk, het moment M uitgezet en langs de horizontale as de kromming . In defiguur is een 4-tal -x-diagrammen voor verschillende wapeningspercentages gegeven.De eerste tak van het diagram heeft betrekking op het ongescheurde beton, en is gemakke-lijk elementair te berekenen. Bij het moment Ms gaan scheuren optreden, die tot gevolghebben dat de stijfheid afneemt. Een berekening van de dan geldende tweede tak is zeermoeilijk. Daarom is deze waarde experimenteel bepaald. Het M-x-diagram werd daarbijgemeten aan het constant-momentengebied van een volgens een 4-punts buigproef gebogenligger. Voor rechthoekige doorsneden, waartoe wij ons voorlopig zullen beperken, blijkt hetmogelijk een eenvoudige empirische formule te geven voor de stijfheid in het gescheurdestadium.Figuur 2 iaat zien hoe de formule die door de getrokken lijn wordt voorgesteld, met vrijgeringe spreiding overeenstemt niet een vrij groot aantal beproevingsresultaten T).In het --diagr?m wordt de horizontale derde tak bereikt, wanneer in de wapening devloeispanning optreedt. Het betreffende vloeimoment kan gewoon met de breukmethodeworden berekend. Gewapend beton ontpopt zich in dit stadium in het algemeen als eenuitgesproken taai materiaal, zoals blijkt uit foto 3.Een complicatie treedt op, wanneer ergens in een gescheurd balkdeel het moment weerafneemt, wat bijv. voorkomt, wanneer in een doorgaande ligger een bepaald veld wordtontlast (fig. 4). In deze figuur is de zgn. teruggaande tak geschetst. Uit proeven blijkt, datdeze teruggaande tak kan worden benaderd door de verbindingslijn A-B. Punt A behoort bijhet moment waarbij de belasting gaat afnemen. De ligging van punt komt overeen met hetspiegelbeeld van punt C, waar de eerste en tweede tak elkaar snijden. Zoals men ziet is deteruggaande tak lineair. Er hoort echter een blijvende vormverandering bij, die wij nietmogen vergeten.2De met de empirische formule berekendestijfheid in het gescheurde stadiumen de bij de proeven gevondenwaarden*Verslag van de gelijknamige CUR-com-missie 19, uitgebracht tijdens de 16eResearchdag van de CUR, op 5 maart j.l.1Zie opmerking bij figuur 2, op blz. 195Cement XX (1968) nr. 5 1923Gewapend beton ontpopt zich in ditstadium in het algemeen als eenuitgesproken taai materiaalHet is ook interessant het moment eens van teken te laten veranderen. Wij zien dan, zoalsblijkt uit fig. 5a, dat na het optreden van scheuren in de oorspronkelijke drukzone, de stijf-heid in feite dezelfde is als wanneer het een eerste belasting in die richting zou zijn. Alshet moment daarna de oorspronkelijke waarde weer bereikt, is in het M-x-diagram een lusdoorlopen, zoals is aangegeven in fig. 5b.Fig. 6a toont dat na overschrijding van het vloeimoment, de teruggaande tak eenzelfde rich-ting houdt; de stijfheid daarlangs verandert dus niet en alle plastische vorming is blijvend.Uit fig. 6b blijkt dat bij terugkeer naar de oorspronkelijke situatie er weer een lus wordtdoorlopen, die met genummerde pijlen is aangegeven.Wij zullen de complicatie, die bij een tekenwisseling van moment optreedt, maar even ver-geten. Met de drie takken van het oorspronkelijke --diagram in gedachten, zullen wijeens nagaan wat er gebeurt wanneer de belasting op een doorgaande ligger langzaamwordt opgevoerd. Dit is voorgesteld in het diagram van fig. 7 (zie blz. 194).Langs de verticale as staat de belasting en in horizontale richting zijn de momenten Muitgezet. De beide dun getrokken lijnen geven de elastische momenten: links het veld-moment en rechts het steunpuntsmoment. De dikkere lijnen behoren bij de werkelijk op-tredende momenten! Bij het opvoeren van de belasting blijft de ligger aanvankelijk onge-scheurd. Er is geen enkele reden waarom de momentenverdeling nu zou afwijken van deelastische waarden. In het diagram vallen de betreffende lijnen dan ook samen.Zoals reeds vermeld, heeft scheurvorming een vermindering van de stijfheid tot gevolg.Bereikt het steunpuntsmoment als eerste het scheurmoment Ms, dan gebeurt er iets. Ertreedt een wijziging van de momentenverdeling op. Wij spreken dan van een herverdelingvan momenten. Denken wij weer even aan de gaapvergelijking, dan wordt duidelijk dat metde slappere liggereinden bij het steunpunt, de fictieve gaping gemakkelijker, dat wilzeggen met een kleiner steunpuntsmoment, kan worden gesloten. We zien het steunpunts-moment bij verdere belastingverhoging dan ook minder snel toenemen.Cement XX (1968) nr. 5 1938Bezwijkmechanisme bij doorgaande balkOp grond van het vereiste evenwicht wordt het veldmoment nu relatief groter. Het scheurenvan het veld hierna heeft uiteraard een compenserend effect. De momentenverhoudinghangt geheel af van de dan geldende stijfheidsverhouding tussen het gebied van de posi-tieve en het gebied van de negatieve momenten.In het diagram wordt boven het steunpunt het eerst het vloeimoment bereikt. Bij verderopvoeren van de belasting kan het moment daar niet meer toenemen. Er is nu een zoge-noemd plastisch scharnier gevormd. In deze situatie moeten de doorsneden in het veldall??n de vereiste toename van het moment leveren, waardoor het veldmoment dus sneltoeneemt. Gaat ten slotte ook de veldwapening vloeien, dan ontstaat het in fig. 7 ge-schetste bezwijkmechanisme. De belasting kan nu niet verder worden opgevoerd; de con-structie zakt immers al langzaam ineeen, en breekt waar de rotatie-capaciteit van een plas-tisch scharnier wordt bereikt. Foto 8 toont zo'n bezwijkmechanisme aan een modelbalk.Uitgaande van het bezwijkmechanisme kan de constructie ook worden berekend, en welvolgens de zgn. bezwijkanalyse. Zoals in het voorgaande duidelijk werd, is het dus hele-maal niet nodig dat het vloeimoment in de kritieke doorsneden gelijktijdig wordt bereikt. Ermag best ergens vloeien optreden, v??rdat van een mechanisme kan worden gesproken. Inhet algemeen kunnen wij bij het bepalen van de draagkracht dan ook gewoon uitgaan van eenkrachtenverdeling, waarbij het vereiste evenwicht mogelijk is; met andere woorden, met eenbepaalde bezwijkbelasting in gedachten, kan de verhouding tussen veldwapening en steun-puntswapening willekeurig worden gekozen. Welke verhouding ook gekozen wordt, aan deveiligheid van de ligger wordt hierdoor g??n afbreuk gedaan.Lang v??rdat het bezwijkmechanisme ontstaat, moet echter ook al de nodige aandacht aanhet gedrag van de constructie worden besteed. Met name in het gebruiksstadium mag nochde grootste scheurwijdte, noch de doorbuiging de toelaatbare waarde gaan overschrijden.Ongetwijfeld betekenen deze beide facetten een beperking van de grote vrijheid in dewapeningskeuze, die we zojuist hebben ontdekt. Over de waarde van die beperking isechter weinig bekend. Commissie A 19 heeft zich daarom ten doel gesteld hierover denodige kennis te gaan vergaren en aldus te proberen een nuttige schaduw te zijn voor deCEB-commissie 'Structures Hyperstatiques'.Om de in het voorgaande gegeven uiteenzetting aan experimenten te kunnen toetsen enmet het verzamelen van gegevens te beginnen, zijn kortgeleden 4 doorgaande liggers be-proefd. De eerste proef betrof een ligger, waarin de wapening precies was aangepast aande elastische momenten. Aangetoond werd dat de re?le momentenverdeling overeenkomtmet de elastische, zoals uit fig. 9 blijkt. Hierin zijn weer de belasting en de momenten tegenelkaar uitgezet.Figuur 9 en 10Cement XX (1968) nr. 519411Stadie tijdens ??n cyclus van hetlastwisselschemaZoals we zien, liggen de meetresultaten (dat zijn de punten) praktisch op de lijnen die deelastische momentenverdeling geven. Het stadium waarin alleen scheuren boven het steun-punt voorkomen, toont een geringe afwijking. Het vloeien van de wapening trad in de proefdan ook vrijwel gelijktijdig boven het steunpunt en in het veld op, bij een belasting dienagenoeg gelijk was aan de berekende bezwijkbelasting. Voor deze balk vormen de GBV-eisen wat betreft de grootste scheurwijdte en de doorbuiging in het gebruiksstadium geenenkel probleem.In de praktijk bestaat echter grote belangstelling voor de mogelijkheden die er zijn om desteunpuntswapening te verminderen en in plaats daarvan meer wapening in de velden teleggen. Daarom is deze werkwijze ook in de overige proefbalken toegepast. Uit dezeproeven blijkt, dat de steunpuntswapening die elastisch gezien nodig is, met ca. 40% kanworden verminderd. D?n treedt in het gebruiksstadium de grootste toelaatbare scheurwijdteboven het steunpunt op. Fig. 10 geeft een indruk van de vrij aanzienlijke herverdeling vanmomenten, die erbij plaatsvindt. De doorbuiging blijft echter ruimschoots aan de GBV-eisenvoldoen.In het laatste geval wordt de situatie, gelet op de grootste scheurwijdte, echter in aanzienlijkemate ongunstiger, wanneer de belasting wat wordt gewisseld. In fig. 11 is ??n cyclus van hetlastwisselschema gegeven. De liggervelden worden daarbij ook afzonderlijk belast. Hoewelhierdoor de vervormingen dus sterk toenemen, blijken deze lastwisselingen gelukkig g??ninvloed te hebben op de herverdeling van momenten wanneer na een aantal van deze cyclus-sen zich een stationaire toestand heeft ingesteld.Met het -x-diagram als gegeven in fig. 1, kan ook de re?le momentenverdeling wordenberekend. Bij het IBBC-TNO is daarvoor een rekenprogramma voor de computer gemaakt.Hier blijkt echter dat het berekende steunpuntsmoment ten opzichte van de meetresultatensteeds aan de hoge kant ligt. Bij het middensteunpunt van de beproefde balken wordt dekromming door de daar optredende dwarskracht dermate discontinu, hetgeen ook uit de rek-metingen blijkt, dat het M-x-diagram, bepaald aan een constant momentengebied, er zondercorrecties g??n goede maat meer voor is.De commissie zoekt hier nu een oplossing voor, met de bedoeling veel gegevens rekenen-derwijze te verkrijgen, waardoor het experimenteel onderzoek beperkt kan blijven.Het werk van commissie A 19, en dat is ongetwijfeld ook bij andere commissies het geval,raakt allerlei technische problemen die tot voor kort afzonderlijk werden behandeld. Dit is bijvoorbeeld het geval met: vervorming van gewapend beton, scheurvorming, dwarskrachtproblemen, rotatiecapaciteit van plastische scharnieren, enz.Dit is duidelijk een tweede fase in het CUR- en CEB-werk. Naast extra moeilijkheden heeftdit toch ook een zonnige zijde, waaraan normaal uitdrukking wordt gegeven door te zeg-gen dat het 'nu pas leuk wordt'! In deze stemming gaat commissie A 19 voort, met hetdoel voor ogen zo snel mogelijk met concrete aanbevelingen te komen.Opmerking bij figuur 2 (blz. 192) De getekende kromme is berekend als degene, die ten opzichte van de beschikbare meet-resultaten de kleinste gemiddelde afwijking geeft. De bijbehorende uitdrukking wordt in hetdoor de commissie gebruikte computerprogramma zonder bezwaar toegepast. Deze is echtergeenszins bedoeld als een eindprodukt.In de discussie op de CUR-dag bleek voor de empirische uitdrukking veel belangstelling tebestaan. Voor praktisch gebruik zou men ter wille van de eenvoud, wel een wat grotereafwijking ten opzichte van deze verzameling meetresultaten willen accepteren. In dat gevalkan voor wapeningspercentages tussen 0,2% en bijv. 1,5% goed gebruik worden gemaaktvan de uitdrukking: (EI)g = 10 0 . b . h3tfcm2. De bijbehorende rechte is in fig. 2a geschetst.Introduceert men in deze uitdrukking:A = de hoeveelheid trekwapening =--? ' '--; enEa = de elasticiteitsmodulus van staal = 2,1 X 10skgf/cm2,dan wordt de vergelijking: (EI)g = 0,48 Ea . A . h2 0,5 E . A . h2kgfcm2Figuur 2aCement XX (1968) nr. 5 195