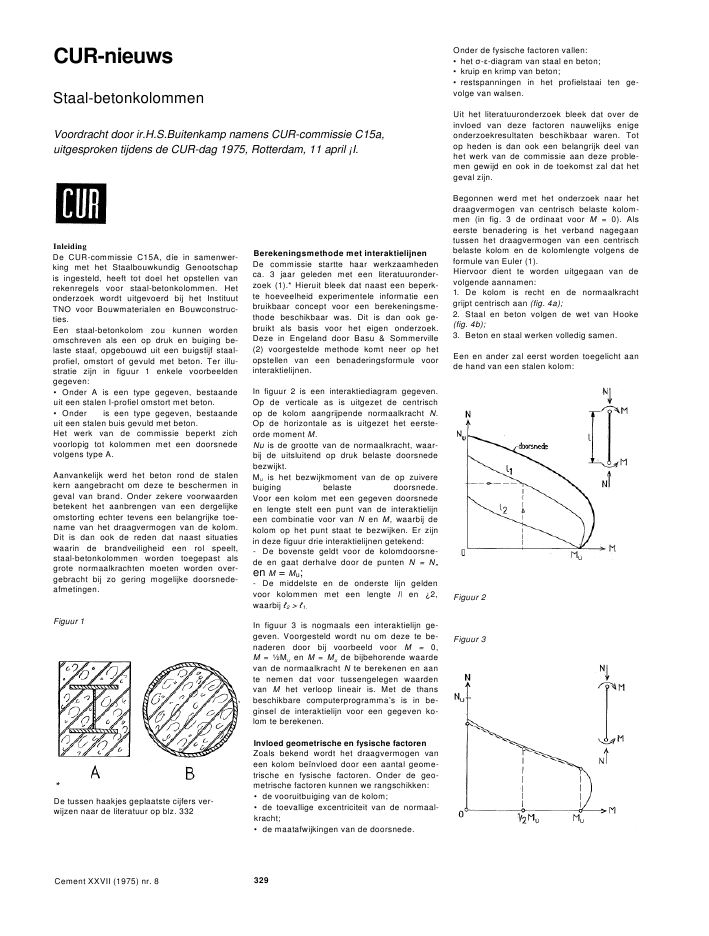
InleidingDe CUR-commissie C15A, d?e in samenwer-king met het Staalbouwkundig Genootschapis ingesteld, heeft tot doel het opstellen vanrekenregels voor staal-betonkolommen. Hetonderzoek wordt uitgevoerd bij het InstituutTNO voor Bouwmaterialen en Bouwconstruc-ties.Een staal-betonkolom zou kunnen wordenomschreven als een op druk en buiging be-laste staaf, opgebouwd uit een buigstijf staal-profiel, omstort of gevuld met beton. Ter illu-stratie zijn in figuur 1 enkele voorbeeldengegeven:? Onder A is een type gegeven, bestaandeuit een stalen I-profiel omstort met beton.? Onder is een type gegeven, bestaandeuit een stalen buis gevuld met beton.Het werk van de commissie beperkt zichvoorlopig tot kolommen met een doorsnedevolgens type A.Aanvankelijk werd het beton rond de stalenkern aangebracht om deze te beschermen ingeval van brand. Onder zekere voorwaardenbetekent het aanbrengen van een dergelijkeomstorting echter tevens een belangrijke toe-name van het draagvermogen van de kolom.Dit is dan ook de reden dat naast situatieswaarin de brandveiligheid een rol speelt,staal-betonkolommen worden toegepast alsgrote normaalkrachten moeten worden over-gebracht bij zo gering mogelijke doorsnede-afmetingen.Figuur 1Berekeningsmethode met interaktielijnenDe commissie startte haar werkzaamhedenca. 3 jaar geleden met een literatuuronder-zoek (1).* Hieruit bleek dat naast een beperk-te hoeveelheid experimentele informatie eenbruikbaar concept voor een berekeningsme-thode beschikbaar was. Dit is dan ook ge-bruikt als basis voor het eigen onderzoek.Deze in Engeland door Basu & Sommerville(2) voorgestelde methode komt neer op hetopstellen van een benaderingsformule voorinteraktielijnen.In figuur 2 is een interaktiediagram gegeven.Op de verticale as is uitgezet de centrischop de kolom aangrijpende normaalkracht N.Op de horizontale as is uitgezet het eerste-orde moment M.Nu is de grootte van de normaalkracht, waar-bij de uitsluitend op druk belaste doorsnedebezwijkt.Mu is het bezwijkmoment van de op zuiverebuiging belaste doorsnede.Voor een kolom met een gegeven doorsnedeen lengte stelt een punt van de interaktielijneen combinatie voor van N en M, waarbij dekolom op het punt staat te bezwijken. Er zijnin deze figuur drie interaktielijnen getekend:- De bovenste geldt voor de kolomdoorsne-de en gaat derhalve door de punten N = N,,en M = Mu;- De middelste en de onderste lijn geldenvoor kolommen met een lengte l\ en ?2,waarbij 2 > 1.In figuur 3 is nogmaals een interaktielijn ge-geven. Voorgesteld wordt nu om deze te be-naderen door bij voorbeeld voor M = 0,M = ?Mu en M = Mu de bijbehorende waardevan de normaalkracht N te berekenen en aante nemen dat voor tussengelegen waardenvan M het verloop lineair is. Met de thansbeschikbare computerprogramma's is in be-ginsel de interaktielijn voor een gegeven ko-lom te berekenen.Invloed geometrische en fysische factorenZoals bekend wordt het draagvermogen vaneen kolom be?nvloed door een aantal geome-trische en fysische factoren. Onder de geo-metrische factoren kunnen we rangschikken:? de vooruitbuiging van de kolom;? de toevallige excentriciteit van de normaal-kracht;? de maatafwijkingen van de doorsnede.Onder de fysische factoren vallen:CUR-nieuws ? het --diagram van staal en beton;? kruip en krimp van beton;? restspanningen in het profielstaai ten ge-volge van walsen.Staal-betonkolommenUit het literatuuronderzoek bleek dat over deinvloed van deze factoren nauwelijks enigeonderzoekresultaten beschikbaar waren. Totop heden is dan ook een belangrijk deel vanhet werk van de commissie aan deze proble-men gewijd en ook in de toekomst zal dat hetgeval zijn.Voordracht door ir.H.S.Buitenkamp namens CUR-commissie C15a,uitgesproken tijdens de CUR-dag 1975, Rotterdam, 11 april ?I.Begonnen werd met het onderzoek naar hetdraagvermogen van centrisch belaste kolom-men (in fig. 3 de ordinaat voor M = 0). Alseerste benadering is het verband nagegaantussen het draagvermogen van een centrischbelaste kolom en de kolomlengte volgens deformule van Euler (1).Hiervoor dient te worden uitgegaan van devolgende aannamen:1. De kolom is recht en de normaalkrachtgrijpt centrisch aan (fig. 4a);2. Staal en beton volgen de wet van Hooke(fig. 4b);3. Beton en staal werken volledig samen.Een en ander zal eerst worden toegelicht aande hand van een stalen kolom:Figuur 2Figuur 3*De tussen haakjes geplaatste cijfers ver-wijzen naar de literatuur op blz. 332Cement XXVII (1975) nr. 8 329in figuur 5a is het verband uitgezet tussen denormaalkracht op de doorsnede en de stuik. Als we uitgaan van het eerder genoemdebilineaire --diagram, dan is het --verloopeveneens bilineair. In figuur 5b is het verbanduitgezet tussen de EId van de kolom en destuik . Tot aan de vloeirek is E en dus deEI constant. Voor grotere waarden van isde buigstijfheid nul. De oorzaak van de dis-continu?teit is het bilineair verloop van het--diagram.KnikkrommeMet behulp van deze beide figuren kan deknikkromme worden toegelicht (fig. 5c):Voor kolommen die uitknikken bij een krachtkleiner dan Nu, geldt de formule van Eulerwaarbij voor de buigstijfheid van de door-snede de waarde EIa uit figuur 5b wordt in-gevuld. Bij het bereiken van de vloeigrens(Nu) kan niet gesproken worden van een buig-stijfheid. De formule van Euler geldt dan nietmeer. Voor kolommen met een lengte kleinerdan de aangegeven waarde ke geldt dat debezwijkbelasting gelijk is aan Nu.Op analoge wijze kan nu de knikkromme voorstaal-betonkolommen met een gegeven door-snede worden bepaald (fig. 6):In figuur 6a is weer het verband uitgezet tus-sen N en . Omdat de waarde van waarbijhet staal vloeit, niet gelijk is aan de waarde van waarbij het beton 'vloeit', vinden we nu tweeknikpunten. Hier is aangenomen dat de vloei-stuik van het staal (ae) kleiner is dan die vanhet beton ( ). In figuur 6b is het verbandtussen de El en getekend. Zolang geen vande materialen vloeit is de EI van de doorsne-de de som van de EIs van beton en staal.Voor ae < < be vloeit het staal en levertgeen bijdrage meer aan de buigstijfheid. Deresterende buigstijfheid is dan gelijk aan deEI van beton (de afname is discontinu).Voor > be 'vloeit' het beton eveneens. Debezwijkbelasting van een kolom is in dat ge-val gelijk aan de vloeikracht van de door-snede.Op grond van deze gegevens kan nu de knik-kromme worden toegelicht (fig. 6c):Voor kolommen met een lengte zodanig datN < Npu, geldt dat voor de buigstijfheid EIdin de formule van Euler m?et worden aange-houden EIa + EIb. Zoals uit het voorgaandeis gebleken, zal voor kolommen met een klei-nere lengte de Eulerse knikkracht groter kun-nen zijn dan de Ngu. We hebben gezien dat indat geval nog uitsluitend de EI van het betonoverblijft. Dit ingevuld in de formule vanEuler leidt tot de tak, aangegeven met EIb.Het overgangsgebied tussen de beide krom-men wordt gevormd door een horizontaaltraject.NB: Het blijkt dat over een klein gebied debezwijkbelasting onafhankelijk is van dekolomlengte.Resteert nog het deel van de kromme datgeldt voor zeer korte kolommen. Deze kolom-men bezwijken bij een belasting, gelijk aan devloeikracht van de doorsnede Nu.Proeven naar verloop knikkrommeMede gezien de uitgebreide discussies hier-over in onze commissie en het gebrek aanexperimentele informatie, werd besloten ditverloop door middel van proeven te verifi?ren(3). We hebben ons hierbij gerealiseerd dathet geen eenvoudige zaak is om het verloopvan een Eulerse knikkromme door middel vanproeven aan te tonen. Beproefd werden 10kolommen op modelschaal. De doorsnede-afmetingen zijn in figuur 7 gegeven, de ko-lomlengten bedroegen 400 - 600 - 800 -1000 -1200-1400 mm. Daarnaast werd een aantalzeer korte kolommen gedrukt, om tezamenmet de resultaten van prisma-drukproevengegevens te verkrijgen over de --diagram-men van het staal en het beton.De materiaaleigenschappen zijn gegeven infiguur 8. Voor staal kon een bilineair diagramworden aangehouden, voor beton een para-bolisch diagram. De op grond van deze ma-teriaalgegevens berekende knikkromme ende proefresultaten zijn gegeven in figuur 9a.De berekening van deze kromme verloopt alshiervoor is uiteengezet, echter met dit ver-schil dat we hier te maken hebben met eenparabolisch --diagram van beton. Het isdan gebruikelijk om in plaats van de elastici-teitsmodulus de tangentmodulus aan te hou-den. Het effect van het kromlijnig diagramvoor beton komt tot uiting in:1. een minder stijl verlopende elastische tak;2. nadat het staal gevloeid is, een vloeiendverlopende kromme tot aan Nu.Cement XXVII (1975) nr. 8 330Bij de beproeving van de kolommen werdenbehalve de grootte van de belasting de span-ningsverdeling en de uitwijking halverwegede kolomlengte gemeten.De resultaten konden dank zij de nauwkeurigbepaalde materiaaleigenschappen wordengeanalyseerd met behulp van het door DeGroot bij het IBBC ontwikkelde computer-programma SAMKO (4). De wijze waaropdeze analyse is uitgevoerd, zal worden ge?llu-streerd aan de hand van de kolommen 7 en 8.De bezwijkbelasting van kolom 8 bleek over-een te komen met de Eulerse knikkracht. Debezwijkbelasting van kolom 7 bleek aanzien-lijk kleiner te zijn. Berekend is hoe groot devooruitbuiging 0 van kolom 7 zou moetenzijn opdat de berekende bezwijkbelasting ge-lijk is aan het proefresultaat.Deze fictieve vooruitbuiging bedroeg 0,5 mm{fig.9b). Uitgaande van deze vooruitbuigingis het verband berekend tussen de belastingen de uitbuiging van de kolom. Dit bleekovereen te komen met het proefresultaat.Conclusie:De veronderstelde vooruitbuiging van 0,5 mmblijkt een redelijke benadering te geven vande imperfecties van kolom 7.Het last-uitbuigingsdiagram van kolom 7 en 8is gegeven in figuur 10. Met uitzondering vankolom 9 bleek ook voor de overige kolom-men het rekenresultaat goed in overeenstem-ming met het proefresultaat en kon op dewijze als hiervoor is beschreven een goedeschatting worden gemaakt van de fictievevooruitbuiging 0.Het feit dat voor kolom 9 een bezwijkbelas-ting werd gevonden hoger dan volgt uit deknikkromme voor een ideaal rechte kolom,zou kunnen worden verklaard door het gelijk-tijdig optreden van een vooruitbuiging en eenexcentriciteit van de normaalkracht, waarbijFiguur 9de uitbuiging ten gevolge van de belastingtegengesteld is aan de initi?le vervorming vande kolom. Een dergelijk verschijnsel is bijv,ook waargenomen bij de beproeving vanslanke stalen kolommen.De conclusies die uit dit modelonderzoek zijngetrokken waren de volgende:1. De proefresultaten bevestigden de theorievoor de ideaal rechte kolom.2. Als het materiaalgedrag bekend is, blijkthet beschikbare computerprogramma de be-zwijkbelasting en de vervorming goed te be-rekenen.Invloed kruip op knikkrommeTot dusver is nog niet gesproken over heteffect van kruip. Voor de ideaal rechte kolomis de invloed kwalitatief echter eenvoudigweer te geven. Als gevolg van kruip zal ineen op druk belaste staal-betondoorsnedeeen herverdeling van spanningen optreden.Het effect hiervan is weergegeven in figuur11b.Als op de doorsnede een drukkracht N wordtaangebracht dan is op t = 0 de verdeling vanN over het staal en beton als is aangegevenmet Na0 en N 0. Als gevolg van kruip zal dekracht in het beton afnemen en die in hetstaal toenemen. Op t = oo ?s de krachtsver-deling stabiel geworden. De kracht in hetstaal bedraagt dan Na, die ?n het beton N .Men kan zich voorstellen dat voor een kolommet lengte 1, belast met een kracht iets klei-ner dan Npuo, het staal ten gevolge van kruipzal gaan vloeien. Op grond van de dan reste-rende buigstijfheid kan de kolom maximaalde met een accolade aangegeven kracht op-nemen (fig. 10 ).Bij een gegeven kruipgedrag van beton is teberekenen bij welke kracht N het staal opt= net vloeit. Deze kracht is in figuur 10aaangegeven met /VpUoo. Voor het verloop vande knikkromme betekent dit nu dat, rekeninghoudend met kruip, het horizontale deel vanFiguur 10de kromme behorende bij NpUo daalt tot NpUoo.Een tweede correctie die moet worden aan-gebracht, vloeit voort uit het feit dat een ho-ge betondrukspanning, aangebracht op t = 0,aanleiding kan zijn tot bezwijken op een latertijdstip. Algemeen wordt aangenomen dat, alsde betondrukspanning op = 0 kleiner is dan75-80% van de korte-duur sterkte dit effectniet optreedt. Dit houdt dus in, dat de vloei-kracht van de doorsnede aangegeven met/VUo moet worden gereduceerd tot NUoo.Samenvattend is in figuur 10 met een getrok-ken lijn de knikkromme aangegeven voor eenkortstondige belastingproef. Met een stippel-lijn is de knikkromme aangegeven voor debelasting die op = 0 wordt aangebracht enwaarbij de kolom op t = oo op het punt vanCement XXVII (1975) nr. 8 331bezwijken staat. Uit het voorgaande volgt te-vens dat althans voor een ideaal rechte ko-lom het in rekening brengen van kruip doormiddel van een reductie van de elasticiteits-modulus van beton, zoals bijv. in de huidigebetonvoorschriften wordt gegeven, in princi-pe niet juist is.Verdere onderzoekingenIk kom nu aan een aantal onderwerpen waar-over nog weinig concreet onderzoekresultaatbeschikbaar is, maar waarover in onze com-missie reeds uitgebreid van gedachten is ge-wisseld. Het leek ons juist onze idee?n in hetkader van deze rapportage naar voren tebrengen.Het eerste onderwerp betreft wederom de in-vloed van kruip. Kwalitatief is deze invloedvoor een ideaal rechte, centrisch belastekol om reeds aangegeven. In de praktijk iseen kolom zoals reeds gezegd niet recht,maar bezit een vooruitbuiging. Bij het aan-brengen van een belasting zal deze uitbuigingwat groter worden. Als gevolg van kruip zalin de loop van de tijd de uitbuiging nog ver-der toenemen.Om het effect van kruip op het gedrag vaneen staal-betonkolom met vooruitbuiging tebestuderen, heeft De Groot het eerder ge-noemde computerprogramma SAMKO uitge-breid (5,6). Dit programma dat nu onder denaam KRUKO door het leven gaat, biedt onsde mogelijkheid om de bezwijkbelasting vaneen kolom te berekenen, waarbij naast degeometrie en het kortstondig materiaalgedragde volgende factoren worden ingevoerd:1. de belastinghistorie;2. een kruipfunctie + een tijdsafhankelijke re-ductie van de betondruksterkte.Dat de invloed van de belastinghistorie be-langrijk kan zijn, kan worden toegelicht metbehulp van figuur 12. Als een kolom met eenvooruitbuiging aan een kortstondige belas-tingproef wordt onderworpen, wordt bijv. eenbezwijkbelasting gevonden als aangegevenmet No. Met behulp van KRUKO kan de be-lasting N worden berekend die op t = 0wordt aangebracht en waarbij de kolom opt = oo op het punt staat te bezwijken. Dezebelastinghistorie is in figuur 12 aangegeven.In het gebruiksstadium zal de op t = 0 aan tebrengen belasting uit veiligheidsoverwegin-gen echter kleiner zijn.Blijft deze gebruiksbelasting gehandhaafd totf = oo en wordt deze vervolgens kortstondigopgevoerd tot aan bezwijken van de kolom,dan wordt een bezwijkbelasting N gevondendie ligt tussen de beide voorgaande. De ge-hanteerde veiligheidsmarge is dus kennelijkwat groter. De invloed van de belastinghisto-rie zoals hiervoor is toegelicht, wordt momen-teel bestudeerd.Ten slotte wil ik nog ingaan op het probleemvan de centrisch belaste kolommen, rekeninghoudend met de voorkomende imperfecties.De wijze waarop dit deel van het onderzoekwordt aangepakt, kan worden toegelicht aande hand van het voorbeeld'uit figuur 13.Getekend is een kolom met lengte l en be-last door een normaalkracht N. Eenvoudig-heidshalve wordt aangenomen dat de groottevan de bezwijkbelasting Nu uitsluitend af-hangt van de grootte van de doorsnede-afme-tingen fa en h. In de praktijk zullen echtermaatafwijkingen optreden. Zowel de parame-ter fa als h heeft een zekere kansverdeling.De grootte van Nu kan nu een groot aantalmalen worden berekend, waarbij iedere keerwillekeurig uit de verdelingen fa en h eenwaarde wordt gekozen. Het resultaat is eenkansverdeling van de bezwijkbelasting vande kolom.In werkelijkheid is het probleem veel gecom-pliceerder. Het aantal parameters is uiteraardaanzienlijk groter dan in dit voorbeeld en nietaltijd is van een parameter de kansdichtheids-functie bekend. Omdat het hier gaat overstaal-betonkolommen kan echter gebruik ge-maakt worden van de resultaten van een on-derzoek, dat door Strating en Vos bij hetStevin-laboratorium is uitgevoerd en dat on-der meer in Heron is gepubliceerd (7). Hunonderzoek betrof het draagvermogen vancentrisch belaste stalen kolommen, uitgaandevan een statische verdeling voor iedere para-meter die dit draagvermogen wezenlijk be-?nvloedt. De resultaten van dit onderzoek zijnvergeleken met de CEAM-kromme (fig. 14).Deze kromme is gebaseerd op een zeergroot aantal proefresultaten en geeft de knik-spanning voor stalen walsprofielen met eenonderschrijdingskans van enkele procenten.De overeenstemming van het door Stratingen Vos gevoerde onderzoek en deze experi-menteel bepaalde kromme blijkt uitstekendte zijn.Literatuur1. Ir.H.S.Buitenkamp: 'Inleidend onderzoeknaar het draagvermogen van staal-betonko-lommen', IBBC-TNO rapport BI-72-60.2. A.K.Basu, W.Sommerville: 'Derivation offormulae for the design of rectangular com-posite columns', Proc. ICE - Supplementaryvolume 1969 - Paper 7206 S.3. Ir.H.S.Buitenkamp: 'Modelproeven cen-trisch belaste staal-betonkolommen', IBBC-TNO rapport BI-74-41.4. Ir.A.K. de Groot: 'Korte beschrijving vanhet programma SAMKO ter berekening vansamengestelde kolommen', IBBC-TNO rap-port BI-74-7.5. Ir.A.K. de Groot: 'Berekening van een ko-lom waarbij de invloed van kruip op vezel-niveau wordt ingevoerd', IBBC-TNO rapportBI-74-81.6. Ir.A.K. de Groot: 'Beschrijving van het pro-gramma KRUKO voor de berekening vanstaal-betonkolommen, rekening houdend methet effect van kruip', IBBC-TNO rapport Bl-74-82.7. John Strating en Han Vos (Stevin-lab):'Computer simulation of the ECCS bucklingcurve using a Monte-Carlo method', Heron,Volume 19, 1973, no. 2.Cement XXVII (1975) nr. 8 332