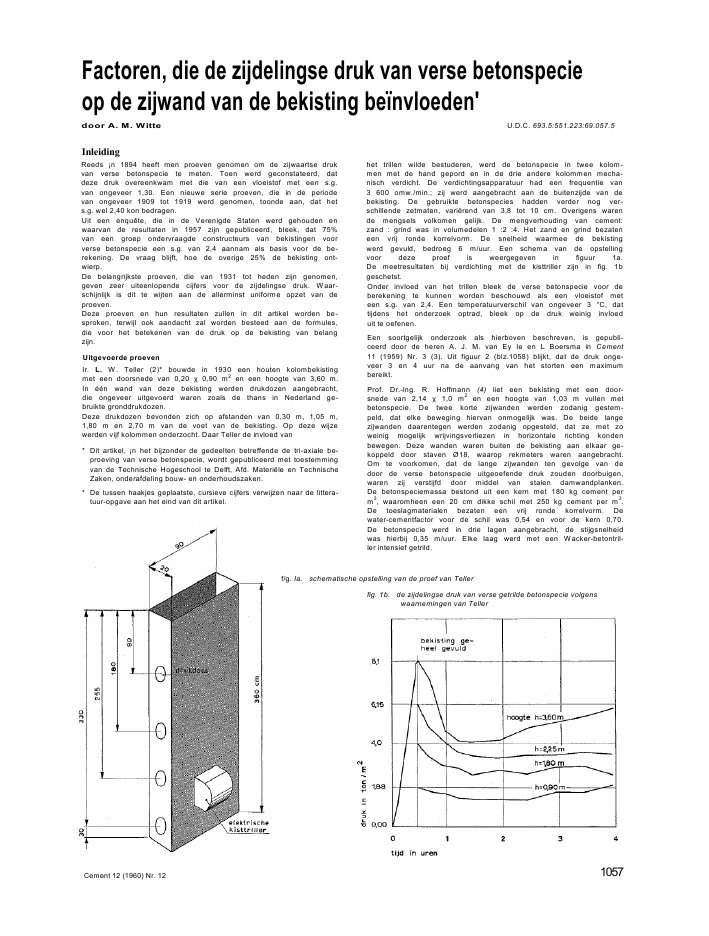
Factoren, die de zijdelingse druk van verse betonspecieop de zijwand van de bekisting be?nvloeden'door A. M. Witte U.D.C. 693.5:551.223:69.057.5InleidingReeds ?n 1894 heeft men proeven genomen om de zijwaartse drukvan verse betonspecie te meten. Toen werd geconstateerd, datdeze druk overeenkwam met die van een vloeistof met een s.g.van ongeveer 1,30. Een nieuwe serie proeven, die in de periodevan ongeveer 1909 tot 1919 werd genomen, toonde aan, dat hets.g. wel 2,40 kon bedragen.Uit een enqu?te, die in de Verenigde Staten werd gehouden enwaarvan de resultaten in 1957 zijn gepubliceerd, bleek, dat 75%van een groep ondervraagde constructeurs van bekistingen voorverse betonspecie een s.g. van 2,4 aannam als basis voor de be-rekening. De vraag blijft, hoe de overige 25% de bekisting ont-wierp.De belangrijkste proeven, die van 1931 tot heden zijn genomen,geven zeer uiteenlopende cijfers voor de zijdelingse druk. Waar-schijnlijk is dit te wijten aan de allerminst uniforme opzet van deproeven.Deze proeven en hun resultaten zullen in dit artikel worden be-sproken, terwijl ook aandacht zal worden besteed aan de formules,die voor het betekenen van de druk op de bekisting van belangzijn.Uitgevoerde proevenIr. L. W. Teller (2)* bouwde in 1930 een houten kolombekistingmet een doorsnede van 0,20 0,90 m2en een hoogte van 3,60 m.In ??n wand van deze bekisting werden drukdozen aangebracht,die ongeveer uitgevoerd waren zoals de thans in Nederland ge-bruikte gronddrukdozen.Deze drukdozen bevonden zich op afstanden van 0,30 m, 1,05 m,1,80 m en 2,70 m van de voet van de bekisting. Op deze wijzewerden vijf kolommen onderzocht. Daar Teller de invloed van* Dit artikel, ?n het bijzonder de gedeelten betreffende de tri-axiale be-proeving van verse betonspecie, wordt gepubliceerd met toestemmingvan de Technische Hogeschool te Delft, Afd. Materi?le en TechnischeZaken, onderafdeling bouw- en onderhoudszaken.* De tussen haakjes geplaatste, cursieve cijfers verwijzen naar de littera-tuur-opgave aan het eind van dit artikel.het trillen wilde bestuderen, werd de betonspecie in twee kolom-men met de hand gepord en in de drie andere kolommen mecha-nisch verdicht. De verdichtingsapparatuur had een frequentie van3 600 omw./min.; zij werd aangebracht aan de buitenzijde van debekisting. De gebruikte betonspecies hadden verder nog ver-schillende zetmaten, vari?rend van 3,8 tot 10 cm. Overigens warende mengsels volkomen gelijk. De mengverhouding van cement:zand : grind was in volumedelen 1 :2 :4. Het zand en grind bezateneen vrij ronde korrelvorm. De snelheid waarmee de bekistingwerd gevuld, bedroeg 6 m/uur. Een schema van de opstellingvoor deze proef is weergegeven in figuur 1a.De meetresultaten bij verdichting met de kisttriller zijn in fig. 1bgeschetst.Onder invloed van het trillen bleek de verse betonspecie voor deberekening te kunnen worden beschouwd als een vloeistof meteen s.g. van 2,4. Een temperatuurverschil van ongeveer 3 ?C, dattijdens het onderzoek optrad, bleek op de druk weinig invloeduit te oefenen.Een soortgelijk onderzoek als hierboven beschreven, is gepubli-ceerd door de heren A. J. M. van Ey Ie en L Boersma in Cement11 (1959) Nr. 3 (3). Uit figuur 2 (blz.1058) blijkt, dat de druk onge-veer 3 en 4 uur na de aanvang van het storten een maximumbereikt.Prof. Dr.-lng. R. Hoffmann (4) liet een bekisting met een door-snede van 2,14 1,0 m2en een hoogte van 1,03 m vullen metbetonspecie. De twee korte zijwanden werden zodanig gestem-peld, dat elke beweging hiervan onmogelijk was. De beide langezijwanden daarentegen werden zodanig opgesteld, dat ze met zoweinig mogelijk wrijvingsverliezen in horizontale richting kondenbewegen. Deze wanden waren buiten de bekisting aan elkaar ge-koppeld door staven ?18, waarop rekmeters waren aangebracht.Om te voorkomen, dat de lange zijwanden ten gevolge van dedoor de verse betonspecie uitgeoefende druk zouden doorbuigen,waren zij verstijfd door middel van stalen damwandplanken.De betonspeciemassa bestond uit een kern met 180 kg cement perm3, waaromheen een 20 cm dikke schil met 250 kg cement per m3.De toeslagmaterialen bezaten een vrij ronde korrelvorm. Dewater-cementfactor voor de schil was 0,54 en voor de kern 0,70.De betonspecie werd in drie lagen aangebracht, de stijgsnelheidwas hierbij 0,35 m/uur. Elke laag werd met een Wacker-betontril-ler intensief getrild.Cement 12 (1960) Nr. 12 1057f/g. Ia. schematische opstelling van de proef van Tellerfig. 1b. de zijdelingse druk van verse getrilde betonspecie volgenswaarnemingen van Tellerfig. 2. gemeten druk van verse betonspecie op de bekisting van eenreservoir te Heemstede volgens Van Eyle en BoersmaNadat de bekisting geheel was gevuld, werd op de verse beton-specie een belasting geplaatst, in de vorm van stalen balken. Detemperatuur tijdens deze proef varieerde van 0-4 ?C. In figuur 3a-bis het principe van deze proef en het verloop van de druk op debekisting getekend.Bij Gemeentewerken Rotterdam wordt gemeten op eenzelfdewijze als Hoffmann dit deed. Door middel van rekstrookjeswordt de spanning in de centerpennen gemeten. In Cement 9(1957) Nr. 7-8 bij voorbeeld beschrijft ir. J. Aarnoudse dezemethode (Sa) (fig. 4 en 5).fig. . schematische opstelling van de proef van Hoffmannfig. 4. bekistingsdrukmetingen bij de reinwaterkelder te Rotterdamvolgens Aarnoudsestijgsneiheid = 0,85 m/uur = 12 ?CHarrison G. Roby, hoofdingenieur bij de Byllesby Engineeringand Management Corporation te Chicago onderzoent de druk aande voet van een kolom met een doorsnede van 0,758 X 0,758 m2eneen hoogte van 4,56 m. Hij maakte gebruik van een metalen plaat,waarvan de doorbuiging evenredig mag worden geacht aan dedruk, die er op wordt uitgeoefend. Hij varieerde de snelheid,waarmee de bekisting werd gevuld (3,00 m/uur en 0,30 m/uur),en verder het cementgehalte (1 : 3,5 -1 : 5,5 -1 : 7,5 in volume-delen); hij onderzocht de invloed van de temperatuur op de druk.Fig. 6 geeft de opstelling voor zijn proef en de resultaten. Debetonspecie werd bij deze proeven niet getrild.fig. 3b. de druk van verse betonspecie op de bekisting volgens1058 Cement 12 (1960) Nr. 12Tri-axiale beproeving van verse betonspecie (fig. 7)In opdracht van de Technische Hogeschool te Delft, Afd. Materi?leen Technische Zaken, onderafdeling bouw- en onderhoudszaken,is verse betonspecie in de tri-axiale pers beproefd.De betonspecie bevindt zich bij deze proef in een rubber manchet.Deze wordt, om vervorming tegen te gaan, omgeven door eenwatermantel. Bij een verticaal gerichte belasting op het beton-speciemonster, zal de betonspecie, voordat deze geheel vast is,via de rubber manchet een horizontale druk op de watermanteluitoefenen. Deze druk kan op een manometer worden afgelezen.De verticale belasting kan op elk gewenst tijdstip worden ver-hoogd; de hierbij behorende druk, die nodig is om het monstertegen vervorming te behoeden, zal steeds kleiner worden en tenslotte nul zijn, namelijk als de betonspecie vast is geworden.Uit deze proef is onmiddellijk af te leiden: de verhouding tussende verticale belasting (1) en de benodigde steundruk (2). Dezebetrekking is een maat voor de vloeibaarheid. In de grondmecha-nica wordt deze verhouding genoemd a, in formulevorm:Xa = |^ = tg2(4S-i9)Deze factor a speelt in vele formules een grote rol.fig. 7. tri-axiale beproevingspers fig. 5. bekist?ngsdrukmetingen bij de Leuvekeersluis te Rotterdamvolgens Aarnoudsestijgsnelheid = (l,34 - 2,82) m/uur = 12?CFactoren, die de zijdelingse druk in sterke mate be?n-vloedenUit de genoemde proeven bleek, dat de volgende grootheden indit verband belangrijk waren :1. de wijze van stortenIndien, zoals bij de proef van Teller, van een hoogte van 3,60 mwordt gestort, zal de onderste laag betonspecie lang vloeibaarblijven. De val van elk stort werkt dan als een soort stamper. Is devalhoogte gering, dan zal de betonspecie sneller opstijven.2. de wijze van verdichtenAls betonspecie wordt getrild, zal de hoek van inwendige wrijvingnul worden en zal de betonspecie zich als een vloeistof gedragen.Spoedig hierna blijkt de hoek van inwendige wrijving snel groterte worden. Wordt er niet getrild, dan zal er onmiddellijk na hetstorten een behoorlijk grote hoek van inwendige wrijving zijn.Deze zal echter maar langzaam toenemen in vergelijking met dievan getrilde betonspecie.3. de bindtijd van het cementDeze factor wordt in dit artikel aangegeven met ?. Is de bindtijdkort, dan zal de betonspecie snel stijf worden en daardoor zal dedruk op de bekisting niet hoog oplopen. Wanneer men uitgaat vaneen bepaalde maximum druk op de bekisting, dan zal het vullenvan de bekisting sneller kunnen geschieden naarmate de bindtijdkorter is. fig. ba. schematische opstelling van de proef van Robyfig. 6b. bekistingsdrukmetingen volgens RobyCement 12 (1960) Nr. 1210594. de snelheid v waarmee het niveau van de betonspecie in de bekistingstijgtWordt de gehele bekisting bij voorbeeld gevuld voordat het beginvan de binding intreedt, dan kan bij trillen van de betonspecie degehele massa als een vloeistof met een s.g. van 2,4 gaan werken.FormulesDe genoemde factoren heeft men getracht uit te drukken informules. Het begrip vloeibaarheid kan worden weergegeven methet symbool = tg2(45 - ?), waarin = hoek van inwendigewrijving. Deze term kan ook worden geschreven als:Is de betonspecie volledig vloeibaar, dan wordt, in overeenstem-ming met de wet van Archimedes, een op deze vloeistof aan-gebrachte druk in alle richtingen gelijkmatig voortgeplant, dusook in horizontale richting. In dit geval is dus a = 1. Als de beton-specie volledig is verhard, wordt de horizontale druk niet ver-hoogd bij het opvoeren van de verticale belasting. In dit gevalBijdezeformuleis voorde term 0. e 4? ?. ' de volgende op-merking te maken :Deze term moet nul zijn als de binding is be?indigd, want eenverticale belasting veroorzaakt in gebonden betonspecie geenhorizontaal gerichte druk.Dus als t = ? moet ? e 4. / =0 zijn. Dit is in deze for-mule niet het geval.Onderzoekingen van Stanley RodinIngenieur Stanley Rodin (figuur 9) onderzocht in 1952 alle tot opd?t ogenblik uitgevoerde proeven, ten einde tot een eenvoudigevuistregel te komen. Het bleef niet bij ??n regel: hij kwam name-lijk tot de volgende formules:3,--De volgens bovenstaande formules berekende druk geldt bij eenfig. 8. de vloeibaarheid van verse betonspecie bij -- 0,8 ?C volgensHoffmanntemperatuur van 20 ?C. Uit de grafiek in fig. tO is de factor af telezen, waarmee de druk bij 20 ?C moet worden vermenigvuldigdom de druk bij een andere temperatuur te krijgen.Onderzoekingen van Prof. A. GuerrinProf. A. Guerrin (6) onderscheidt voor de berekening viersoorten betonspecie:a. gietbetonspecie;b. zeer vloeibare vette betonspecie;c. aardvochtige betonspecie;d. trilbetonspecie.ad a. De druk wordt hier gescheiden gedacht in de drukvan het inde betonspecie aanwezige water en de druk van het cement-toe-slagmengsel.Hierdoor wordt de formule:P = v.t.Yv + X - y . t . Y t1060 Cement 12 (1960) Nr. 12waarin: v = stijgsnelheid van de betonspecie(in m/uur)t = tijd na het begin van het storten (in uren)v = s.g. water (in t/m3) = 0,413 voor houten bekisting en 0,445 voor metalenbekistingt = s.g. cement-toeslagmengsel = 1,2 (rekeninghoudend met de opwaartse druk)Dat de waarde van als constant wordt aangenomen, is niet inovereenstemming met de werkelijkheid, daar afneemt met detijd.ad b. In dit geval wordt aangenomen, dat de betonspecie zichgeheel als een vloeistof gedraagt. De druk wordt dan = Y. . t,waarin = s.g. verse betonspecie (in t/m3).ad . Voor het gehele mengsel wordt hier gerekend met = 0,30,zodat de druk wordt berekend volgens = 0,3 . . t.ad d. Bij trilbetonspecie wordt er rekening mee gehouden, datbetonspecie, die enigszins is opgestijfd, ten gevolge van het trillenweer geheel vloeibaar kan worden gemaakt tot een diepte van0,80 m. Voor deze laag kan = 1 worden aangehouden. Ligt hetbetonspecieniveau hoger dan 0,80 m boven het punt waar dezijdelingse druk moet worden berekend, dan houdt prof. G u e r r i nvoor de onder de vloeibare laag (van 0,80 m) gelegen betonmassarekening met een = 0,13.Voor de voet van de bekisting wordt de formule nu : = 0,8 ++ 0,13 ( . t - 0,8). Een bezwaar tegen deze formule is, dat == 0,13 niet als een constante voor de onderste laag mag wordenaangehouden. Onder bepaalde omstandigheden zal een waardehebben die aanzienlijk hoger dan 0,13 is.Onderzoekingen van R.Schj?dt (7)In het Noorse Geotechnisch Instituut is door R. Schj?dt dewaterspanning in de pori?n van verse betonspecie gemeten.Dit onderzoek resulteerde in een vrij ingewikkelde formule:>--[?(-4;)+?0-*4)]*waarin: Pmax = grootste druk die op de bekisting kan optreden = s.g. van de betonspecieh1 = de diepte waarop de trilling zich nog doet gevoe-lenh2 = stijgsnelheid bindtijdo = s.g. van water = de verhouding van de hoogte van de druk van hetwater in de pori?n tot de hoogte van het beton-specieniveau =tg2(45-?)In de grafische voorstelling van deze spanningen worden geentemperaturen vermeld. Voor getrilde betonspecie treedt na 2 totuur na het storten de grootste druk op.Verder wordt = 20? - 30? aangehouden, waardoor varieertvan 0,5-0,33. Bij geringe stijghoogte van de betonspecie, gepaardgaande met trillen, kan echter wel 1 zijn.Onderzoekingen van A.C.I. Commissie 622Deze commissie van het American Concrete Institute had tot taakom een eenvoudige, betrouwbare formule te ontwerpen voor deberekening van de druk van verse betonspecie. In Journal of theAmerican Concrete Institute, augustus 1958, wordt van deze onder-zoekingen een overzicht gegeven. In hoofdzaak werden met elkaarvergeleken de formules van Hoffmann en Rod in. Daar beide inonvoldoende mate bevredigden, is gezocht naar formules, die in depraktijk beter voldoen.Voor kolommen werd de formule:= 0'73+1- ({/ 2)Voorwanden, waarbij v< 3,50 m/uur:p = 0'73 +?lTr(t/m2)Cement 12 (1960) Nr. 12f/g. 10. invloed van de temperatuur op de zijdelingse betonspeciedrukvolgens Rod i Voor wanden waarbij > 3,50 m/uur: = 3,65 + ^j (t/m2)In al deze formules is vin m/uuren T?n?C.Onderzoekingen van NoackIn 1916 en 1917 verrichtte Noack in Berlijn bekistingsdrukproe-ven met betonspecie van verschillende consistentie. Hij promo-veerde in 1919 op het onderzoek naar de zijdelingse druk vanverse betonspecie en ontwikkelde in zijn dissertatie de formule:,.-1^(,..-1-0tgcp'-waarin: = zijdelingse druk (in t/m2)Y = s.g. verse betonspecie (in t/m3)' = wrijvingshoek tussen betonspecie en bekistingO = omtrek van de horizontale doorsnede over de be-kisting (in m)F = oppervlak van de horizontale doorsnede over debekisting (in m2)e = natuurlijke logaritme = 2,718= constante : voor aardvochtige betonspecie 0,401voor normale betonspecie 0,380voor gietbetonspecie 0,375= hoogte van het betonspecieniveau boven het meet-punt (in m)De temperatuur blijft hier geheel buiten beschouwing, terwijl aanOde vorm -- te veel betekenis wordt gehecht.Onderzoekingen van B?hmB?hm gebruikte (in 1928-1929) een soortgelijke formule voor on-eindig grote doorsnedenP = Y. v. t. twaarin: = zijdelingse druk (in t/m2)Y = s.g. verse betonspecie = stijgsnelheid (in m/uur)t = tijd (in uren) na het bereiken van het meetpuntt = tg2(45 - ? ), waarin = hoek van inwendigewrijving van verse betonspecie = 15?.Hij nam aan, dat in 12 uren rechtlijnig verloopt van 0,875 naar 0.Dit geldt echter slechts bij benadering als de betonspecie wordtverwerkt bij een temperatuur, die ?ets boven 0 ligt.1061fig. 11. de vloeibaarheid van verse betonspecie, bepaald met de tri-axiale beproevingspersWaarnemingen bij beproeving in de tri-axiale persBespreking van de waarnemingenIn flg. 11 zijn de resultaten van de tri-axiale beproeving van getril-de betonspecie weergegeven.Onmiddellijk na het trillen van de betonspecie in de cel moet = 1 zijn. De waarnemingen in de periode van 0-2 uur na hettrillen zijn hier aanmerkelijk lager dan verwacht mag worden. Bijhet overbrengen van de verticale belasting treden wrijvingsver-liezen op, waardoor slechts een deel van de verticale belastingeffectief is. Bij groter wordende verticale belasting worden dezeverliezen percentsgewijze minder.De proeven zijn uitgevoerd bij een temperatuur van 20 C. Hetbegin van de bindtijd is na 3? uur, het einde na ongeveer 6? uur.Duidelijk blijkt, dat de proef van Vicat, waarmee het begin en heteinde van de bindtijd bepaald worden, slechts aangeeft het be-reiken van een zekere sterkte. Het met deze proef aangegeventijdstip van einde bindtijd blijkt geenszins te betekenen, dat deverse betonspecie al volledig hard geworden is.Afleiding van de formuleVoor getrilde betonspecie zijn de waarnemingen weergegeven inde tabellen 1 en 2.De gezochte kromme zal die van een e-macht het meest benaderen.Deze macht moet een functie van de tijd t zijn. Als t = 0 moet demacht ook nul zijn opdat = 1. De algemene vorm van de verge-lijking voor t wordt dan:? = ?"?1of,daarXo = 1Xt = e-A?*Stel t = xeny = -A.tDan wordt het verschil tussen de waargenomen en de theoretischewaarden (y- A. ). Om de kleinste kwadratische verschillen metde theoretische lijn te krijgen, zal het differentiaalquoti?nt vanE(y-A.x)2gelijk aan nul moeten zijn.S(y-A.x)2= Sy2-2AE(x.y) + A2Ex2^^ = -2E(x.y) + 2ASx2= 0ASx2= S(x.y)A~ 2194A_34TA = 0,57De formule wordt nu t = e-0,571 voor betonspecie, die bij 20 ?Conderzocht wordt.Correlatie-berekeningOm na te gaan, in hoeverre de formule geldig is, kan een corre-latie-berekening worden opgezet. Hiertoe wordt de waarde vande correlatie-co?ffici?nt r berekend. Deze moet liggen tussen 0 en1 ; hoe dichter r tot 1 nadert hoe meer zekerheid bestaat, dat degevonden betrekking juist is.Uit de berekening voor de betrekking tussen en y zijn de volgen-de grootheden bekend (zie tabel 3): = 84,9 = 3,69 y = 48,452 y_ = 2,13 2=341 ? =14,80I y2=114,04 y2= 4,96!(.y)=194 x.y = 8,43De correlatie-co?ffici?nt is :(.) - _" m y ' i W M.-.yr = _ -iy>2-(x)2(>2-(D2(_______ 8,43-3,69 2,13j/(14,80 - 3,692) (4,96 - 2,132)r = 0,80Een waarde 0,80 voor r wordt beschouwd als bewijs voor eensterke correlatie.Vergelijking van de berekende en de in werkelijkheid ge-meten drukDe invloed van de temperatuurIn fig. 12 is met behulp van de gegevens van Harrison G. Robyaangegeven, hoe het verband is tussen temperatuur en de bindtijd.In fig. 13 (blz. 1064) blijkt, dat het begin van de bindtijd voor nor-maal Enci-cement overeenkomt met een vloeibaarheid () van0,17. Het einde van de bindtijd komt dan overeen met een vloei-baarheid () van 0,04.Beide gegevens zijn in deze figuur gecombineerd. Om de krommete bepalen, die de vloeibaarheid aangeeft, is uitgegaan van driebekende punten.a. Op de tijd 0: = 1;b. het begin van de bindtijd voor een bepaalde temperatuur (af-geleid uit fig. 12) wordt aangegeven op de lijn, die een vloei-baarheid van 0,17 voorstelt;het einde van de bindtijd (op dezelfde manier bepaald alsonder b) wordt vastgelegd op de lijn, die een vloeibaarheid van0,04 voorstelt.fig. 12. het verband tussen bindtijd en temperatuur volgens Roby1062 Cement 12 (1960) Nr. 12Tabel 1 Tabel 2zandgrindmengsel:zand < 0,15 mm 2,5%zand 0,15- 0,30 mm 5,0%zand 0,30-0,60 mm 7,5%zand 0,60- 1,40 mm 10 %zand 1,40- 2,80 mm 10 %grind 2,80- 5,60 mm 10 %grind 5,60-11,20 mm 20 %grind 11,20-23 mm 25 %grind 23 -30 mm 10 %Enci-cement: 750 gramwater-cementfactor: 0,5zand + grind : 5000 grambijzonderheden :mengsel getrild in de celtijdstip menging: 9.30 uurverticale belasting(in kg/cm2),tijdstip steundruk(in kg/cm2)2vloeibaarheid2^_1,27 9.45 u.10.00 u.0,480,450,380,351,59 10.00 u.10.15 u.0,530,530,250,251,91 10.17 u.10.30 u.0,620,620,280,282,23 10.30 u.10.45 u.0,710,710,280,282,54 10.45 u.11.00 u.0,780,780,220,222,86 11.00 u.11.15 u.0,830,830,160,163,18 11.15 u.11.30 u.0,900,900,220,223,50 11.30 u.11.50 u.1,021,020,370,373,82 11.50 u.12.05 u.1,081,070,190,164,14 12.05 u.12.20 u.1,141,140,220,224,45 12.20 u.12.35 u.1,191,200,190,224,77 12.35 u.12.50 u.1,241,250,130,165,09 12.50 u.13.05 u.1,301,300,160,165,43 13.05 u.13.35 u.1,351,360,160,135,73 13.35 u.14.00 u.1,401,400,130,136,05 14.00 u.14.15 u.1,411,410,040,046,37 14,15 u.14.35 u.1,421,450,060,136,69 14.35 u.14.50 u.1,461,480,030,097,01 14.50 u.15.05 u.1,501,500,060,067,33 15.05 u.15.20 u.1,521,520,090,137,65 15.20 u. 1,55 0,06samenstelling en bijzonderheden: zie tabel 1.tijdstip menging: 9.10 uur.verticale belasting(in kg/cm2),tijdstip steundruk(in kg/cm2)2vloeibaarheid21,27 9.25 u.9.45 u.0,680,530,540,421,59 9.45 u.10.05 u.0,630,590,310,191,91 10.06 u.10.25 u.0,670,650,250,192,23 10.25 u.10.45 u.0,760,750,340,312,54 10.45 u.11.05 u.0,830,820,250,222,86 11.05 u.11.25 u.0,880,880,190,193,18 11.25 u.11.45 u.0,950,950,220,223,50 11.45 u.12.05 u.1,051,050,310,313,82 12.05 u.12.25 u.1,111,110,190,194,14 12.25 u.12.45 u.1,191,190,250,254,45 12.45 u.13.05 u.1,221,220,090,094,77 13.05 u.13.30 u.1,271,270,160,165,09 13.30 u.13.50 u.1,321,320,160,165,43 13.50 u.14.10 u.1,351,350,090,095,73 14.10 u.14.30 u.1,381,380,090,096,05 14.30 u.14.50 u.1,401,400,060,066,37 14.50 u. 1,40 0,00Tabel 3Xx 2 2. N = 232,08 0,9942,33 1,6602,58 1,5142,83 2,0603,08 1,8323,33 1,8323,83 2,0404,25 3,220 2=341 (.) = 194 =84,9 /=48,452194 = -- = 0,57 y2= 114,04341 = 3,69, 7 = 2,13 ^=14,80 7 = 4,96= 8,434,50 2,8154,83 3,5005,08 2,8155,335,582,4052,8152,00 1,6602,33 1,1702,66 1,6603,00 1,3863,33 2,4053,66 1,8324,08 1,8324,41 2,4054,74 2,4055,08 2,815 = 84,9 = 3,69 = 48,4527 = 2,132= 3412= 14,802= 114,04y2= 4,96(.)=1943? =8,43Cement 12 (1960) Nr. 12 1063fig. 13.de vloeibaarheidvan verse beton-specie bijverschillendetemperaturenDoor genoemde drie punten wordt een vloeiende kromme ge-trokken. De kromme voor de bij 3 ?C komt in grote trekkenovereen met de kromme, die of f m a n n vond (zie flg. 8, blz. 1060).De vloeibaarheidskrommen voor 10?C en 20 ?C liggen niet ver uitelkaar. Daar de grootste druk op de bekisting ongeveer na verloopvan 2 uur optreedt, kan het verschil in vloeibaarheid op dit tijd-stip een maat zijn voor de correctie-factor, die voor de druk op debekisting in rekening moet worden gebracht. De vloeibaarheidna 2 uur is 0,47 bij 10 ?C en 0,36 - ij 20 ?C. De correctie-factor bij0,472 uur is dan---- X 100% = 130%. Deze waarde komt vrijwel0,36overeen met wat Rod i aangeeft (fig. 10, blz. 1061). Na 1 uur isdeze correctie-factor 110%, na 3 uur 160%; het gemiddelde vande drie tijden is 133%.OpmerkingOok de krommen, die genoemd worden op blz. 22 en 24 van hetCUR-rapport No. 7 (9), kloppen vrij goed met de temperatuur-correctiegrafiek van Rodin.Uit een berekening volgt, dat de krommen bij de verschillendetemperaturen kunnen worden voorgesteld door de volgendeformules:bijF=10?C: X = e-0,3t = e-0,03t.rT = 20?C: x = e-0,6t = e-0,03t.r=40? : X = e-1,5t = e-?,03t.T (bij benadering)De druk op de bekisting kan nu worden berekend met de formuleP = Y.y.t.e-0,03 T.tDeze druk is maximaal als de eerste afgeleide van deze vergelijkingnul is.-i? = . . -0- -'.(1-0,03 T.t) = 0Dus 1-0,03 T.t = 0t= 10,03d2P d2PDaar -- --- = - 0,03 7", d.w.z. --^ < 0, is de druk dus maximaal.at2dt21Na een tijd t = zal de druk op de bekisting haar grootstewaarde hebben bereikt. Deze grootste waarde is dan door sub-1stitutie van t = in de formule voor te vinden.Prof. Guerrin noemt als diepte, waarover de verse betonspeciedoor trillingen nog vloeibaar kan worden gemaakt 0,80 m. Ir. J.Aarnoudse stelt deze diepte op 1,00 m. Als we dit laatste aan-houden, moet voor t in rekening worden gebracht , = / ?]-,.V-y)Anders gezegd: in de grafiek = e-0,03 T.t schuift de vloeibaar-1 1heid bij t = - ,,. - naar de oorsprong over een tijdsinterval - uur,' 0,03 v,1 1dust=7Ten aanzien van grote, massieve betonconstructies kan wordenopgemerkt, dat hier voor een temperatuur van enkele gradenboven de buitentemperatuur mag worden ingevoerd. Dit vindtzijn oorzaak in de vrij grote hoeveelheid warmte, die in grotebetonspeciemassa's wordt ontwikkeld.Vergelijking van deze formule met door Harrison G. Roby (fig. 6,blz. 000 ) uitgevoerde proeven geeft het volgende resultaat.Voor de naar alle waarschijnlijkheid bij 38 ?C uitgevoerde proefvertoonde de betonspecie na 42 min. + 6 min. = 48 min. eenmaximale druk van 3900 kg/m2.Bij de proef werd de specie van bovenaf in de bekisting gestort,de valhoogte was dus voor de onderste lagen ruim vier meter.Verdere verdichting vond plaats door op de bekisting te kloppen.Hoewel het niet volkomen identiek is met het trillen door middelvan trilnaalden, leidt deze aanname tot vrij goed vergelijkbarecijfers.Waargenomen en berekende belastingsdrukkenIn tabel 4 zijn de met de formulesDit iseenvloeibaarheid, die overeenkomt met die van ongetrildebetonspecie. Betonspecie, die zich in de 'afloop' van een intensiefgetrilde betonspeciemassa bevindt en zo de bekisting vult, zalvoor een dergelijke waarde kunnen vertonen.Vanwege deze grote afwijking met normaal geachte omstandig-heden voor getrilde betonspecie zijn de waarnemingen voor deNieuwe Leuvekeersluis bij de verdere berekening buiten be-schouwing gelaten.Uit de berekening blijkt:de gemiddelde afwijking is = -- = 3%, d.w.z. de berekendedruk was gemiddeld 103% van de gemeten druk. Uit veiligheids-overwegingen is dit een vrij gunstig gemiddelde.De standaardafwijking bedroeg_ /(!-)2. .--V --M_I-- waarin: x; = waargenomen verschil, ------ = gemiddeld verschill/212S , ,= I/ N = aantal waarnemingen= 11,51064 Cement 12 (1960) Nr. 12Tabel 4Proef: gemeten(in kg/m2)berekend(in kg/m2)afwijking(in %)Teller: cel no. 1 8 044 8 044 0(.2) 4 720 6 355 + 35cel no. 2 6150 6 200 + 14125 4 910 + 19cel no. 3 4150 4 320 + 43 075 3 413 + 11cel no. 4 2 050 2160 + 51 617 1728 + 7Hoffmann: niet te vergelijken volgens zijn opmerking dien-(4) aangaandeAarnoudse:(5a) reinwaterkelder 2 700 2 734 + 12 500 2 020 - 19Aarnoudse:(Sb) nieuweLeuvekeersluiscenterpen no.4 2 200 3 500 + 59centerpen no. 3 2 800 4 300 + 54centerpen no. 2 3 400 3 066 - 10centerpen no.1 600 1 344 + 124Van Eyle en Boersma: 2160 2 246 + 4(3) 1 900 1653 - 13800 911 + 14Roby: = 3 m/uur 3 900 3 425 - 11 = 1,20 m/uur 3 400 3 235 - 5 = 0,60 m/uur 2 800 2 497 - 11 = 0,30 m/uur 2100 2 420 + 15De standaardafwijking is hier groot ten opzichte van het gemid-delde verschil. Hierin komt tot uiting, dat bij het meten van dedruk op de bekisting nog allerlei factoren een rol spelen, die nietin de gebruikte formule tot uiting komen.De vraag, of de formule dan nog wel bruikbaar is, is opgelost doorde verdeling van de waargenomen verschillen te onderzoeken.Uit dit onderzoek bleek, dat voor deze verdeling mag wordenaangenomen, dat de verschillen volgens een zogenaamde Gausz-kromme zijn gerangschikt. Hierbij werd de X2-test toegepast.De waarschijnlijkheidsrekening leert, dat bij rangschikking van dewaarnemingen volgens een Gausz-kromme het volgende geldt:spreiding van de uitkomsten:x? s in 68,2% van de waarnemingen ? 2s in 95 %....................... , ? 3s in 99,7% ,, ,,Uit bovengenoemde cijfers is de betrouwbaarheid van de ge-bruikte formule af te leiden, namelijk:91,5%-114,5% v. d. berekende druk in 68,2% v. d. waarnemingen80 %-126 % ,, ,, ,, ,, ,, 95 % ....................68,5%-137,5% ,, , ...............................99,7% , ..................ConclusiesWijze van verdichten. Deze is voor de zijdelingse druk van versebetonspecie van groot belang. Ongetrilde betonspecie zal onmid-dellijk na het storten, mits dit van geringe hoogte gebeurt, eenvloeibaarheid van ten hoogste 0,5 vertonen.Bij toepassing van trillers op de bekisting blijft de betonspecievrijwel geheel vloeibaar over het oppervlak waar trillingen nogwaarneembaar zijn.Bij normaal trillen van de betonspecie verloopt de druk volgensde formule:Temperatuur. De invloed van de temperatuur van de buitenluchtwordt uitgedrukt in het symbool T. Bij betonconstructies, waar-van de kleinste afmeting 2,50 m is, zal de bij de verharding vrij-komende warmte met ongeveer 2 ?C verhogen.Cementsoort. De in fig. 13 geschetste krommen gelden voor port-landcement. Volgens gegevens uit CUR-rapport No. 7 (9) is hetverschil tussen de cementklassen , en hier van weinig bete-kenis.Voor hoogovencement zullen de krommen iets vlakker lopen.Uitgaande van het begin van de binding van hoogovencement na4 uur, en het einde van de binding na 9 uur (bij een temperatuurvan 20 ?C) kan de kromme als volgt worden berekend : = 0,17 = e-A.4 =e-1,8 A = 0,45 = 0,04 = e-A.9 =e-3,3 A = 0,37Bij 40 ?C wordt het: = 0,17 = e-A.5/s = e-1,8 A = 1,08 = 0,04 = e-A.'% = e-3,3 A = 1,00Door de berekening ook voor 60 ?C op te zetten wordt gevonden,dat voor hoogovencement de formule voor wordt = e-OfllST.tVoor andere cementsoorten kan de kromme op soortgelijke wijzeworden bepaald.Cementhoeveelheid. Als per m3beton 250?400 kg cement wordtverwerkt, gelden de in het voorgaande afgeleide formules. Bovende 400 kg cement per m3zal de ontwikkelde bindingswarmte deverharding versnellen en een gunstige invloed hebben, zodatlagere maximumdrukken zullen worden bereikt.De water-cementfactor heeft bij getrilde betonspecie weinig ofgeen invloed.Bekisting. De wrijving van de betonspecie tegen de wand heeft bijdeze formules weinig of geen betekenis. Het silo-effect verandertmet de vloeibaarheid van de betonspecie en gaat waarschijnlijkpas een merkbare invloed uitoefenen nadat de maximale druk isopgetreden.Een dicht wapeningsnet kan wel van betekenis zijn.Injectiebeton. Bij injectiebeton wordt de druk op de bekisting be-paald door de volgende drie factoren:o. dedrukvan de toeslagmaterialen: P, = H.(1-p).Yt.tg2(45-^)b. de druk van de mortel, verlopend volgens :P2=Ym.v.t.e-.0,?3T.tc. de opdrijvende kracht van de mortel:P3 = -(1-p)-V -t -(Yt -Ym )hierin is = hoogte grove toeslagmaterialen in de bekisting = holle ruimte in de grove toeslagmaterialenYt = s.g. grove toeslagmaterialen = hoek van inwendige wrijving van de grove toeslag-materialenYm = s.g. injectiemortel = stijgsnelheid van de mortel (in m/uur)t = tijd na het begin van de injectie (in uren) = temperatuur van de omgeving (in ?C).Litteratuur1. Ellsberg, Harry - 'Pressures on formwork', Journal of theAmerican Concrete Institute, augustus 1958, blz. 173/190.2. Teller, L. W. - 'The effect of vibration on the pressure ofconcrete against formwork', Public Roods, Volume 12, no. 1,1931, biz. 11/16.3. Eyle, A.J. M. van en Boersma, L. - 'Gemeten betonspecie-druk op een wandbekisting', Cement 11 (1959) Nr. 3, biz.262/266.4. Hoffmann, R. - 'Der Schalungsdruck von frischem Beton',Beton- und Stahlbetonbau, 42e jaargang, Heft 17-18,15 septem-ber 1943, blz. 130/135.5a. Aarnoudse, J. - 'De bouw van een reinwaterkelder van25 000 m3inhoud te Rotterdam', Cement 9 (1957) Nr. 7-8,blz. 306/307.5b. Aarnoudse.J.-'De werken aan de Maasboulevard. II. Water-bouwkundige werken. Bekistingdrukmetingen', De IngenieurNr. 40, 2 oktober 1959, blz. 174/175.6. Guerrin, A.-'Druk van vers beton op de bekisting', Cement3(1951) Nr. 7-8, blz. 127/133.7. Schj?dt, R. - 'Schalungsdruck des Betons" und Porenwasser-druck', Beton- und Stahlbetonbau, 51 e jaargang, Heft 11, novem-ber 1956, blz. 241/244.8. Durand, P. - 'La d?termination des coffrages m?talliques',L'Equipement m?canique des mines, carri?res et grandes entre-prises, no. 228, oktober 1948.9. C.U.R.-rapport No. 7' - Versnelde verharding van beton doorverwarming', blz. 21/28.10. Graf, . en Kaufmann, F. - 'Schalungsdruck beim Betonie-ren', Deutscher Ausschuss f?r Stahlbeton, Heft 135.Cement 12 (1960) Nr. 12 1065