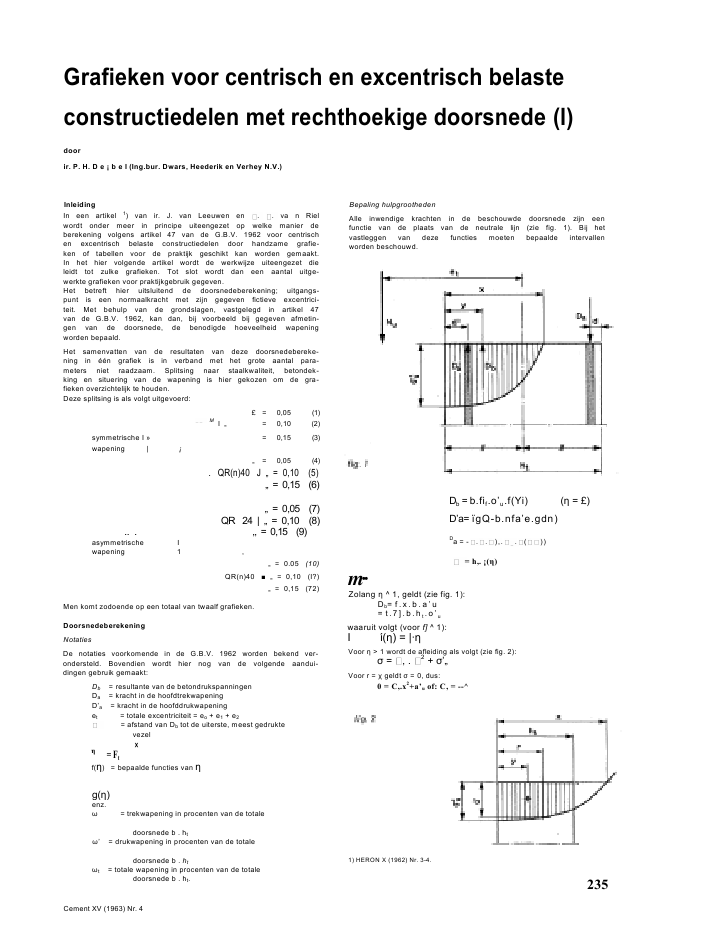
Grafieken voor centrisch en excentrisch belasteconstructiedelen met rechthoekige doorsnede (l)doorir. P. H. D e ? b e I (Ing.bur. Dwars, Heederik en Verhey N.V.)InleidingIn een artikel 1) van ir. J. van Leeuwen en . . va n Rielwordt onder meer in principe uiteengezet op welke manier deberekening volgens artikel 47 van de G.B.V. 1962 voor centrischen excentrisch belaste constructiedelen door handzame grafie-ken of tabellen voor de praktijk geschikt kan worden gemaakt.In het hier volgende artikel wordt de werkwijze uiteengezet dieleidt tot zulke grafieken. Tot slot wordt dan een aantal uitge-werkte grafieken voor praktijkgebruik gegeven.Het betreft hier uitsluitend de doorsnedeberekening; uitgangs-punt is een normaalkracht met zijn gegeven fictieve excentrici-teit. Met behulp van de grondslagen, vastgelegd in artikel 47van de G.B.V. 1962, kan dan, bij voorbeeld bij gegeven afmetin-gen van de doorsnede, de benodigde hoeveelheid wapeningworden bepaald.Het samenvatten van de resultaten van deze doorsnedebereke-ning in ??n grafiek is in verband met het grote aantal para-meters niet raadzaam. Splitsing naar staalkwaliteit, betondek-king en situering van de wapening is hier gekozen om de gra-fieken overzichtelijk te houden.Deze splitsing is als volgt uitgevoerd:? = 0,05 (1)MI ,, = 0,10 (2)symmetrische I ? = 0,15 (3)wapening | ?,, = 0,05 (4). QR(n)40 J ,, = 0,10 (5),, = 0,15 (6),, = 0,05 (7)QR 24 | ,, = 0,10 (8).. . ,, = 0,15 (9)asymmetrische Iwapening 1 ,,, = 0.05 (10)QR(n)40 ,, = 0,10 (I?),, = 0,15 (72)Men komt zodoende op een totaal van twaalf grafieken.DoorsnedeberekeningNotatiesDe notaties voorkomende in de G.B.V. 1962 worden bekend ver-ondersteld. Bovendien wordt hier nog van de volgende aandui-dingen gebruik gemaakt:Db = resultante van de betondrukspanningenDa = kracht in de hoofdtrekwapeningD'a = kracht in de hoofddrukwapeninget = totale excentriciteit = eo + e1 + e2= afstand van Db tot de uiterste, meest gedruktevezel= Ftf() = bepaalde functies van g()enz. = trekwapening in procenten van de totaledoorsnede b . ht' = drukwapening in procenten van de totaledoorsnede b . htt = totale wapening in procenten van de totaledoorsnede b . ht.Cement XV (1963) Nr. 4Bepaling hulpgroothedenAlle inwendige krachten in de beschouwde doorsnede zijn eenfunctie van de plaats van de neutrale lijn (zie fig. 1). Bij hetvastleggen van deze functies moeten bepaalde intervallenworden beschouwd.Db = b.fif.o'u.f(Yi) ( = ?)D'a= ?gQ-b.nfa'e.gdn)Da = - . . ),. . ( ))= h,. ?()m??Zolang ^ 1, geldt (zie fig. 1):Db= f . x. b. a 'u= t.7].b.ht .o'uwaaruit volgt (voor f] ^ 1): () = |?Voor > 1 wordt de afleiding als volgt (zie fig. 2): = , .2+ ',,Voor r = geldt = 0, dus:0 = C,.x2+a'u of: C, = --^1) HERON X (1962) Nr. 3-4.235De formule voor de spanningskromme wordt dan : = -?.,*+',,en de oppervlakte van het gearceerde deel :htF=y*{-^.r*+a'u}.drht ht= -^yV.dr+a'^dr= -^.i.ht3+0-'u.n,= ht.o'un-*.^?}= ht.c',,{l-H^)2}Tezamen met het gestelde bij fig. 1 geldt dus voor > 1 :9():Zodra de neutrale lijn in de buurt van de plaats van de druk-wapening valt zal de spanning in deze wapening niet meergelijk aan de vloei- of stuikspanning van het staal zijn. De ver-lenging of verkorting is dan te klein en een spanning evenredigmet deze verlenging of verkorting treedt op.De grenzen van dit gebied worden als volgt bepaald (zie fig. 3): 3,5 . IQ'3d'~3,5.10-3-- e'ax_ 3,5.10-3a^ht~ 3,5."3-- e'a "hiEr is sprake van een grensgeval indien:' = '. of:' '. ."?- = -?-? dUS:' = ?Wanneer deze waarde wordt ingevuld, dan vindt men: _ 3,5. IQ'3d'hf^3,5.10-3-^^Wanneer -- = YJbiovengrens) en E = 2,1. 10?kg/cm2worden in-"tgevuld, dan verkrijgt men:1 &^ 1 --0,136 O'e.10-3'htOp identieke wijze vindt men:_ 1 _____ d'TQolndergrens) ~ + 0,136 CTe . 10"3' ht236Het gebied is nu afgebakend, het verloop van g{r?) binnen ditgebied wordt als volgt gevonden:' = e'a. EUit fig. 3 volgt: x-d'x -- d' = -------------- .3,5.103. Ee'a =^-. 3,5.10-3*> =(l ---------- ).3,5.10-3. 2,1.10s= (1--).7,35.103Door invoering van f} verkrijgt men:d;' = {1-^).7,35.103Waaruit dan, tezamen met het gestelde bij figuur 1 (blz. 235),volgt:I *.>-?-0-flVoor Y] < Tf]0 geldt steeds: 9(77) = -1voor 7)>7] vindt men:1 g(4) = +1waarbij dan stilzwijgend verondersteld is: a'e=ae (overeen-komstig art. 47 van de G.B.V. 1962).):De berekening verloopt op analoge wijze als voor g(r?). Vol-staan zal worden met de uitkomsten:? =1+0,136 -11-^1^= -0,136 . (1-^Voor 1 wordt de afleiding met behulp van figuur 2(blz. 235):statisch moment t.o.v. meest gedrukte vezely =------------------------------------------------ --------------------oppervlakte gearceerde deelht=f{-Q.i*+o'u}.r.dro________________________F, ht h,-^r/V.dr+o'u ir. dr= o_____________ ei ______FCement XV (1963) Nr. 4-?1-i-V+aVi-h?2_F?.ht?.0'u.{2-(lp}hfO'g.{l-?.(i)2}2-(-)2= f.ht._a_Tezamen met het gestelde bij fig. I (biz. 235) volgt hieruit:2_(lp?() = ? ---- y3-(/Van groter belang blijkt het produkt van f(Yj) en ?() te zijn,daarvoor geldt:voor ^ 1 :?).!(! = ?- ? = 1?2voor > 1 :2_(lpm ?() = {1-J - 2} - i ------? = i {2-2} =3-(1)2 = t-j.(l)*Ter illustratie zijn in tabel I de intervallen en functiewaardenvoor QR 24 ( = 2400 kg/cm2) en -?- = 0,05 bijeengebracht."t(Hierbij is ook weer a'e = ae gesteld en bovendien d' = d).Tabel 1functie interval functiewaarde() 0 < < 1 > 1i-9() 0 < < 0,0380,038 < < 0,074 > 0,0743,071? 1,41+ 12 913,06+ '-- 1f(v?). ?() 0 < < 1 > 1i 2Afleiding bij s y m m e t r i s c h e wapeningBeschouwd wordt de betreffende doorsnede zoals aangegevenin fig. I (biz. 235).De evenwichtsvergelijkingen V = 0 en M = 0 leveren ons devergelijkingen waarmee de grafieken kunnen worden samen-gesteld.2V = 0: N,,-D'a-Db + Da = 0of: Nu = Db + D'a-DaDoor invoering van functies van verkrijgt men:'Nu = . h,. ',, . {) + . . h,. a',.. () --~ . . . . )Cement XV (1963) Nr. 3Stelt men nu ' = ' = \ . ?)t en deelt men door b. ht. ',, dankrijgt men:4 = 0 (momentenevenwicht om het hart van dedoorsnede) :- Ng. e, + Db . (J . h, - y) + D'a . (J . h, - d') ++ Da.(t.h,-?D = 0trf r _Db (i /it-y) + D'a (? ht-o") + D, . (j . ht --d)' * N,,Na invoering van functies van :b.h,.o'u .f(4 ).{J.hf -ht .i(4 )}+ ^l.b./it Xet= --------------- _ ----------------------------------------------- . ---------_X a'e. (). (i. h, - d') +^. . h,. . ). (J. h, - d)Vereenvoudiging is mogelijk door te stellen (? = t 2400 ... ....aV^=f(r])+2?0-l35--^!-hW>= f(?))+ 0,0889. ,.{()-- )}Uit vergelijking (2) volgt:i Hfl) - () ? ?() + 2? ? ^. 0,45 {g(Y]) + )}Nua'u.b.hf4 (! - f(7j). ) + 0,0400. ,. {9() + )}Nua'u.b.hfVoor het interval 0,027 < < 0,038 wordt dit:;- = 1-4 + 0,0889. ,. (-1 -i) =a ,,. b.hf= ?. -- 0,178. ,et_ ?--J2+ 0,0400.,. (-1 + 1) ?.-,h, Nu Nua'u.b.hf a'u-b.hf237Voor het interval 0,038 < < 0,074:-, ^ = f + 0,0889. ,. (3,06 --?'~ --1) == |. + ,. (0,183-?,J. -- J.2+ 0,0400.,. (3,06-^ + 1)et_____________________________________]T _______a'u.b.hfj.,., + ,.(0,162-^)a'g.b. h,Voor het interval 0,074 < < 0,716:_7-?^ = f.+ 0,0889. , (+1-1)=|.et _ i -- i 2+ 0,0400 . J0 959= ?. + ,. (0,361 -^-)i. -- ? . 2+ 0,0400 . ,. (+1 +----3,06)_= Nu='? b./it|.-?2+ ,.(^-0,082)= Nua'u.b.htVoor het interval 1,00 < < 1,41 .? 1 0 259 u. b. ?7t , * - i ? 2- * + * ( ^)2+? ? (--- ? 1,41 :- , Nh . = ! -* 2+ 0-0889. ,. (+ 1 + 1) == 1-|?2+ 0,178.,^.(-)2+ 0,0400. ,. (+1 -- 1)?t _______ 7j_____________________________a'u.b.ht_L (1)2N,,a'u.b.ht238In de grafieken is horizontaal -?- en verticaal ----?--?- (=T-S Xht a . b. nt 1,8NX ----r--r-) uitgezet. Ter wille van het gemak is dus reeds doora u-b.htde veiligheidsfactor 1,8 gedeeld. Men kan zodoende van deoptredende normaalkracht uitgaan. De gang van zaken bij hetvervaardigen van de grafiek is, dat in een bepaald interval eenzekere waarde van wordt gekozen en dat dan met een even-eens aangenomen waarde van t de plaats van deze combina-tie in de grafiek wordt berekend met behulp van het bij ditinterval behorende tweetal formules. Nadat een voldoendeaantal punten is bepaald kunnen lijnen worden getrokken voorgelijke t en voor gelijke .Het gebruik van de grafieken is zeer eenvoudig. Het meestvoorkomend zal zijn, dat men bij gegeven N en et de afmetingenvan de doorsnede schat en zo de waarden van de dimensielozeN e,parameters ----?--?- en j- bepaalt.a . . ntDe plaats in de grafiek van het punt dat door deze waardenwordt bepaald geeft dan aan, hoe groot het wapeningspercen-tage minimaal zal moeten zijn. Ook een omgekeerde werkwijzeis uiteraard mogelijk.Om vrij nauwkeurige aflezing van het wapeningspercentagemogelijk te maken is ?-- op logaritmische schaal uitgezet. Aan-htgezien dit nog niet voldoende was om de lijnen voor