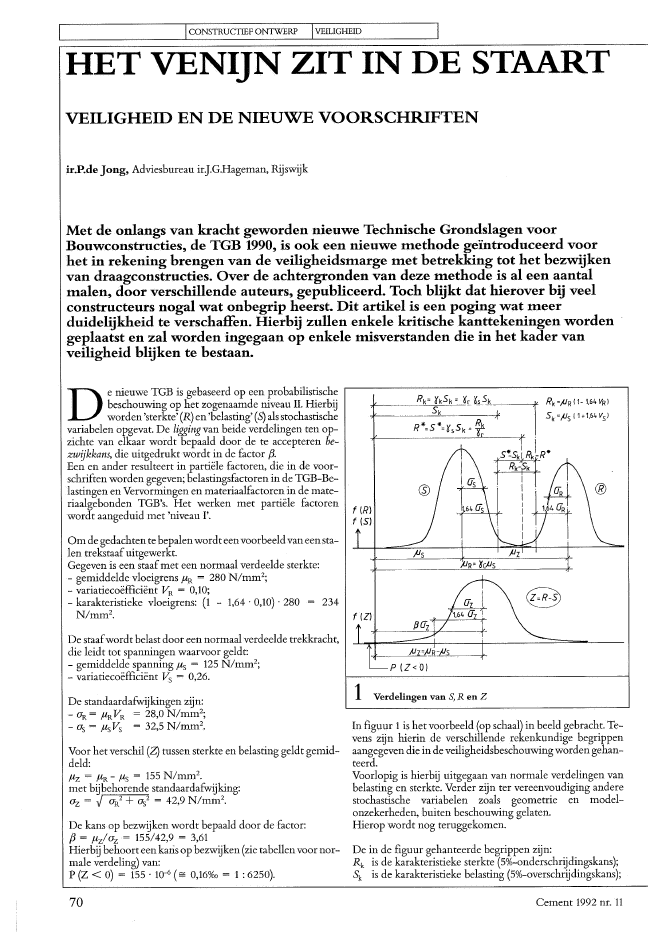
I ICONSTRUCTIEFONTWERP IVEILIGHEID IHET VENIJN ZIT IN DE STAARTVEILIGHEID EN DE NIEUWE VOORSCHRIFTENir.P.de Jong, Adviesbureau irJG.Hageman, RijswijkMet de onlangs van kracht geworden nieuwe Technische Grondslagen voorBouwconstructies, de TGB 1990, is ook een nieuwe methode ge?ntroduceerd voorhet in rekening brengen van de veiligheidsmarge met betrekking tot het bezwijkenvan draagconstructies. Over de achtergronden van deze methode is al een aantalmalen, door verschillende auteurs, gepubliceerd. Toch blijkt dat hierover bij veelconstructeurs nogal wat onbegrip heerst. Dit artikel is een poging wat meerduidelijkheid te verschaffen. Hierbij zullen enkele kritische kanttekeningen wordengeplaatst en zal worden ingegaan op enkele misverstanden die in het kader vanveiligheid blijken te bestaan.De nieuwe TGB is gebaseerd op een probabilistischebeschouwing op het zogenaamde niveau 11. Hierbij? worden 'sterkte' (R) en 'belasting' (Sj alsstochastischevariabelen opgevat. De ligging van beide verdelingen ten op-zichte van elkaar wordt bepaald door de te accepteren be-zwijkkans, die uitgedrukt wordt in de factor {3.Een en ander resulteert in parti?le factoren, die in de voor-schriften worden gegeven; belastingsfactoren in de TGB-Be-lastingen en Vervormingen en materiaalfactorenin de mate-riaalgebonden TGB's. Het werken met parti?le factorenwordt aangeduid met 'niveau I'.Omde gedachten te bepalenwordt eenvoorbeeld vaneensta-len trekstaaf uitgewerkt.Gegeven is een staafmet een normaal verdeelde sterkte:- gemiddelde vloeigrens flR = 280 N/mm2;- variatieco?ffi??nt VR = 0,10;- karakteristieke vloeigrens: (1 - 1,64?0,10)?280 234N/mm2?De staafwordt belast door een normaal verdeelde trekkracht,die leidt tot spanningen waarvoor geldt:- gemiddelde spanning fls = 125 N/mm2;- variatieco?ffici?nt Vs = 0,26.De standaardafWijkingen zijn:- ?OR = flR VR = 28,0 N/mm2;- Gs = fls Vs = 32,5 N/mm2?Voor het verschil (Z) tussen sterkte en belasting geldt gemid-deld:flz = flR - fls = 155 N/mm2?met bijbehorende standaardafWijking:Gz = J Gg2+ GS2= 42,9 N/mm2?De kans op bezwijken wordt bepaald door de factor:{3 = flzlGz = 155/42,9 = 3,61Hierbij behoort een karis op bezwijken (zie tabellenvoor nor-male verdeling) van:P (Z < 0) = 155 . 10-6 (== 0,16%0 = 1 : 6250).70f (R)f (S)1 Verdelingen van S, R en ZIn figuur 1is het voorbeeld (op schaal) in beeld gebracht. Te-vens zijn hierin de verschillende rekenkundige begrippenaangegeven die in de veiligheidsbeschouwing worden gehan-teerd.Voorlopig is hierbij uitgegaan van normale verdelingen vanbelasting en sterkte. Verder zijn ter vereenvoudiging anderestochastische variabelen zoals geometrie en model-onzekerheden, buiten beschouwing gelaten.Hierop wordt nog teruggekomen.De in de figuur gehanteerde begrippen zijn:Rk is de karakteristieke sterkte (5%-onderschrijdingskans);Sk is de karakteristieke belasting (5%-overschrijdingskans);Cement 1992 nr. 11Indien de karakteristiek? waarde door een andere dan de 5%-grens wordt gedefinieerd, dient voor 1,64 een ander getal teworden ingevuld.YR'YSYef3is de rekenwaarde van de sterkte, respectievelijk belas-ting;is de materiaal-, respectievelijk belastingsfactor;is de centrale veiligheidsco?ffici?nt, dit is de veilig-heidsco?ffici?nt tenopzichtevangemiddeldewaarden;is de veiligheidsco?ffici?nt ten opzichte van karakte-ristieke waarden;is de fractielfactor.1- 1,64 VRYk = 1 + 1,64 VsYe(6)De fractielfactor bepaalt de kans op bezwijken (bij bijvoor-beeld f3 = 1,64 hoort een bezwijkkans van 5%, bij f3 = 3,61 van0,16%0).Methoden ter bepaling van de veiligheidstnargeOnderlinge l?ggingIn het voorbeeld is de factor f3 met bijbehorende bezwijkkansberekend bij gegeven verdelingen van R en S.Een dergelijke berekening is als controleberekening te be-schouwen. Bij een ontwerpberekening zal de ligging van R enS moeten worden bepaald bij gegeven f3, uitgaande van een teaccepteren bezwijkkans. De liggingvanbeide verdelingen tenopzichte van elkaar kan daarbij worden gedefinieerd door:- een marge tussen degemiddelde waarden JlR en Jls, aangeduidmet centrale veiligheidsco?ffici?nt Ye;- een marge tussen de karakteristieke waarden van R en S, be-trokken op de 5% onder-, respectievelijk overschrijdings-kans, aangeduid met Yk;- parti?lefactoren, waarbij de marge tussen ~ en Sk wordt op-gedeeld in twee factoren YR en Ys (YRYs = Yk)'Centrale veiligheidscoiiffici?nt (yJDe centrale veiligheidsco?ffici?nt Ye is betrokken op de ge-middelde waarden van R en S.Er geldt dan (fig. 1}Het linkerlid wordt nu de rekenwaarde van de 'sterkte'(R*) ge-noemd en het rechterlid de rekenwaarde van de 'belasting' (S*).De berekening kan dan worden weergegeven in de gelijkheidR* = S* (zie ook fig. 1), ofbeter gezegd:voldaan moetwordenaan de voorwaarde: R* ;;::: S*.(7)JlR - JlsParti?le veiligheidifactorenVoorheen waren de Nederlandse voorschriften gebaseerd opde veiligheid ten opzichte van de karakteristieke waarden Yk'In verband met aansluiting aan internationale voorschriften,met name de Eurocodes, werd het gewenst geacht deze Yk opte splitsen in twee factoren, te weten de materiaalfactorYR (c.q.Ym) en de belastingifactor Ys (c.q. Yr)'De bepaling van beide factoren berust op onderstaande aflei-ding:= Jlzai= 2 Jlzazak + a~Jlzaiak a~JlR 2 Jlz = Jls +2 Jlzaz az(1)JlRYe = -JlsVeiligheid ten opzichte van karakteristieke waarden (yJMet formule (5) is het probleem volledig bepaald. Het is ech-ter niet gebruikelijk om de veiligheid te betrekken op de ge-middelde waarden, maar op de karakteristieke waarden (5%-grens) van R en S. Deze marge kan door middel van een 'ver~houdingsgetal' uit Ye worden afgeleid (zie ook fig.1):Deze noodzakelijke marge tussen JlR en Jls kan bij gegeven f3worden bepaald als nog twee kengetallen van de verdelingenbekend zijn. Dit zijn de variatieco?ffici?nten van R en S:aR asVR = - en lIS = - (2)JlR JlsHet verband tussen de vier grootheden f3, Ye' VR en Vskan alsvolgt worden bepaald:f3 = Jlz = JlR - Jls (3)az J ar., + a~Substitutie van (1) en (2) geeft:Ye- 1f3 = J y2V 2+ v.2eRSHieruit kan Ye worden bepaald:_ 1 + f3J Vr., + V~ ~ f32V~Vr.,Ye - 1 - f32Vr.,(4)(5)Uit enige omrekening volgt dat de parti?le factoren als volgtkunnen worden uitgedrukt als een functie van de variatie-co?ffici?nten FR en Vsen de centraleveiligheidsco?ffici?nt re:YR = (1 1,64 VR) V! + y~ V: (8)VS+YeVRYs = Ye V~ + y~Vr., (9)1 + 1,64 V s V~ + y~ VkHet produkt komt overeen met formule (6) (Yk = YRYS)'Nadere beschouwingDe drie hiervoor gegeven methoden bevatten dezelfde infor-matie en zijn dan ook volkomen gelijkwaardig.De in de nieuwe voorschriften gegeven methode - metparti?-le factoren - is onder meer gekozen om op eenvoudige wijzede verschillen in belastingstypen tot uitdrukking te kunnenbrengen. Noodzakelijk is dit echter niet, omdat dit zelfde ef~fect ook in de beide andere benaderingen (via Ye of Yk) kanworden bereikt.Het gebruik maken van parti?le veiligheidsfactoren moet dusniet worden gezien als een essenti?le wijziging in de veilig-heidsfilosofie, maat slechts als een alternatieve, praktisch han-teerbare presentatie.Uit de afleiding van formule (7) volgt verder dat de definitievan de rekenwaarden is gebaseerd op een min ofmeer arbi~traire keuze (zie ookfig. 1).Deze keuze is in die zin logisch, datCement 1992 nr. 11 71ICONSTRUCTIEFONTWERP IVEILIGHEID0,4VR = 0,200,30,20,1=0,15"j-----+--.-.,.~--t---:-= 0,101,21,42,01,82,4-.---'1,62,2~ 1,01Dit houdt tevens in dat het niet mogelijk is materiaal~onafhankelijke belastingsfactoren en belasting-onafhankelijkemateriaalfactoren te bepalen, die voldoen aan de wiskundigeuitgangspunten.Hier wordt met nadruk op gewezen omdat dit een bron vanmisverstanden blijkt te zijn. Deze misverstanden ontstaan metname doorhetfeit datdebelastingsfactorenindeTGB-Belas-tingen en de materiaalfactoren in de materiaal-gebondenTGB's zijn gegeven. De in het hoofdstuk materiaaleigen~schappen van de VEC gegeven materiaalfactoren mogen be- I------~~~~~---------.-.,.---____islist niet als een materiaaleigenschap worden gezien! 2 Verband Yk- Va.- Vs(normale verdeling)de rekenwaarde van de sterkte in grote mate wordt bepaalddoor het aandeel van de sterkte in de totale spreiding (uitge-drukt in de verhouding ~Ioz) en de rekenwaarde van de be-lasting door het aandeelvan de belasting in de totale spreiding(via de verhouding os!oz). Omdat in beide rekenwaarden Ozvoorkomt, wordt de belastingsfactor echter mede bepaalddoor de materiaalspreiding en de materiaalfactor mede doorde spreiding in de belasting. Deze 'kruiselingse' be?nvloedingkan betrekkelijk groot zijn.Veiligheid alsfunctie van spreidingIn figuur 2 is Yk uitgezet als functie van de variatieco?f-fici?nten VR en Vs(bij f3 = 3,6).Indezefiguuriseenopmerke-lijke tendens te zien, die een nadere verklaring vereist.Bij VR = 0,10 neemt Yk toe met Vs,terwijl ditbij VR = 0,20 an-dersom is. VR = 0,15 neemt een tussenpositie in; hier is Ykvrij-wel onafhankelijk van Vs.Dat bij VR = 0,20 de 'veiligheidsco?ffici?nt' Yk afneemt bijtoenemende spreiding in de belasting, lijkt op het eerste ge-zicht onjuist. Bedacht moet echter worden dat Yk slechts demarge aangeeft tussende karakteristiekewaarden. De karakte-ristiekewaardevandebelasting(Sk) wordtechterzelfook gro~ter bij toenemende spreiding. Een toenemende spreidingheeft dus zowel invloed op Sk als op Yk' Kennelijk is het in be-paalde gevallen zo, dat de vergrotende invloed op SIchet wint,met als gevolg dat Yk daalt.De invloed van de spreiding in de belastingop de bezwijkkansis bij VR = 0,15 volledig bepaald door de invloed op de karak-teristieke belasting (Yk onafhankelijk van Vs)'De veel gehoorde mening dat de veiligheidsco?ffici?nt (be-doeld wordt dan Yk of Ys respectievelijk yJ groter moet wor-den bij toenemende spreiding blijkt dus op een misverstandteberusten.Zou de centrale veiligheidsco?ffici?nt worden beschouwd,danzou blijkendat deze altijd stijgtbij toenemende spreiding.Dit houdt ook in dat de centrale veiligheidsfactor de meestelegante factor is om de veiligheid te defini?ren, omdat dezeniet op een'onlogische' wijze kanfluctueren met de spreiding.trische verdelingen. Veranderlijke belastingen worden beterbenaderd door een Gumbel-verdeling, terwijl voor de mate-rialen beter van een lognormale verdeling ofWeibull-verde~ling kan worden uitgegaan.In figuur 3 zijn een normale, een Gumbel- en een lognormale .verdeling geschetst (zie bijvoorbeeld CUR-rapport 109).Hetverschil meteennormaleverdeling is datde Gumbel-ver-deling aan de rechterkant een langere, en de lognormale- enWeibull-verdelingaandelinkerkanteenkortere 'staart'bezit-ten. Zoals zal blijken kan dit een grote invloed hebben op deveiligheidsfactoren.Dat het uitsluitend hanteren van normale verdelingen totproblemen kan leiden, moge volgen uit figuur 4, waarin voorf3 = 3,6 en Vs = 0,4 de vereiste ligging van de verdelingen isgegeven voor VR = 0,1 ? 0,3. Bij groter wordende spreidingneemt Yk sterk toe om bij VR = 0,28 zelfs oneindig teworden.Dit wordt veroorzaakt door de lange staart van de normaleverdeling van de sterkte, die in werkelijkheid niet bestaat.Veiligheidifactoren bij verschillende verdelingenEvenals ditin hetvoorgaande is gedaanvoor normaalverdeel-de belasting en sterkte, kunnen voor elke andere combinatievan verdelingen formules worden afgeleid voor de verschil-lende veiligheidsmarges. Hierbij moet gebruik worden ge-maakt van de zogenaamde convolutie-integraal, die nume-riek moet worden ge?ntegreerd.Voor deze integraal geldt:waann:Fs is de cumulatieve verdelingsfunctie van de belasting;.fa is de kansdichtheidsfunctie van de materiaalsterkte.Veiligheidsfactoren bij verschillende verdelingenTypen verdelingIn het voorgaande zijn formules voor veiligheidsfactoren af-geleid, uitgaande van normale verdelingen voor de belastingen de sterkte. In werkelijkheid gelden echter veelal asymme-P(Z